Download 6-6 p444 1-4 7

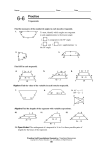
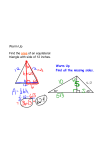
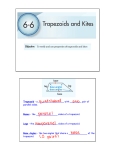
6-6 Trapezoids and Kites
Find each measure.
1. SOLUTION: The trapezoid ABCD is an isosceles trapezoid. So, each pair of base angles is congruent. Therefore,
2. WT, if ZX = 20 and TY = 15
SOLUTION: The trapezoid WXYZ is an isosceles trapezoid. So, the diagonals are congruent. Therefore, WY = ZX.
WT + TY = ZX
WT + 15 = 20
WT = 5
COORDINATE GEOMETRY Quadrilateral ABCD has vertices A (–4, –1), B(–2, 3), C(3, 3), and D(5, –1).
3. Verify that ABCD is a trapezoid.
SOLUTION: First graph the points on a coordinate grid and draw the trapezoid.
Use the slope formula to find the slope of the sides of the trapezoid.
eSolutions Manual - Powered by Cognero
Page 1
The slopes of exactly one pair of opposite sides are equal. So, they are parallel. Therefore, the quadrilateral ABCD is
a trapezoid.
SOLUTION: The trapezoid WXYZ is an isosceles trapezoid. So, the diagonals are congruent. Therefore, WY = ZX.
WT + TY = ZX
WT + 15 = 20and Kites
6-6 Trapezoids
WT = 5
COORDINATE GEOMETRY Quadrilateral ABCD has vertices A (–4, –1), B(–2, 3), C(3, 3), and D(5, –1).
3. Verify that ABCD is a trapezoid.
SOLUTION: First graph the points on a coordinate grid and draw the trapezoid.
Use the slope formula to find the slope of the sides of the trapezoid.
The slopes of exactly one pair of opposite sides are equal. So, they are parallel. Therefore, the quadrilateral ABCD is
a trapezoid.
4. Determine whether ABCD is an isosceles trapezoid. Explain.
SOLUTION: Refer to the graph of the trapezoid.
Use the slope formula to find the slope of the sides of the quadrilateral.
eSolutions Manual - Powered by Cognero
Page 2
The slopes of exactly one pair of opposite sides are equal. So, they are parallel. Therefore, the quadrilateral ABCD is
a trapezoid.
The slopes of exactly one pair of opposite sides are equal. So, they are parallel. Therefore, the quadrilateral ABCD is
6-6 Trapezoids
a trapezoid. and Kites
4. Determine whether ABCD is an isosceles trapezoid. Explain.
SOLUTION: Refer to the graph of the trapezoid.
Use the slope formula to find the slope of the sides of the quadrilateral.
The slopes of exactly one pair of opposite sides are equal. So, they are parallel. Therefore, the quadrilateral ABCD is
a trapezoid.
Use the Distance Formula to find the lengths of the legs of the trapezoid.
The lengths of the legs are equal. Therefore, ABCD is an isosceles trapezoid.
CCSS SENSE-MAKING If ABCD is a kite, find each measure.
7. SOLUTION: ∠A is an obtuse angle and ∠C is an acute angle. Since a kite can only have one pair of opposite congruent
angles and
The sum of the measures of the angles of a quadrilateral is 360.
eSolutions Manual - Powered by Cognero
Page 3
6-6 Trapezoids and Kites
The lengths of the legs are equal. Therefore, ABCD is an isosceles trapezoid.
CCSS SENSE-MAKING If ABCD is a kite, find each measure.
7. SOLUTION: ∠A is an obtuse angle and ∠C is an acute angle. Since a kite can only have one pair of opposite congruent
angles and
The sum of the measures of the angles of a quadrilateral is 360.
Find each measure.
9. SOLUTION: The trapezoid QRST is an isosceles trapezoid so each pair of base angles is congruent. So,
The sum of the measures of the angles of a quadrilateral is 360.
Let m∠Q = m∠T = x.
So,
11. PW, if XZ = 18 and PY = 3
eSolutions Manual - Powered by Cognero
SOLUTION: Page 4
6-6 Trapezoids
and Kites
So,
11. PW, if XZ = 18 and PY = 3
SOLUTION: The trapezoid WXYZ is an isosceles trapezoid. So, the diagonals are congruent. Therefore, YW = XZ.
YP + PW = XZ.
3 + PW = 18
PW = 15
COORDINATE GEOMETRY For each quadrilateral with the given vertices, verify that the quadrilateral
is a trapezoid and determine whether the figure is an isosceles trapezoid.
13. J(–4, –6), K(6, 2), L(1, 3), M (–4, –1)
SOLUTION: First graph the trapezoid.
Use the slope formula to find the slope of the sides of the quadrilateral.
The slopes of exactly one pair of opposite sides are equal. So, they are parallel. Therefore, the quadrilateral JKLM is
a trapezoid.
Use the Distance Formula to find the lengths of the legs of the trapezoid.
The lengths of the legs are not equal. Therefore, JKLM is not an isosceles trapezoid.
eSolutions Manual - Powered by Cognero
15. W(–5, –1), X(–2, 2), Y(3, 1), Z(5, –3)
SOLUTION: Page 5
SOLUTION: The trapezoid WXYZ is an isosceles trapezoid. So, the diagonals are congruent. Therefore, YW = XZ.
YP + PW = XZ.
3 + PW = 18and Kites
6-6 Trapezoids
PW = 15
COORDINATE GEOMETRY For each quadrilateral with the given vertices, verify that the quadrilateral
is a trapezoid and determine whether the figure is an isosceles trapezoid.
13. J(–4, –6), K(6, 2), L(1, 3), M (–4, –1)
SOLUTION: First graph the trapezoid.
Use the slope formula to find the slope of the sides of the quadrilateral.
The slopes of exactly one pair of opposite sides are equal. So, they are parallel. Therefore, the quadrilateral JKLM is
a trapezoid.
Use the Distance Formula to find the lengths of the legs of the trapezoid.
The lengths of the legs are not equal. Therefore, JKLM is not an isosceles trapezoid.
15. W(–5, –1), X(–2, 2), Y(3, 1), Z(5, –3)
SOLUTION: First graph the trapezoid.
eSolutions
- Powered
by Cognero
Use Manual
the slope
formula
to find
the slope of the sides of the quadrilateral.
Page 6
6-6 Trapezoids
and
The lengths of
theKites
legs are not equal. Therefore, JKLM is not an isosceles trapezoid.
15. W(–5, –1), X(–2, 2), Y(3, 1), Z(5, –3)
SOLUTION: First graph the trapezoid.
Use the slope formula to find the slope of the sides of the quadrilateral.
The slopes of exactly one pair of opposite sides are equal. So, they are parallel. Therefore, the quadrilateral WXYZ is
a trapezoid.
Use the Distance Formula to find the lengths of the legs of the trapezoid.
The lengths of the legs are not equal. Therefore, WXYZ is not an isosceles trapezoid.
For trapezoid QRTU, V and S are midpoints of the legs.
17. If QR = 4 and UT = 16, find VS.
SOLUTION: By the Trapezoid Midsegment Theorem, the midsegment of a trapezoid is parallel to each base and its measure is
one half the sum of the lengths of the bases.
are the bases and is the midsegment. So,
eSolutions Manual - Powered by Cognero
Page 7
6-6 Trapezoids and Kites
The lengths of the legs are not equal. Therefore, WXYZ is not an isosceles trapezoid.
For trapezoid QRTU, V and S are midpoints of the legs.
17. If QR = 4 and UT = 16, find VS.
SOLUTION: By the Trapezoid Midsegment Theorem, the midsegment of a trapezoid is parallel to each base and its measure is
one half the sum of the lengths of the bases.
are the bases and is the midsegment. So,
19. If TU = 26 and SV = 17, find QR.
SOLUTION: By the Trapezoid Midsegment Theorem, the midsegment of a trapezoid is parallel to each base and its measure is
one half the sum of the lengths of the bases.
are the bases and is the midsegment. So,
21. If RQ = 5 and VS = 11, find UT.
SOLUTION: By the Trapezoid Midsegment Theorem, the midsegment of a trapezoid is parallel to each base and its measure is
one half the sum of the lengths of the bases.
are the bases and is the midsegment. So,
eSolutions Manual - Powered by Cognero
Page 8