Download 32.1. Solve - Northern Highlands

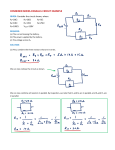
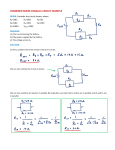
32.1. Solve:
From the circuit in Figure EX32.1, we see that 50 Ω and 100 Ω resistors are connected in series across the
battery. Another resistor of 75 Ω is also connected across the battery.
32.5. Model: Assume ideal connecting wires and an ideal battery for which ΔVbat = E .
Visualize: Please refer to Figure EX32.5. We will choose a clockwise direction for I. Note that the choice of
the current’s direction is arbitrary because, with two batteries, we may not be sure of the actual current direction.
The 3 V battery will be labeled 1 and the 6 V battery will be labeled 2.
Solve: (a) Kirchhoff’s loop law, going clockwise from the negative terminal of the 3-V battery is
ΔVclosed loop = ∑ ( ΔV )i = ΔVbat 1 + ΔVR + ΔVbat 2 = 0
i
⇒ +3 V – (18 Ω) I + 6 V = 0 ⇒ I =
9V
= 0.5 A
18 Ω
Thus, the current through the 18 Ω resistor is 0.5 A. Because I is positive, the current is left to right (i.e., clockwise).
(b)
Assess: The graph shows a 3 V gain in battery 1, a −9 V loss in the resistor, and a gain of 6 V in battery 2. The
final potential is the same as the initial potential, as required.
32.9. Model: The 100 W rating is for operating at 120 V.
Solve: A standard bulb uses ΔV = 120 V. We can use the power dissipation to find the resistance of the
filament:
ΔV 2
ΔV 2 (120 V )
⇒ R=
=
= 144 Ω
P
100 W
R
2
P=
But the resistance is related to the filament’s geometry:
R=
ρL
A
=
ρL
ρL
=
⇒ r=
2
πr
πR
The filament’s diameter is d = 2r = 23.6 μm.
( 9.0 × 10
−7
Ω m ) ( 0.070 m )
π (144 Ω )
= 1.18 × 10−5 m = 11.8 μ m
32.11. Solve: (a) The average power consumed by a typical American family is
Pavg = 1000
kWh
kWh
1000
= 1000
=
kW = 1.389 kW
month
30 × 24 h 720
Because P = (ΔV )I with ΔV as the voltage of the power line to the house,
I avg =
Pavg
ΔV
=
1.389 kW 1389 W
=
= 11.6 A
120 V
120 V
(b) Because P = ( ΔV ) /R,
2
Ravg =
( ΔV )
Pavg
2
=
(120 V )
1389 W
2
= 10.4 Ω
32.15. Model: Assume ideal connecting wires and an ideal power supply.
Visualize:
The two light bulbs are basically two resistors in series.
Solve: A 75 W (120 V) light bulb has a resistance of
ΔV 2 (120 V )
=
= 192 Ω
P
75 W
2
R=
The combined resistance of the two bulbs is
Req = R1 + R2 = 192 Ω + 192 Ω = 384 Ω
The current I flowing through Req is
I=
ΔV 120 V
=
= 0.3125 A
Req 384 Ω
Because Req is a series combination of R1 and R2, the current 0.3125 A flows through R1 and R2. Thus,
PR1 = I2R1 = (0.3125 A)2(192 Ω) = 18.8 W = PR2
32.17. Model: Assume ideal connecting wires and an ideal ammeter but not an ideal battery.
Visualize: Please refer to Figure EX32.17.
Solve: An ideal ammeter has zero resistance, so the battery is being short circuited. If I is the current flowing
through the circuit, then
I=
E
E 1.5 V
⇒ r= =
= 0.65 Ω
r
I 2.3 A
The power dissipated by the internal resistance is
P = I2r = (2.3 A)2(0.6522 Ω) = 3.5 W
32.21. Visualize: The three resistors in Figure EX32.21 are equivalent to a resistor of resistance Req = 75 Ω.
Solve:
Because the three resistors are in parallel,
1
1
1
1 2
1
400 Ω + R
( 200 Ω ) R =
⇒ Req = 75 Ω =
= +
+ = +
=
Req R 200 Ω R R 200 Ω ( 200 Ω ) R
( 400 Ω + R )
⇒R=
400 Ω
= 240 Ω
200 Ω
−1
75 Ω
200 Ω
⎛ 400 Ω ⎞
1+ ⎜
⎟
⎝ R ⎠
32.23. Model: The connecting wires are ideal with zero resistance.
Solve:
For the first step, the 10 Ω and 30 Ω resistors are in series and the equivalent resistance is 40 Ω. For the second
step, the 60 Ω and 40 Ω resistors are in parallel and the equivalent resistance is
−1
1 ⎤
⎡ 1
⎢ 40 Ω + 60 Ω ⎥ = 24 Ω
⎣
⎦
For the third step, the 24 Ω and 10 Ω resistors are in series and the equivalent resistance is 34 Ω.
32.25. Model: The connecting wires are ideal with zero resistance.
Solve:
In the first step, the resistors 100 Ω, 100 Ω, and 100 Ω in the top branch are in series. Their combined resistance
is 300 Ω. In the middle branch, the two resistors, each 100 Ω, are in series. So, their equivalent resistance is 200
Ω. In the second step, the three resistors are in parallel. Their equivalent resistance is
1
1
1
1
⇒ Req = 54.5 Ω
=
+
+
Req 300 Ω 200 Ω 100 Ω
The equivalent resistance of the circuit is 54.5 Ω.
32.27. Model: Grounding does not affect a circuit’s behavior.
Visualize: Please refer to Figure EX32.27.
Solve: Because the earth has Vearth = 0 V, point d has a potential of zero. In going from point d to point a, the
potential increases by 9 V. Thus, point a is at a potential of 9 V. Let us calculate the current I in the circuit before
calculating the potentials at points b and c. Applying Kirchhoff’s loop rule, starting clockwise from point d,
∑ ( ΔV )
i
i
= ΔV9 V bat + ΔV2 Ω + ΔV6 V bat + ΔV1 Ω = 0
⇒ +9 V – I(2 Ω) – 6 V – I(1 Ω) = 0 ⇒ I =
3V
=1 A
3Ω
There is a drop in potential from point a to point b by an amount IR = (1 A)(2 Ω) = 2 V. Thus, the potential at
point
b
is
9 V − 2 V = 7 V. The potential decreases from 7 V at point b to 7 V − 6 V = 1 V at point c. There is a further
decrease in potential across the 1 Ω resistor of IR = (1 A)(1 Ω) = 1 V. That is, the potential of 1 V at c becomes 0
V at point d, as it must. In summary, the potentials at a, b, c, and d are 9 V, 7 V, 1 V, and 0 V.
32.31. Model: Assume ideal wires as the capacitors discharge through the two 1 kΩ resistors.
Visualize: The circuit in Figure EX32.31 has an equivalent circuit with resistance Req and capacitance Ceq.
Solve: The equivalent capacitance is Ceq = 2 μF + 2 μF = 4 μF, and the equivalent resistance is
1
1
1
=
+
⇒ Req = 0.5 kΩ
Req 1 kΩ 1 kΩ
Thus, the time constant for the discharge of the capacitors is
τ = ReqCeq = (0.5 kΩ)(4 μF) = 2 × 10−3 s = 2 ms
32.35. Model: A capacitor discharges through a resistor. Assume ideal wires.
Solve: The discharge current or the resistor current follows Equation 32.35: I = I 0e− t RC . We wish to find the
capacitance C so that the resistor current will decrease to 25% of its initial value in 2.5 ms. That is,
0.25 I 0 = I 0e − 2.5 ms (100 Ω )C ⇒ ln ( 0.25 ) = −
2.5 × 10−3 s
⇒ C = 18.0 μF
(100 Ω ) C
32.41.
Visualize:
Solve:
(a) The three resistors in parallel have an equivalent resistance of
1
1
1
1
=
+
+
⇒ Req = 4.0 Ω
Req 12 Ω 12 Ω 12 Ω
(b) One resistor in parallel with two series resistors has an equivalent resistance of
1
1
1
1
1
1
⇒ Req = 8.0 Ω
=
+
=
+
=
Req 12 Ω + 12 Ω 12 Ω 24 Ω 12 Ω 8 Ω
(c) One resistor in series with two parallel resistors has an equivalent resistance of
−1
1
1 ⎞
⎛ 1
= 12 Ω + ⎜
+
⎟ = 12 Ω + 6 Ω = 18.0 Ω
Req
⎝ 12 Ω 12 Ω ⎠
(d) The three resistors in series have an equivalent resistance of
12 Ω + 12 Ω + 12 Ω = 36 Ω
32.43. Model: Assume the batteries and the connecting wires are ideal.
Visualize: Please refer to Figure P32.43.
Solve: (a) The two batteries in this circuit are oriented to “oppose” each other. The curent will flow in the
direction of the battery with the greater voltage. The direction of the current is counterclockwise because the 12
V battery is greater.
(b) There are no junctions, so the same current I flows through all circuit elements. Applying Kirchhoff’s loop
law in the counterclockwise direction and starting at the lower right corner,
∑ΔVi = 12 V − I(12 Ω) − I(6 Ω) − 6 V – IR = 0
Note that the IR terms are all negative because we’re applying the loop law in the direction of current flow, and
the potential decreases as current flows through a resistor. We can easily solve to find the unknown resistance R:
6 V − I(18 Ω) – IR = 0 ⇒ R =
6 V − (18 Ω ) I 6 V − (18 Ω )( 0.25 A )
=
=6Ω
0.25 A
I
(c) The power is P = I2R = (0.25 A)2(6 Ω) = 0.38 W.
(d)
The potential difference across a resistor is ΔV = IR, giving ΔV6 = 1.5 V, and ΔV12 = 3 V. Starting from the lower
left corner, the graph goes around the circuit clockwise, opposite from the direction in which we applied the loop
law. In this direction, we speak of potential as lost in the batteries and gained in the resistors.
32.47. Model: Assume that the connecting wire and the battery are ideal.
Visualize: Please refer to Figure P32.47.
Solve: The middle and right branches are in parallel, so the potential difference across these two branches must
be the same. The currents are known, so these potential differences are
ΔVmiddle = (3.0 A)R = ΔVright = (2.0 A)(R + 10 Ω)
This is easily solved to give R = 20 Ω. The middle resistor R is connected directly across the battery, thus (for an
ideal battery, with no internal resistance) the potential difference ΔVmiddle equals the emf of the battery. That is
E = ΔVmiddle = (3.0 A)(20 Ω) = 60 V
32.51. Model: Assume an ideal battery and ideal connecting wires.
Visualize:
Solve: (a) Grounding one point doesn’t affect the basic analysis of the circuit. In Figure P32.51, there is a
single loop with a single current I flowing in the clockwise direction. Applying Kirchhoff’s loop law clockwise
from the lower right corner gives
12 V
= 0.50 A
24 Ω
Knowing the current, we can use ΔV = IR to find the potential difference across each resistor:
∑ΔVi = −8I + 12 V – 4I – 12I = 0 V ⇒ I =
ΔV8 = 4 V
ΔV4 = 2 V
ΔV12 = 6 V
The purpose of grounding one point in the circuit is to establish that point as the specific potential V = 0 V.
Grounding point d makes that potential there Vd = 0 V. Then we can use the known potential differences to find the
potential at other points in the circuit. Point a is 4 V less than point d (because potential decreases in the direction of
=
Vd
–
4
V
=
current
flow),
so
Va
–4 V. Point b is 12 V more than point a because of the battery. So Vb = Va + 12 V = 8 V. Point c is 2 V less than
point b, so Vc = Vb – 2 V = 6 V. Point d is 6 V less than point c, so Vd = Vc – 6 V = 0 V. This is a consistency
check—making one complete loop brings us back to the potential at which we started, namely 0 V.
(b) The information about the potentials is shown in the graph above.
(c) Moving the ground to point a doesn’t change the basic analysis of part (a) or the potential differences found
there. All that changes is that now Va = 0 V. Point b is 12 V more than point a because of the battery. So, Vb = Va
+ 12 V = 12 V. Point c is 2 V less than point b, so Vc = Vb – 2 V = 10 V. Point d is 6 V less than point c, so Vd =
Vc – 6 V = 4 V. Point a is 4 V less than point d, so Va = Vd – 4 V = 0 V. This brings us back to where we started.
The information about the potentials is shown in the graph above.
32.57. Model: The voltage source/battery and the connecting wires are ideal.
Visualize: Please refer to Figure P32.57.
Solve: Let us first apply Kirchhoff’s loop law starting clockwise from the lower left corner:
+Vin – IR – I (100 Ω) = 0 V ⇒ I =
Vin
R + 100 Ω
The output voltage is
Vin
Vout
100 Ω
⎛
⎞
Vout = (100 Ω ) I = (100 Ω ) ⎜
=
⎟⇒
R
100
+
Ω
V
R
+ 100 Ω
⎝
⎠
in
For Vout = Vin 10 , the above equation can be simplified to obtain R:
Vin 10
100 Ω
=
⇒ R + 100 Ω = 1000 Ω ⇒ R = 900 Ω
Vin
R + 100 Ω
32.61. Model: The battery and the connecting wires are ideal.
Visualize:
The figure shows how to simplify the circuit in Figure P32.61 using the laws of series and parallel resistances.
Having reduced the circuit to a single equivalent resistance, we will reverse the procedure and “build up” the
circuit using the loop law and the junction law to find the current and potential difference of each resistor.
Solve: From the last circuit in the diagram,
12 V
E
=
=2A
6Ω 6Ω
Thus, the current through the battery is 2 A. As we rebuild the circuit, we note that series resistors must have the
same current I and that parallel resistors must have the same potential difference ΔV.
I=
In Step 1, the 6 Ω resistor is returned to a 3 Ω and 3 Ω resistor in series. Both resistors must have the same 2 A
current as the 6 Ω resistance. We then use Ohm’s law to find
ΔV3 = (2 A)(3 Ω) = 6 V
As a check, 6 V + 6 V = 12 V, which was ΔV of the 6 Ω resistor. In Step 2, one of the two 3 Ω resistances is
returned to the 4 Ω, 48 Ω, and 16 Ω resistors in parallel. The three resistors must have the same ΔV = 6 V. From
Ohm’s law,
I4 =
6V
= 1.5 A
4Ω
Resistor
3Ω
4Ω
48 Ω
16 Ω
I 48 =
6V 1
= A
48 Ω 8
Potential difference (V)
6
6
6
6
I16 =
6V 3
= A
16 Ω 8
Current (A)
2
1.5
1.2
3.8