Download Systems and Surroundings

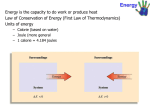
Lecture 5 Thermochemistry
Text: Fundamentals A.2, A.3, and Chapter 6
I. The Nature of Energy
energy, work, and heat
Thermodynamics: thermos ’hot’; dynamic 'powerful’
Energy is the capacity to do work or transfer heat.
Heat is energy transferred from a hotter object to a colder one.
Work - force applied by one object through a distance on another object.
(“work by something on something”)
w  F d
Systems and Surroundings
system – collection of objects that we study
surroundings - everything else
open system - can exchange energy and matter with surroundings.
closed system - can exchange energy but not matter with surroundings.
isolated system - can exchange neither energy nor matter with surroundings.
Energy can be exchanged with the surroundings as heat or work.
Chapter 5 Thermochemistry 1
Total Energy = Kinetic Energy + Potential Energy
Kinetic energy is the energy of motion. It depend on the mass, m, and velocity, v, of an object.
Ek 
1 2
mv
2
Potential energy P.E. is due to the position of one object relative to other objects. It is "stored
energy" that results from attraction or repulsion.
Gravitational P.E. = mgh (mass m of an object at height h, acceleration of gravity g = 9.8 m/s2)
Coulomb P.E. = co Q1Q2 (co constant, Q=charge, d=distance between particles 1 and 2)
d
PE of oppositely charged ions, N-S magnets, etc.
Chemical energy is due to the potential energy stored in the arrangement of the atoms of the
substance.
2 Fe + O2  2 FeO
Units of Energy
SI: Joule, 1 J = 1 kg m2/s2
calorie, 1 cal = 4.184 J (exactly)
Nutritional calorie, 1 Cal = 1000 cal = 1 kcal
Transferring Energy: Work and Heat
force - any kind of push or pull on an object.
Chapter 5 Thermochemistry 2
Internal Energy, U, - sum of all kinetic and potential energy of all components of the system.
(translational, rotational, vibrational, electronic, nuclear)
We can not measure all of these components at once, but we can measure changes.
“Change in U”,
U  Ufinal  Uinitial
Thermodynamic quantities have three parts:
sign (+ or –), number, unit (e.g. “+1.3 J” or “-0.5 kcal)
The + sign in ∆E means Ef > Ei
The system gained E from surroundings
The - sign in ∆E means Ef < Ei
The system lost E to surroundings.
The arrow head indicates the “final” point.
“Energy Diagram”
Relating ∆U to Heat and Work
U = q + w
Heat added to the system and work done on the system increase its internal energy.
Chapter 5 Thermochemistry 3
Sur roundings
q>0
in
Heat
out q<0
Syste m
w>0
out
in
w<0
Work
II. The Measurement of Work and Heat
A. The Measurement of Work
Table 6.1 lists several varieties of work, but one type of work, expansion work, can serve as an
example of how work is measured. Expansion work involves the change in volume, V, of a
system such as a gas inside a cylinder whose piston is held in place by an expernal pressure, Pex.
The amount of work is proportional to Pex X V but can vary according to how the pressure
changes. Pressure is the force exerted on the piston divided by the area of the piston (P =F/A).
There are several units for pressure. The one we will use in this discussion is atmosphere (atm). 1
atm (atmosphere) = 14.7 psi (pounds per square inch).
Suppose the piston exerts 3.00 atm and the volume inside the piston is found to be 8.00 L. If
some of the pressure on the piston is reduced, the volume of the gas will expand. Since the gas
Chapter 5 Thermochemistry 4
(the ‘system’) expands against the surroundings, the system does work on the surroundings. The
value of the work, w, is negative since the system becomes more stable. (See energy diagram.)
The external pressure can be changed in many ways. Each way will involve a different amount
of work. We shall look at two ways, each of which has its own formula for calculating the work.
1) Constant external pressure, Pex
This is path B in the diagram below. In a first step, the volume is held constant by keeping the
piston in place while adjusting the Pex from 3.00 atm to 1.2 atm. Then in a second step the piston
is released and allowed to expand against a constant Pex = 1.2 atm.
The work corresponds to the area under the path in the graph. Here it is simply a rectangle.
W = - Pex · V
When a gas expands against the surroundings, it loses energy in the form of work; the gas
becomes more stable. The negative sign shows the downward direction on the energy diagram.
Since both Pex and V are positive, there must be a negative sign in the formula.
Example: Calculate the work in kJ when a gas expands from 8.00 L to 20.00 L against a constant
pressure of 1.20 atm. ( 1 L·atm = 101.325 J)
W = - Pex · V = - 1.20 atm · ( 20.00 - 8.00 L) · 101.325 J/ L·atm · 1 kJ/1000 J = -1.46 kJ
Chapter 5 Thermochemistry 5
There is another way in which we can change the constant Pex and arrive at another amount of
work. As before, the first step consists of holding the piston in place so the volume remains at
8.00 L but this time we reduce the Pex to zero. The second step consists of letting the piston
expand against a vacuum and stopping the piston at 20.00 L. Then in a third step, the Pex is readjusted to 1.20 atm. In this case the work done by the gas against the surroundings is zero.
W = - Pex · V = - 0 atm · ( 20.00 - 8.00 L) = 0 L·atm = 0 J
The area under the graph is zero:
2) Changing external pressure Pex
A particular case is path A in the diagram below. Here the Pex is lowered infinitely slowly, point
by point. This point-by-point method is called a “reversible” process and permits us to calculate
the area under the curve using calculus. We will see the formula derived for reversible changes
later, after we study gases. At this point, the idealized “reversible” process is mentioned because
Chapter 5 Thermochemistry 6
it is a measure of the maximum work that can be obtained when a gas expands. Note the areas
under the curves.
Ideally, the Pex is reduced in infinitely small steps in the “reversible” method. Each one of the
(Pex · V) boxes would be an infinitely thin line under a point on the line. Calculus gives us a
mathematical way of counting an infinite number of infinitely thin lines to give an area.
Really, the Pex is reduced in finite steps as in the above figure and the area is the sum of the
boxes. This is called an “irreversible” method.
In summary,
i)
the work by the system in expanding (or contracting) against the surroundings is
measured by -Pex X V.
Chapter 5 Thermochemistry 7
ii)
the amount of work by the system on the surroundings varies according to how one
goes from point (Pinitial,V initial) to (Pfinal,Vfinal).
iii)
The amount can vary between zero for expansion against a vacuum to a maximum for
a “reversible” expansion.
The pressure of a gas can also be changed is by heating or cooling it. Temperature, T, is a
measure of the amount of heat available to an object. Another way is to change the amount of
gas, the number of moles, n. The product P·V is thus proportional to both T and n:
P·V α T
P·V α n
P·V α n·T
The proportionality sign  can be replaced by an equal sign and proportionality constant, R,
called the “gas constant”.
P·V = n R T
This relationship will be explored in detail in the next Lecture, but for now, we can see that units
of work, P·V can be related to units of heat, RT for gases. They are interrelated forms of energy.
U = w + q
B. The Measurement of Heat
Endothermic and Exothermic Processes
Endothermic - system absorbs heat; heat flows into system from surroundings. q>0
Exothermic - system evolves heat. Heat flows out of system and into surroundings. q<0
The Heat Capacity, C is the ratio of the heat needed to raise the temperature of an object.
C = q / T
or
q = C · T
Chapter 5 Thermochemistry 8
It is an extensive property in that the larger the sample, the more heat is required for the same
temperature rise. In order to have the same value for a particular substance no matter what the
amount, values are reported for either the
1) specific heat capacity, Cs per gram (m) of the substance, C = m·Cs
2) molar heat capacity, Cm per mole (n) of the substance, C = n·Cm
Calorimetry (L. calorem, heat G. - , measure)
Originally, 1 calorie cal was defined as the energy needed to raise the temperature of 1 g of
water by 1oC. The modern definition is
1 cal = 4.184 J (exactly)
It was postulated that the amount of heat lost by one object equaled exactly the amount gained by
the object that received the heat. Heat is not created or destroyed when it is transferred.
q, heat (to colder object) = - q, heat (from hotter object)
The sign is used to indicate direction of flow
If we hold this to be true, then we can use water to ‘jacket’ another object and the temperature
change, T of the water can be related to the T of the object by the definition of 1 cal = the heat
needed to raise 1 g of water by 1 oC.
Chapter 5 Thermochemistry 9
qwater = -qx
Cwater · Twater = Cx · Tx
m water · Cm water · Twater = m x · Cm x · Tx
m water · 1 (cal·g-1·oC-1) · Twater = m x · Cm x · Tx
m water · 4.184 (J·g-1·oC-1) · Twater = m x · Cm x · Tx
Self Tests 6.3,4B
Chapter 5 Thermochemistry 10
The First Law of Thermodynamics
End of Section One
Chapter 5 Thermochemistry 11