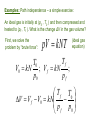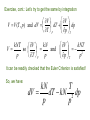* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download File 3 - College of Science | Oregon State University
Insulated glazing wikipedia , lookup
Internal energy wikipedia , lookup
Second law of thermodynamics wikipedia , lookup
Heat transfer physics wikipedia , lookup
Thermal expansion wikipedia , lookup
History of thermodynamics wikipedia , lookup
Adiabatic process wikipedia , lookup
Equation of state wikipedia , lookup
THERMODYNAMIC PROCESSES Uf Exact differentials: U dU U f U0 Regardless of path! U0 Another, equivalent criterion of exactness of dz : As we said, So, dz 0 and and are not exact differentials. EULER CRITERION: If dM A( x, y )dx B( x, y )dy M M dy dx x y y x is an exact differential, i.e., Then and only then: Based on the Euler Criterion are Maxwell Relations, a “family” of important identities in thermodynamics. dM 0 M M y x y x x y A B Meaning that: y x x y x y Also, the Euler Criterion is essential for introducing the notion of entropy! Another important formula, very often used in thermal physics, is the so-called “Cyclic Chain Rule”: Suppose that : M ( x, y ) const. Then dM 0 M M dy 0 dx x y y x By rearranging, we get: It is not the most elegant proof of this theorem – if you want a more “orthodox” proof, it can be found in math books (and a more general theory is the theory of “Jacobi Determinants”, a.k.a. “Jacobians” x y M M y M x x y Examples: Path independence – a simple exercise: An ideal gas is initially at (p0 , T0 ) and then compressed and heated to (pf , Tf ). What is the change ΔV in the gas volume? First, we solve the problem by “brute force”: pV kNT (ideal gas equation) Tf T0 V0 kN ; V f kN ; p0 pf T f T0 V V f V0 kN p p 0 f Exercise, cont.: Let’s try to get the same by integration V V dp V V (T , p) and dV dT T p p T kNT kN V V so and p p T p V p kNT 2 p T It can be readily checked that the Euler Criterion is satisfied! So, we have: kN T dV dT kN 2 dp p p Let’s now integrate. First, along Path 1: from p0 to pf with T = const. = T0 then From T0 to Tf with p = const. = pf pf Tf dp kN V kNT0 2 dT p T0 p f p0 pf 1 kN T f T0 kNT0 2 p p0 p f T0 T0 T f T0 T f T0 kN kN p p p p p p 0 f f 0 f f Same as by “brute force” – OK! Try the other path: from T0 to Tf with p = p0 = const., then from p0 to pf with T= Tf = const.: Tf kN V dT p0 T0 pf dp p kNTf p 2 0 T f T0 T f T f T f T0 kN kN p p p p p p 0 0 f 0 0 f OK!!! ☺ Another important comment: there are some “standard” coefficients, or “response functions” characterizing materials. For the most often used materials, the values of those coefficients are given in many books. We have already discussed the heat capacities Cv and Cp that are such “response functions”. Let’s introduce more: 1 V p V T p 1 V T V p T Constant pressure (isobaric) volume expansitivity (a.k.a. “volume thermal expansion coefficient”). Isothermal compressibility The volume differential dV we have used may be expressed in terms of these coefficients: dV V p dT V T dp Next example: “Free expansion of gas into vacuum” – a Good illustration of the use of the “cyclic chain rule” The gas surges into the formerly evacuated space, and eventually comes to equilibrium, now occupying the entire container. The question: does the gas temperature change in such a process? Try the First Law: U Q W But Q=0 because the walls are thermally insulated, and W=0 because the gas did not do any work! So, ΔU=0. It does not tell us very much… Let’s consider the temperature as a function of the Internal energy U and volume V: T=T(U,V). Then: T T dT dU dV U V V U But dU=0, so T dT dV V U We don’t know the value of this derivative, but here the “cyclic chain rule” offers much help: U V T T U V U T V One of these derivatives we already know! Could you tell which one? Yes! You are right, it’s the constant volume heat capacity! U CV T V So, we only need to know the other derivative: For ideal monoatomic gas: So, 3 U kNT 2 U 0 !!! V T U V T (you have to trust me!) It means that ideal gas does not change its temperature in the free expansion proces!!! Can you explain, why? A more realistic gas model is the well-known Van der Waals gas with a state equation: 2 N pV kNT p a 2 V Nb kNT V Constants to be determined from experiments on a given gas The internal energy of van der Waals gas can be obtained From calculations that tare not trivial (so we will skip them): 2 U van der Waals N a CV T U0 V Undetermined integration constant Van der Waals gas vacuum expansion, cont.: From the energy equation, we get: U N a V T V 2 Inserting into the formula we got on Slide 10: U N a 2 aN V T V T CV CV V 2 U V U T V 2 So: aN 2 dT dV 2 CV V It is negative – the temperature decreases! We want to calculate the change of T in the process – but we cannot integrate dT without knowing how Cv depends on temperature. Again, Euler’s Criterion will help us to answer that question: U U N U U (T ,V ) dU dT dV C dT a dV V T V V T V 2 Because dU is for sure an exact differential (how do we know that?), we can apply the Euler Criterion to get: 2 N CV a V T T V Tf The right side is obviously zero, meaning that CV is not a function of V. So, the integration is straightforward: aN T dT CV T0 dV aN 1 1 V V 2 CV V f V0 0 2 Vf 2