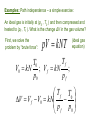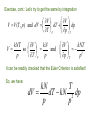Download File 3 - College of Science | Oregon State University

THERMODYNAMIC PROCESSES
Uf
Exact differentials:
U 
 dU  U
f
U0
Regardless
of path!
U0
Another, equivalent criterion of exactness of dz :
As we said,
So,
dz

0

and
and
are not exact differentials.
EULER CRITERION:
If dM  A( x, y )dx  B( x, y )dy
 M 
 M 
 dy

 dx  
 x  y
 y  x
is an exact differential, i.e.,
Then and
only then:
Based on the Euler
Criterion are Maxwell
Relations, a “family”
of important identities
in thermodynamics.
dM

0

   M      M
    
 
 y  x  y  x  x  y
 A   B 
Meaning that: 
 y    x 
 x   y
 
 
 x  y
Also, the Euler Criterion
is essential for introducing
the notion of entropy!
Another important formula, very often used in thermal
physics, is the so-called “Cyclic Chain Rule”:
Suppose that : M ( x, y ) const.
Then
dM  0
 M 
 M 
 dy
 0
 dx  
 x  y
 y  x
By rearranging, we get:
It is not the most elegant
proof of this theorem – if
you want a more “orthodox”
proof, it can be found in math
books (and a more general
theory is the theory of “Jacobi
Determinants”, a.k.a.
“Jacobians”
 x 
 
 y  M
 M

 y

 M

 x


x


y
Examples: Path independence – a simple exercise:
An ideal gas is initially at (p0 , T0 ) and then compressed and
heated to (pf , Tf ). What is the change ΔV in the gas volume?
First, we solve the
problem by “brute force”:
pV  kNT
(ideal gas
equation)
Tf
T0
V0  kN ; V f  kN
;
p0
pf
 T f T0 
V  V f  V0  kN 
 
p

p
0 
 f
Exercise, cont.: Let’s try to get the same by integration
 V 
 V 
 dp
V  V (T , p) and dV  
 dT  
 T  p
 p T
kNT
kN
 V 
V
so 
and
 
p
p
 T  p
 V

 p

kNT
   2
p
T
It can be readily checked that the Euler Criterion is satisfied!
So, we have:
kN
T
dV 
dT  kN 2 dp
p
p
Let’s now integrate.
First, along Path 1:
from p0 to pf with T = const. = T0
then
From T0 to Tf with p = const. = pf
pf
Tf
dp
kN
V    kNT0 2   dT
p T0 p f
p0
pf
 1 
kN
T f  T0 
 kNT0   2  
 p  p0 p f
 T0 T0 T f T0 
 T f T0 
  kN
 kN



 
p

p

p
p
p
p
0
f
f 
0 
 f
 f
Same as
by “brute
force” – OK!
Try the other path: from T0 to Tf with p = p0 = const.,
then from p0 to pf with T= Tf = const.:
Tf
kN
V   dT 
p0
T0
pf
dp
p  kNTf  p 2
0
 T f T0 T f T f 
 T f T0 
  kN 
 kN  


 
p

p

p
p
p
p
0
0
f 
0 
 0
 f
OK!!! ☺
Another important comment: there are some “standard”
coefficients, or “response functions” characterizing
materials. For the most often used materials, the values
of those coefficients are given in many books.
We have already discussed the heat capacities Cv and Cp
that are such “response functions”. Let’s introduce more:
1  V 
p  

V  T  p
1  V
 T   
V  p


T
Constant pressure (isobaric) volume
expansitivity (a.k.a. “volume thermal
expansion coefficient”).
Isothermal compressibility
The volume differential dV we have used may be expressed
in terms of these coefficients:
dV  V   p dT  V   T dp
Next example: “Free expansion of gas into vacuum” – a
Good illustration of the use of the “cyclic chain rule”
The gas surges into the formerly evacuated space, and
eventually comes to equilibrium, now occupying the entire
container. The question: does the gas temperature
change in such a process?
Try the First Law:
U  Q  W
But Q=0 because the walls are thermally insulated, and
W=0 because the gas did not do any work! So, ΔU=0. It
does not tell us very much…
Let’s consider the temperature as a function of the
Internal energy U and volume V: T=T(U,V). Then:
 T 
 T 
dT  
 dU  
 dV
 U V
 V U
But dU=0, so
 T 
dT  
 dV
 V U
We don’t know the value of this derivative, but here the
“cyclic chain rule” offers much help:
 U 


V T
 T 


 
 U 
 V U


 T V
One of these
derivatives we
already know!
Could you tell
which one?
Yes! You are right, it’s the constant volume heat capacity!
 U 

  CV
 T V
So, we only need to know the other derivative:
For ideal
monoatomic
gas:
So,
3
U  kNT
2
 U 

  0 !!!
 V T
 U 


 V T
(you have to
trust me!)
It means that ideal gas does not
change its temperature in the
free expansion proces!!!
Can you explain, why?
A more realistic gas model is the well-known
Van der Waals gas with a state equation:
2

N 
pV  kNT   p  a 2 V  Nb  kNT
V 

Constants to be determined from
experiments on a given gas
The internal energy of van der Waals gas can be obtained
From calculations that tare not trivial (so we will skip them):
2
U van der Waals
N a
 CV T 
U0
V
Undetermined integration
constant
Van der Waals gas vacuum expansion, cont.:
From the energy equation, we get:
 U 
N

  a 
 V T
V 
2
Inserting into the formula we got on Slide 10:
 U 
N
a 


2
aN
V T
V
 T 

   

 
CV
CV  V 2
 U 
 V U


 T V
2
So:
aN 2
dT  
dV
2
CV V
It is negative – the temperature
decreases!
We want to calculate the change of T in the process –
but we cannot integrate dT without knowing how Cv depends
on temperature.
Again, Euler’s Criterion will help us to answer that question:
 U 
 U 
N
U  U (T ,V )  dU  
dT

dV

C
dT

a



  dV
V
 T V
 V T
V 
2
Because dU is for sure an exact differential (how do we
know that?), we can apply the Euler Criterion to get:
2

 N 
 CV 

   a  
 V T  T  V  
Tf
The right side is obviously zero,
meaning that CV is not a function of V.
So, the integration is straightforward:
aN
T   dT  
CV
T0
dV aN  1
1 
V V 2  CV  V f  V0 


0
2 Vf
2