Download 7.1 - Systems of Linear Equations What is the solution of a line

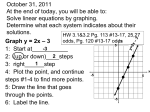
7.1 - Systems of Linear Equations
What is the solution of a line??
Solution of 2x + y = 5?
y
8
7
6
5
4
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1
0
-1
-2
-3
-4
-5
-6
-7
-8
1
2
3 4 5 6
7 8
x
System of Linear Equations:
2x + 3y = -1
-x + y = -3
OR
2x - 3y - z = 0
-x + 2y + z = 5
3x - 4y - z = 1
System of Equations - 2 or more equations, each containing 1 or
more variables
Is (2, 1 ) a solution for:
2x + y = 5
-4x + 6y = -2
Check:
Solution of a system - x, y (& z for 3 equations) values that
satisfy each equation of the system
To solve a system, must find all such solutions
System of linear equations is 2 (or 3) lines
Lines either:
1 ) Intersect
2) Parallel
3) Coincident (same line)
Possible solutions to a system:
1 ) one solution (intersect)
2) No solution (parallel)
3) Infinite # of solutions (coincident)
Consistent system - system that has at least one solution
Inconsistent system - system that has no solution
Dependent system - system where any solution of one equation is
a solution of the other
Independent system - system where solutions of one equation is
not necessarily a solution of the other equation
3 ways to solve:
1 ) Graphing
-graph each line and find point of intersection
2) Substitution
-solve for 1 variable in terms of the other in 1 equation
-substitute the result in the remaining equation and solve
-find value of remaining variable by back substitution
3) Elimination or Addition
-multiply each side of an equation(s) by the same nonzero
constant
-add the 2 equations to eliminate one of the variables
-solve for remaining variable
-use back substitution to solve for variable that was
eliminated
Graphing
Ex: Find each solution by graphing. State if the system is
consistent or inconsistent, and dependent or independent.
1 . 3x + 2y = 2
x - 7y = -30
y
10
9
8
7
6
2. x - y = 3
-3x + y = 1
5
4
3
2
1
-1 0 -9 -8 -7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
-7
-8
-9
-1 0
1
2
3
4
5
6
7
8
9 10
x
Substitution Method
Ex: Find each solution using substitution. State if the system
is consistent or inconsistent, and dependent or independent.
1 . x + 3y = 5
2x - 3y = -8
2. x - y = 5
-3x + 3y = 2
Elimination Method
Ex: Find solution using elimination. State if the system is
consistent or inconsistent, and dependent or independent.
1 . 3x + 3y = -1
4x + y = 8
3
2. 2x + 4y =
2
3
3x - 5y = -1 0