* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File
Penrose tiling wikipedia , lookup
Technical drawing wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
History of geometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Apollonian network wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
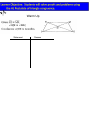
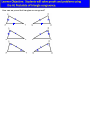
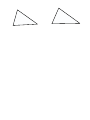
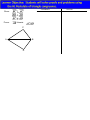
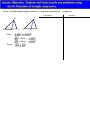
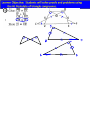
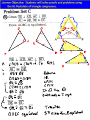
Advanced Geometry Section 3.8 The HL Postulate Learner Objective: Students will solve proofs and problems using the HL Postulate of triangle congruence. Warm Up Statement Reason How can we prove that triangles are congruent? What about SSA? In these triangles, two pairs of corresponding sides and a NON-INCLUDED pair of corresponding angles are congruent. Do the triangles appear to be congruent? There is one special case when SSA does prove triangles are congruent. This occurs when the corresponding angles are RIGHT ANGLES which makes the congruent sides a HYPOTENUSE and a LEG of the RIGHT triangle. H-L Postulate If there exists a correspondence between the vertices of two RIGHT TRIANGLES such that the Hypotenuse and a Leg of one triangle are congruent to the corresponding parts of the other triangle, then the two RIGHT TRIANGLES are congruent. ONLY APPLIES TO RIGHT TRIANGLES! STATEMENTS Given: Prove: bisects C B A D REASONS Prove: Corresponding angle bisectors of congruent triangles are congruent. STATEMENTS E B A G C D Given: bisects bisects Prove: H F REASONS HW: Pg. 158 # 1,2,6,7,10,12,15