Download Lesson 4.3 Graphing Other Trigonometric Functions notes

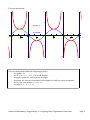
4.3 Graphing Other Trigonometric Functions
The tangent function:
f  x = tan  x
2
-5
-
3
2
-
-


2
2

3 5
2
2
-2
The tangent function exhibits the following properties:
- It’s period is 
- For all x, tan (-x) = - tan x. It is an odd function.
- Its graph is symmetric with respect to the origin.
𝜋
- Its domain: the tangent is undefined at all odd multiples of and has vertical asymptotes
𝜋
2
at every line with equation 𝑥 = (2𝑘 + 1) ; 𝑘 ∈ 𝑍
-
Its range is the set of all real numbers, .
Its zeros occur at multiples of .
2
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 1
The cotangent function:
f(x) = cot x
2
-2
-5
-
3
2
-
-


2
2

3 5
2
2
-2
The cotangent function exhibits the following properties:
- It’s period is 
- For all x, cot (-x) = - cot x. It is an odd function.
- Its graph is symmetric with respect to the origin.
- Its domain: the cotangent is undefined at all multiples of  and has vertical asymptotes
at every line with equation x  k ; k  Z
- Its range is the set of all real numbers, .
𝜋
- Its zeros occur at odd multiples of .
2
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 2
Example 1: Graph each function.
1
a. 𝑦 = tan 𝑥
2
y
6
5
4
3
2
1
-3
-
5
-2
2
-
3
-
2
-


2

2
-1
x
3
2
2
5
3
2
-2
-3
-4
-5
-6
1
b. 𝑦 = tan 𝑥
3
y
6
5
4
3
2
1
-3
-
5
2
-2
-
3
2
-
-


2
-1
2

x
3
2
2
5
3
2
-2
-3
-4
-5
-6
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 3
c. 𝑦 = tan 3𝑥
y
4
3
2
1
-

2
-

3
-

6
-1



6
3
2
x
-2
-3
-4
For the functions 𝑓(𝑥) = 𝑎 tan 𝑏(𝑥 − 𝑐) + 𝑑 and 𝑔(𝑥) = 𝑎 cot 𝑏(𝑥 − 𝑐) + 𝑑, the constants a, b, c, and d
affect the graphs. Since amplitude does not apply to these functions, a vertically dilates the graph, period is
𝜋
|𝑏|
, phase shift is |𝑐| (to the left if c < 0 and to the right if c > 0) and vertical shift is |𝑑| (downward if d < 0
and upward if d > 0).
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 4
Example 2: Determine the period, phase shift, vertical shift, and the equations of at least two vertical
asymptotes of each. Then graph.
𝜋
a. 𝑓(𝑥) = 2 tan (𝑥 − ) + 3
6
y
x
b. 𝑓(𝑥) = cot(2𝑥 − 𝜋)
y
x
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 5
Example 3: Derive an equation with the given characteristics then graph each.
a. cotangent: period
𝜋
2
, phase shift
𝜋
4
left
y
x
𝜋
𝜋
2
4
b. tangent: period , phase shift
left
y
x
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 6
The secant function:
y = sec x
2
y = cos x
-2
-5
-
3
-
2
-


2

2
3
5
2
2
-2
-4
The secant function exhibits the following properties:
- It’s period is 2
- For all x, sec (-x) = sec x. It is an even function.
- Its graph is symmetric with respect to the y-axis.
𝜋
- Its domain: the secant is undefined at all odd multiples of and has vertical asymptotes
𝜋
2
at every line with equation 𝑥 = (2𝑘 + 1) ; 𝑘 ∈ 𝑍
-
Its range is (-, -1]  [1, )
2
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 7
The cosecant function:
4
2
y= csc x
y = sin x
-2
-5
-
3
2
-
-


2
2

3
5
2
2
-2
-4
The cosecant function exhibits the following properties:
- It’s period is 2
- For all x, csc (-x) = - csc x. It is an odd function.
- Its graph is symmetric with respect to the origin.
- Its domain: the cosecant is undefined at all multiples of  and has vertical asymptotes
at every line with equation x  k ; k  Z
- Its range is (-, -1]  [1, )
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 8
Example 4: Graph each function.
1
a. 𝑦 = −2 sec 𝑥
2
y
x
1
b. 𝑦 = 4 sec 𝑥
4
y
x
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 9
1
c. 𝑦 = csc 3𝑥
2
y
x
For the functions 𝑓(𝑥) = 𝑎 sec 𝑏(𝑥 − 𝑐) + 𝑑 and 𝑔(𝑥) = 𝑎 csc 𝑏(𝑥 − 𝑐) + 𝑑 , the constants a, b, c, and d
affect the graphs. Since amplitude does not apply to these functions, a vertically dilates the graph, period is
2𝜋
|𝑏|
, phase shift is |𝑐| (to the left if c < 0 and to the right if c > 0) and vertical shift is |𝑑| (downward if d < 0
and upward if d > 0).
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 10
Example 5: Find the period, phase shift, vertical shift, and the equations of at least two vertical asymptotes
of each. Then graph.
a. 𝑦 = csc (4𝑥 +
3𝜋
2
)−1
y
x
b. 𝑦 = sec(2𝑥 − 𝜋) + 2
y
x
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 11
Homework: pp. 205 – 206: Practice Exercises 1, 4, 7, 8, 10, 12, 14, 17, 19 (day 1)
pp. 206 – 207: Practice Exercises 21 – 23; 34, 37, 39 (day 2)
pp. 205 – 207: Practice Exercises 11, 13, 15, 35 (day 3)
pp. 205 – 207: Practice Exercises 2, 3, 5, 36, 38 (day 4)
Advanced Mathematics/Trigonometry: 4.3 Graphing Other Trigonometric Functions
Page 12