Download Dilations Intro.

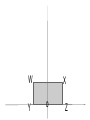
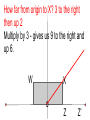
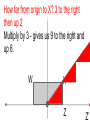
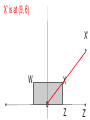
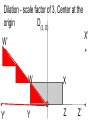
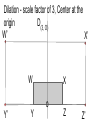
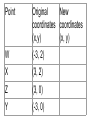
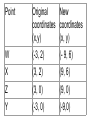
12 Nov 2016 8 - 9:30 AM
Geometry Agenda
Bulletin
Dilations - New work
Homework
Unit 2B Test
11/12/2016
Dilations
i
ations
A Dilation is a transformation
that creates a similar shape.
(not congruent)
Dilations
i
ations
A similar shape is a shape
whose angles are congruent
and has proportional sides.
(If one side gets 4 times bigger, all the
sides do, or half as big etc. - constant
scale factor.)
The picture below displays a
dilation that maps triangle ABC
to triangle A’B’C’. Since the
new triangle is twice as big and
it is being dilated with a center
point 0, it would be
represented as
D(2,0)
△ABC →△A’B’C’
A’
A
C
C’
B
B’
Most dilations that we will do
will have a center of the origin.
We will do a dilation below
using the rectangle WXYZ.
(How should the rectangle be
labeled? Never mind.)
W
Y
X
o
Z
Dilation - scale factor of 3, Center at the
origin
D(3, O)
How far
from origin
to Z?
o
Z
Z’
Dilation - scale factor of 3, Center at the
origin
D(3, O)
3 units,
3x3
=
9
units
o
Z
How far from origin to X? 3 to the right
then up 2
Multiply by 3 - gives us 9 to the right and
up 6.
W
X
o
Z
Z’
How far from origin to X? 3 to the right
then up 2
Multiply by 3 - gives us 9 to the right and
up 6.
W
X
o
Z
X’ is at (9, 6)
X’
W
X
o
Z
Z’
Dilation - scale factor of 3, Center at the
origin
D(3, O)
X’
W’
W
X
o
Y’
Y
Z
Z’
Dilation - scale factor of 3, Center at the
origin
D(3, O)
W’
X’
W
X
o
Y’
Y
Z
Z’
Point
Original
New
coordinates coordinates
(x,y)
(x, y)
W
(-3, 2)
X
(3, 2)
Z
(3, 0)
Y
(-3, 0)
Point
Original
New
coordinates coordinates
(x,y)
(x, y)
W
(-3, 2)
(- 9, 6)
X
(3, 2)
(9, 6)
Z
(3, 0)
(9, 0)
Y
(-3, 0)
(-9,0)
What do you notice about the
relationship between the
original points and the points
after the dilation?
I notice that the original points,
with coordinates (x, y), become
points (3x, 3y) after the dilation
with a scale factor of 3 with a
center of dilation at the origin.
If I represent the scale factor as
a real number, r, then for any
point P(x, y) it will become
P’(rx, ry) after a dilation with a
center at the origin.
2) On the graph below plot the three points
A(3, 2), B (-2, -3), and C (-4, 1).
A(3, 2) → A’
B (-2, -3)→ B’
C (-4, 1)→C’
3) Perform the following dilation on the
triangle above D(2, O). Plot the new points
A(3, 2) → A’ (6, 4)
scale factor is 2
B (-2, -3)→ B’
C (-4, 1)→ C’
3) Perform the following dilation on the
triangle above D(2, O). Plot the new points
A(3, 2) → A’ (6, 4)
scale factor is 2
B (-2, -3)→ B’ (-4, -6)
C (-4, 1)→ C’
3) Perform the following dilation on the
triangle above D(2, O). Plot the new points
A(3, 2) → A’ (6, 4)
scale factor is 2
B (-2, -3)→ B’ (-4, -6)
C (-4, 1)→ C’ (-8, 2)
3) Perform the following dilation on the
triangle above D(2, O). Plot the new points
4) On the graph below plot the three points
D(6, 2), B (-2, -4), and C (-4, 6).
D(6, 2) → D’ right 6 up 2,
B (-2, -4) → B’
C (-4, 6) → C’
5) Perform the following dilation on the
triangle above D(1/2, O). Plot the new points.
D(6, 2) → D’ (3, 1)
Scale factor is ½
B (-2, -4) → B’
C (-4, 6) → C’
5) Perform the following dilation on the
triangle above D(1/2, O). Plot the new points
D(6, 2) → D’ (3, 1)
Scale factor is ½
B (-2, -4) → B’ (-1, -2)
C (-4, 6) → C’
D(6, 2) → D’ (3, 1)
Scale factor is ½
B (-2, -4) → B’ (-1, -2)
C (-4, 6) → C’ (-2, 3)
What’s happened to the size of the triangle?
Homework Due: Monday, November 14.
Dilations Homework Worksheet (pg 3-4)
Qu. 1 - 6
Label all diagrams; Write the points and points’
in the space to the right of the graphs.
Lesson 1 Dilations Extra Practice pg 5
Try 1 and 2 on your own. (Hint. Count squares
from the center of dilation.)
Geometry - Unit 2BTest
Cell phones turned off and away in your backpacks Calculators OK
Pen or pencil
Show all your work.
Turn in the Review Parts 1& 2 sheet before we start
test.