Download Chapter 25

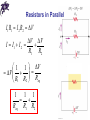
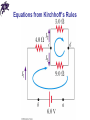
Chapter 25
Electric Circuits
Direct Current
• When the current in a circuit has a constant direction,
the current is called direct current
• Most of the circuits analyzed will be assumed to be in
steady state, with constant magnitude and direction
• Because the potential difference between the terminals
of a battery is constant, the battery produces direct
current
• The battery is known as a source of emf
Sources of emf
• The source that maintains the current in a closed
circuit is called a source of emf
• Any devices that increase the potential energy of
charges circulating in circuits are sources of emf (e.g.
batteries, generators, etc.)
• The emf (ε) is the work done per unit charge
• Emf of a source is the maximum possible voltage that
the source can provide between its terminals
• SI units: Volts
Electric Circuits
• A circuit is a collection of objects usually containing a
source of electrical energy connected to elements that
convert electrical energy to other forms
• A circuit diagram – a simplified representation of an
actual circuit – is used to show the path of the real
circuit
• Circuit symbols are used to represent various elements
Resistors in Series
• When two or more resistors are connected end-to-end,
they are said to be in series
• The current is the same in all resistors because any
charge that flows through one resistor flows through
the other
• The sum of the potential differences across the
resistors is equal to the total potential difference
across the combination
I1  I 2  I
 V  IR1  IR 2  I ( R1  R2 )  IReq
Resistors in Series
 V  IReq
Req  R1  R2
• The equivalent resistance has the effect on the circuit
as the original combination of resistors (consequence
of conservation of energy)
• For more resistors in series:
Req  R1  R 2  R3  ...
• The equivalent resistance of a series combination of
resistors is greater than any of the individual resistors
emf and Internal Resistance
• A real battery has some internal resistance r;
therefore, the terminal voltage is not equal to the emf
• The terminal voltage: ΔV = Vb – Va
ΔV = ε – Ir
• For the entire circuit (R – load resistance):
ε = ΔV + Ir
= IR + Ir
emf and Internal Resistance
ε = ΔV + Ir = IR + Ir
• ε is equal to the terminal voltage when the current is
zero – open-circuit voltage
I = ε / (R + r)
• The current depends on both the resistance external to
the battery and the internal resistance
• When R >> r, r can be ignored
• Power relationship: I ε = I2 R + I2 r
• When R >> r, most of the power delivered by the
battery is transferred to the load resistor
Resistors in Parallel
I1 R1  I 2 R2   V
V V
I  I1  I 2 

R1
R2
• The potential difference across each resistor is the
same because each is connected directly across the
battery terminals
• The current, I, that enters a point must be equal to the
total current leaving that point (conservation of
charge)
• The currents are generally not the same
Resistors in Parallel
I1 R1  I 2 R2   V
V V
I  I1  I 2 

R1
R2
1
1  V
 V    
 R1 R2  Req
1
1
1
 
Req R1 R2
Resistors in Parallel
• For more resistors in parallel:
1
1
1
1
 
 
Req R1 R2 R3
• The inverse of the equivalent resistance of two or more
resistors connected in parallel is the algebraic sum of
the inverses of the individual resistance
• The equivalent is always less than the smallest
resistor in the group
Problem-Solving Strategy
• Combine all resistors in series
• They carry the same current
• The potential differences across them are not
necessarily the same
• The resistors add directly to give the equivalent
resistance of the combination:
Req = R1 + R2 + …
Problem-Solving Strategy
• Combine all resistors in parallel
• The potential differences across them are the same
• The currents through them are not necessarily the same
• The equivalent resistance of a parallel combination is
found through reciprocal addition:
1
1
1
 
 ...
Req R1 R2
Problem-Solving Strategy
• A complicated circuit consisting of several resistors
and batteries can often be reduced to a simple circuit
with only one resistor
• Replace resistors in series or in parallel with a single
resistor
• Sketch the new circuit after these changes have been
made
• Continue to replace any series or parallel combinations
• Continue until one equivalent resistance is found
Problem-Solving Strategy
• If the current in or the potential
difference across a resistor in
the complicated circuit is to be
identified, start with the final
circuit and gradually work back
through the circuits (use formula
ΔV = I R and the procedures
describe above)
Chapter 25
Problem 20
What resistance should you place in parallel with a 56-kΩ resistor to
make an equivalent resistance of 45 kΩ?
Kirchhoff’s Rules
• There are ways in which resistors can be connected
so that the circuits formed cannot be reduced to a
single equivalent resistor
• Two rules, called Kirchhoff’s Rules (Laws) can be
used instead:
• 1) Junction (Node) Rule
• 2) Loop Rule
Gustav Kirchhoff
1824 – 1887
Kirchhoff’s Rules
• Junction (Node) Rule (A statement of Conservation
of Charge): The sum of the currents entering any
junction must equal the sum of the currents leaving
that junction
• Loop Rule (A statement of Conservation of Energy):
The sum of the potential differences across all the
elements around any closed circuit loop must be
zero
Junction Rule
I1 = I2 + I3
• Assign symbols and directions to
the currents in all branches of the
circuit
• If a direction is chosen incorrectly,
the resulting answer will be
negative, but the magnitude will
be correct
Loop Rule
• When applying the loop rule, choose
a direction for transversing the loop
• Record voltage drops and rises as
they occur
• If a resistor is transversed in the
direction of the current, the potential
across the resistor is – IR
• If a resistor is transversed in the
direction opposite of the current, the
potential across the resistor is +IR
Loop Rule
• If a source of emf is transversed in
the direction of the emf (from – to +),
the change in the electric potential
is +ε
• If a source of emf is transversed in
the direction opposite of the emf
(from + to -), the change in the
electric potential is – ε
Equations from Kirchhoff’s Rules
• Use the junction rule as often as needed, so long as,
each time you write an equation, you include in it a
current that has not been used in a previous junction
rule equation
• The number of times the junction rule can be used is
one fewer than the number of junction points in the
circuit
• The loop rule can be used as often as needed so long
as a new circuit element (resistor or battery) or a new
current appears in each new equation
• You need as many independent equations as you have
unknowns
Equations from Kirchhoff’s Rules
Problem-Solving Strategy
• Draw the circuit diagram and assign labels and symbols
to all known and unknown quantities
• Assign directions to the currents
• Apply the junction rule to any junction in the circuit
• Apply the loop rule to as many loops as are needed to
solve for the unknowns
• Solve the equations simultaneously for the unknown
quantities
• Check your answers
Chapter 25
Problem 72
The figure shows a portion of a circuit used to model
muscle cells and neurons. All resistors have the same
value R = 1.5 MΩ, and the emfs are ε1 = 75 mV, ε2 = 45 mV
and ε3 = 20 mV. Find the current through ε3, including its
direction.
RC Circuits
• If a direct current circuit contains
capacitors and resistors, the
current will vary with time
• At the instant the switch is
closed, the charge on the
capacitor is zero
• When the circuit is completed,
the capacitor starts to charge,
and the potential difference
across the capacitor increases,
until the charge reaches its
maximum (Q = Cε)
Charging Capacitor in an RC Circuit
• Once the capacitor is fully charged (maximum
charge is reached), the current in the circuit is zero,
and the potential difference across the capacitor
matches that supplied by the battery
q
   IR  0
C

q

I
R RC
dq 
q
C  q
 

dt R RC
RC
Charging Capacitor in an RC Circuit
dq C  q

dt
RC
dq
dt

Q  q RC
dq
dt
 Q  q   RC
t
 ln q  Q  
 Const ' q  Q  e
RC t

q(t )  Q  e RC  Const
0

RC
q(0)  Q  e
 Q  Const  0
q(t )  Q(1  e

 Const
Const  Q
t
RC
)
t

RC
 Const
Charging Capacitor in an RC Circuit
• The charge on the capacitor
varies with time
q = Q (1 – e -t/RC )
• The time constant,  = RC,
represents the time required for
the charge to increase from zero
to 63.2% of its maximum
• In a circuit with a large (small) time constant, the
capacitor charges very slowly (quickly)
• After t = 10 , the capacitor is over 99.99% charged
Discharging Capacitor in an RC Circuit
• When a charged capacitor is
placed in the circuit, it can be
discharged
q
q dq
q
  IR  0 I  

C
RC dt
RC
t

dq
dt
RC


q
(
t
)

e
 Const
 q  RC
t

q (0)  Const  Q q(t )  Qe RC
d
I (t )  Qe
dt
t

RC
Q

e
RC
t

RC
Discharging Capacitor in an RC Circuit
• The charge on the capacitor varies
with time
q = Qe -t/RC
• The charge decreases
exponentially
• At t =  = RC, the charge
decreases to 0.368 Qmax; i.e., in
one time constant, the capacitor
loses 63.2% of its initial charge
Chapter 25
Problem 34
An uncharged 10-µF capacitor and a 470-kΩ resistor are in series, and
250 V is applied across the combination. How long does it take the
capacitor voltage to reach 200 V?
Meters in a Circuit – Ammeter, Voltmeter
• An ammeter is used to measure current in line with
the bulb – all the charge passing through the bulb
also must pass through the meter
• A voltmeter is used to measure voltage (potential
difference) – connects to the two ends of the bulb
Electrical Safety
• Electric shock can result in fatal burns
• Electric shock can cause the muscles of vital organs
(such as the heart) to malfunction
• The degree of damage depends on
– the magnitude of the current
– the length of time it acts
– the part of the body through which it passes
Effects of Various Currents
• 5 mA or less
– Can cause a sensation of shock
– Generally little or no damage
• 10 mA
– Hand muscles contract
– May be unable to let go a of live wire
• 100 mA
– If passes through the body for just a few seconds,
can be fatal
Answers to Even Numbered Problems
Chapter 25:
Problem 18
200 kJ
Answers to Even Numbered Problems
Chapter 25:
Problem 26
2A
Answers to Even Numbered Problems
Chapter 25:
Problem 30
1 kW
Answers to Even Numbered Problems
Chapter 25:
Problem 58
7.5 mJ