Download Answer

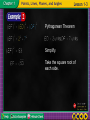
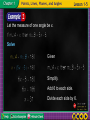
Glencoe Geometry Interactive Chalkboard
Copyright © by The McGraw-Hill Companies, Inc.
Developed by FSCreations, Inc., Cincinnati, Ohio 45202
Send all inquiries to:
GLENCOE DIVISION
Glencoe/McGraw-Hill
8787 Orion Place
Columbus, Ohio 43240
Lesson 1-1 Points, Lines, and Planes
Lesson 1-2 Linear Measure and Precision
Lesson 1-3 Distance and Midpoints
Lesson 1-4 Angle Measure
Lesson 1-5 Angle Relationships
Lesson 1-6 Polygons
Example 1 Name Lines and Planes
Example 2 Model Points, Lines, and Planes
Example 3 Draw Geometric Figures
Example 4 Interpret Drawings
Use the figure to name a line containing point K.
Answer: The line can be named as line a.
There are three points on the line. Any two of the points can
be used to name the line.
Use the figure to name a plane containing point L.
Answer: The plane can be named as plane B.
You can also use the letters of any three noncollinear
points to name the plane.
plane JKM
plane KLM
plane JLM
The letters of each of these names can be reordered to
create other acceptable names for this plane. For
example, JKM can also be written as JMK, MKJ, KJM,
KMJ, and MJK. There are 18 different three-letter names
for this plane.
Use the figure to name each of the following.
a. a line containing point X
Answer: line c,
b. a plane containing point Z
Answer: plane P, plane XYZ, plane ZYX, plane YZX,
plane XZY, plane ZXY, plane YXZ
VISUALIZATION Name the geometric shape
modeled by the long hand on a clock.
Answer: The long hand on a clock models a line segment.
VISUALIZATION Name the geometric shape
modeled by a 10  12 patio.
Answer: The patio models a plane.
VISUALIZATION Name the geometric shape
modeled by the location where the corner of a
driveway meets the road.
Answer: The location where the corner of a driveway
meets the road models a point.
VISUALIZATION Name the geometric shape
modeled by each object.
a. a colored dot on a map used to mark the location of a city
Answer: point
b. the ceiling of your classroom
Answer: plane
c. the railing on a stairway
Answer: line segment
Draw and label a figure for the following situation.
Plane R contains lines
and
, which intersect
at point P. Add point C on plane R so that it is not
collinear with
or
.
Draw a surface to represent plane R and label it.
Draw and label a figure for the following situation.
Plane R contains lines
and
, which intersect
at point P. Add point C on plane R so that it is not
collinear with
or
.
Draw a line anywhere on the plane.
Draw and label a figure for the following situation.
Plane R contains lines
and
, which intersect
at point P. Add point C on plane R so that it is not
collinear with
or
.
A
B
Draw dots on the line for points A and B. Label the points.
Draw and label a figure for the following situation.
Plane R contains lines
and
, which intersect
at point P. Add point C on plane R so that it is not
collinear with
or
.
A
B
Draw a line intersecting
.
Draw and label a figure for the following situation.
Plane R contains lines
and
, which intersect
at point P. Add point C on plane R so that it is not
collinear with
or
.
A
D
E
B
Draw dots on this line for points D and E. Label the points.
Draw and label a figure for the following situation.
Plane R contains lines
and
, which intersect
at point P. Add point C on plane R so that it is not
collinear with
or
.
A
E
D P
B
Label the intersection point of the two lines as P.
Draw and label a figure for the following situation.
Plane R contains lines
and
, which intersect
at point P. Add point C on plane R so that it is not
collinear with
or
.
Answer:
A
C
E
D P
B
Draw a dot for point C in plane R such that it will not lie
on
or
. Label the point.
Draw and label a figure for the following situation.
on a coordinate plane contains Q(–2, 4) and
R(4, –4). Add point T so that T is collinear with these
points.
Graph each point and draw
There are an infinite number
of points that are collinear
with Q and R. In the graph,
one such point is T(1, 0).
.
Draw and label a figure for each relationship.
a. Plane D contains line a, line m, and line t, with all
three lines intersecting at point Z. Add point F on
plane D so that it is not collinear with any of the three
given lines.
Sample answer:
Draw and label a figure for each relationship.
b.
on a coordinate plane contains B(–3, –2) and A(3, 2).
Add point M so that M is collinear with these points.
Sample answer:
How many planes appear in this figure?
Answer: There are two planes: plane S and plane ABC.
Name three points that are collinear.
Answer: Points A, B, and D are collinear.
Are points A, B, C, and D coplanar? Explain.
Answer: Points A, B, C, and D all lie in
plane ABC, so they are coplanar.
At what point do
and
intersect?
Answer: The two lines intersect at point A.
a. How many planes appear in this figure?
Answer: two
b. Name three points that are collinear.
Sample answer: A, X, and Z
c. Are points X, O, and R coplanar? Explain.
Answer: Points X, O, and R all lie in
plane T, so they are coplanar.
d. At what point do
Answer: R
and
intersect?
Example 1 Length in Metric Units
Example 2 Length in Customary Units
Example 3 Precision
Example 4 Find Measurements
Example 5 Congruent Segments
Find the length of
.
The long marks are centimeters, and the shorter marks are
millimeters. There are 10 millimeters for each centimeter.
Answer:
is about 42 millimeters long.
Find the length of
.
The ruler is marked in centimeters. Point R is closer to the
5-centimeter mark than to 4 centimeters.
Answer:
is about 5 centimeters long.
a. Find the length of
Answer: 18 mm
b. Find the length of
Answer: 2 cm
Find the length of
.
Each inch is divided into sixteenths. Point E is closer
to the 3-inch mark.
Answer:
is about 3 inches long.
Find the length of
.
Each inch is divided into fourths. Point G is closer to the
-inch mark.
Answer:
is about
inches long.
a. Find the length of
Answer:
in.
.
b. Find the length of
Answer:
in.
.
Find the precision for
inches. Explain its meaning.
The measuring tool is divided into
-inch increments. Thus,
the measurement is precise to within
Answer: The precision is
be
inches to
inch.
inch. The measurement could
inches.
Find the precision for 15 millimeters. Explain its
meaning.
The measuring tool is divided into millimeter increments.
Thus, the measurement is precise to within
(1) or
0.5 millimeter.
Answer: The precision is 0.5 millimeter. The
measurement could be 14.5 millimeters
to 15.5 millimeters.
PRECISION Find the precision for each measurement.
Explain its meaning.
a. 88 millimeters
Answer: The precision is 0.5 millimeter. The measurement
could be 87.5 millimeters to 88.5 millimeters.
b.
Answer: The precision is
could be
inch. The measurement
inches to
inches.
Find LM.
LM is the measure of
.
Point M is between L and N.
Sum of parts
whole
Substitution
Subtract 2.6 from each side.
Simplify.
Answer:
is 1.4 centimeters long.
Find XZ.
XZ is the measure of
.
Point Y is between X and Z. XZ can be found by adding
XY and YZ.
Sum of parts
Substitution
Add.
whole
Answer:
is
inches long.
Find x and ST if T is between S and U, ST
and TU 5x – 3.
7x, SU
Substitute known values.
Add 3 to each side.
Simplify.
Divide each side by 12.
Simplify.
45,
Given
Multiply.
Answer:
a. Find SE.
Answer:
in.
b. Find ON.
Answer: 3.7 cm
c. Find a and AB if AB 4a + 10, BC
Answer:
3a – 5, and AC 19.
FONTS The Arial font is often used because it is easy
to read. Study the word time shown in Arial type.
Each letter can be broken into individual segments.
The letter T would have two segments, a short
horizontal segment, and a long vertical segment.
Assume that all segments overlap when they meet.
Which segments are congruent?
TIME
Answer: The five vertical segments in the letters T, I, M,
and E are congruent. The four horizontal segments in T
and E are congruent. The two diagonal segments in the
letter M are congruent.
LEISURE ACTIVITIES
The graph shows
the percent of
adults who
participated in
selected activities.
Suppose a
segment was
drawn along the
height of each bar.
Which categories
would have
segments that
are congruent?
Answer: The segments on the bars for going to museums
and picnics would be congruent because they
both have the same height, representing 16%.
The segments on bars for going to the zoo and
playing board games would be congruent
because they have the same height,
representing 14%.
Example 1 Find Distance on a Number Line
Example 2 Find Distance on a Coordinate Plane
Example 3 Find Coordinates of Midpoint
Example 4 Find Coordinates of Endpoint
Example 5 Use Algebra to Find Measures
Use the number line to find QR.
The coordinates of Q and R are –6 and –3.
Distance Formula
Simplify.
Answer: 3
Use the number line to find AX.
Answer: 8
Find the distance between E(–4, 1) and F(3, –1).
Method 1 Pythagorean Theorem
Use the gridlines to form
a triangle so you can use
the Pythagorean
Theorem.
Pythagorean Theorem
Simplify.
Take the square root of
each side.
Method 2 Distance Formula
Distance Formula
Simplify.
Simplify.
Answer: The distance from E to F is
units.
You can use a calculator to find that
is approximately 7.28.
Find the distance between A(–3, 4) and M(1, 2).
Answer:
The coordinates on a number line of J and K are –12
and 16, respectively. Find the coordinate of the
midpoint of
.
The coordinates of J and K are –12 and 16.
Let M be the midpoint of
.
Simplify.
Answer: 2
Find the coordinates of M, the midpoint of
for G(8, –6) and H(–14, 12).
Let G be
Answer: (–3, 3)
and H be
.
,
a. The coordinates on a number line of Y and O are
7 and –15, respectively. Find the coordinate of the
midpoint of
.
Answer: –4
b. Find the coordinates of the midpoint of
for X(–2, 3) and Y(–8, –9).
Answer: (–5, –3)
Find the coordinates of D if E(–6, 4) is the midpoint
of
and F has coordinates (–5, –3).
Let F be
in the Midpoint Formula.
Write two equations to find the coordinates of D.
Solve each equation.
Multiply each side by 2.
Add 5 to each side.
Multiply each side by 2.
Add 3 to each side.
Answer: The coordinates of D are (–7, 11).
Find the coordinates of R if N(8, –3) is the midpoint
of
and S has coordinates (–1, 5).
Answer: (17, –11)
Multiple-Choice Test Item
What is the measure of
if Q is the midpoint of
A
B4
C
D9
?
Read the Test Item
You know that Q is the midpoint of
, and the figure gives
algebraic measures for
and
. You are asked to find
the measure of
.
Solve the Test Item
Because Q is the midpoint, you know that
.
Use this equation and the algebraic measures to find a
value for x.
Definition of midpoint
Distributive Property
Subtract 1 from each side.
Add 3x to each side.
Divide each side by 10.
Now substitute
for x in the expression for PR.
Original measure
Simplify.
Answer: D
Multiple-Choice Test Item
What is the measure of
if B is the midpoint of
A1
Answer: B
B3
C5
D 10
?
Example 1 Angles and Their Parts
Example 2 Measure and Classify Angles
Example 3 Use Algebra to Find Angle Measures
Name all angles that have B as a vertex.
Answer: 5, 6, 7, and ABG
Name the sides of 5.
Answer:
and
or
are the sides of 5.
Write another name for 6.
Answer: EBD, FBD, DBF, and DBE
are other names for 6.
a. Name all angles that have X as a vertex.
Answer: 1, 2, 3, and RXB
or RXN
b. Name the sides of 3.
Answer:
c. Write another name for 3.
Answer: AXB, AXN, NXA, BXA
Measure TYV and classify it as
right, acute, or obtuse.
TYV is marked with
a right angle symbol,
so measuring is not
necessary.
Answer:
is a right angle.
Measure WYT and classify it as
right, acute, or obtuse.
Use a protractor to find
that
.
Answer:
>
is an obtuse angle.
Measure TYU and classify it as
right, acute, or obtuse.
Use a protractor to find
that m
.
Answer:
is an acute angle.
Measure each angle named and classify
it as right, acute, or obtuse.
a. CZD
Answer: 150, obtuse
b. CZE
Answer: 90, right
c. DZX
Answer: 30, acute
INTERIOR DESIGN Wall stickers of standard shapes
are often used to provide a stimulating environment
for a young child’s room. A five-pointed star sticker
is shown with vertices labeled. Find mGBH and
mHCI if GBH HCI, mGBH 2x + 5, and
mHCI 3x – 10.
Given
Definition of congruent angles
Substitution
Add 10 to each side.
Subtract 2x from each side.
Use the value of x to find the measure of one angle.
Given
or 35
Since
Answer: Both
Simplify.
.
measure 35.
SIGNS A railroad crossing sign forms congruent
angles. In the figure, WVX ZVY. If mWVX 7a + 13
and mZVY 10a – 20, find the actual measurements of
WVX and ZVY.
Answer:
Example 1 Identify Angle Pairs
Example 2 Angle Measure
Example 3 Perpendicular Lines
Example 4 Interpret Figures
Name two angles that form a linear pair.
A linear pair is a pair of
adjacent angles whose
noncommon sides are
opposite rays.
Answer: The angle pairs that satisfy this definition are
Name two acute vertical angles.
There are four acute
angles shown. There is one
pair of vertical angles.
Answer: The acute vertical angles are VZY
and XZW.
Name an angle pair that satisfies each condition.
a. two acute vertical angles
Answer: BAC and FAE,
CAD and NAF, or
BAD and NAE
b. two adjacent angles whose
sum is less than 90
Answer: BAC and CAD or
EAF and FAN
ALGEBRA Find the measures of two supplementary
angles if the measure of one angle is 6 less than five
times the other angle.
Explore
The problem relates the measures of two
supplementary angles. You know that the sum
of the measures of supplementary angles is 180.
Plan
Draw two figures to represent the angles.
Let the measure of one angle be x.
Solve
Given
Simplify.
Add 6 to each side.
Divide each side by 6.
Use the value of x to find each angle measure.
Examine Add the angle measures to verify that the
angles are supplementary.
Answer: 31, 149
ALGEBRA Find the measures of two complementary
angles if one angle measures six degrees less than
five times the measure of the other.
Answer: 16, 74
ALGEBRA Find x so that
.
If
IJH.
, then mKJH
90. To find x, use KJI and
Sum of parts
whole
Substitution
Add.
Subtract 6 from each side.
Divide each side by 12.
Answer:
ALGEBRA Find x and y so that
are perpendicular.
Answer:
and
Determine whether the following statement can be
assumed from the figure below. Explain.
mVYT
90
The diagram is marked to
show that
From the definition of
perpendicular, perpendicular
lines intersect to form
congruent adjacent angles.
Answer: Yes;
and
are perpendicular.
Determine whether the following statement can be
assumed from the figure below. Explain.
TYW and TYU are supplementary.
Answer: Yes; they form a
linear pair of angles.
Determine whether the following statement can be
assumed from the figure below. Explain.
VYW and TYS are adjacent angles.
Answer: No; they do not
share a common side.
Determine whether each statement can be assumed
from the figure below. Explain.
a.
Answer: Yes; lines TY and SX
are perpendicular.
b. TAU and UAY are
complementary.
Answer: No; the sum of the
two angles is 180, not 90.
c. UAX and UXA are adjacent.
Answer: No; they do not share
a common side.
Example 1 Identify Polygons
Example 2 Find Perimeter
Example 3 Perimeter on the Coordinate Plane
Example 4 Use Perimeter to Find Sides
Name the polygon by its number of sides. Then
classify it as convex or concave, regular or irregular.
There are 4 sides, so this is a quadrilateral.
No line containing any of the sides will pass through the
interior of the quadrilateral, so it is convex.
The sides are not congruent, so it is irregular.
Answer: quadrilateral, convex, irregular
Name the polygon by its number of sides. Then
classify it as convex or concave, regular or irregular.
There are 9 sides, so this is a nonagon.
A line containing some of the sides will pass through the
interior of the nonagon, so it is concave.
The sides are not congruent, so it is irregular.
Answer: nonagon, concave, irregular
Name each polygon by the number of sides. Then
classify it as convex or concave, regular or irregular.
a.
Answer: triangle, convex, regular
b.
Answer: quadrilateral, convex, irregular
CONSTRUCTION
A masonry company is contracted to lay three
layers of decorative brick along the foundation for a
new house given the dimensions below. Find the
perimeter of the foundation and determine how
many bricks the company will need to complete the
job. Assume that one brick is 8 inches long.
First, find the perimeter.
Add the lengths
of the sides.
The perimeter of the foundation is 216 feet.
Next, determine how many bricks will be needed to
complete the job. Each brick measures 8 inches, or
Divide 216 by
foot.
to find the number of bricks needed for
one layer.
Answer: The builder will need 324 bricks for each layer.
Three layers of bricks are needed, so the
builder needs 324 • 3 or 972 bricks.
CONSTRUCTION
The builder realizes he accidentally halved the size of
the foundation in part a. How will this affect the
perimeter of the house and the number of bricks the
masonry company needs?
The new dimensions are twice the measures of the
original lengths.
The perimeter has doubled.
The new number of bricks needed for one layer is
or 648. For three layers, the total number of
bricks is 648 • 3 or 1944 bricks.
Answer: The perimeter and the number of bricks
needed are doubled.
SEWING Miranda is making a very unusual quilt. It is in
the shape of a hexagon as shown below. She wants to
trim the edge with a special blanket binding.
The binding is sold by the yard.
a. Find the perimeter of the
quilt in inches. Then
determine how many yards
of binding Miranda
will need for the quilt.
Answer: 336 in.,
yd
SEWING Miranda is making a very unusual quilt. It is in
the shape of a hexagon as shown below. She wants to
trim the edge with a special blanket binding.
The binding is sold by the yard.
b. Miranda decides to make
four quilts. How will this
affect the amount of
binding she will need? How
much binding will she need
for this project?
Answer: The amount of binding is multiplied by 4.
She will need
yards.
Find the perimeter of pentagon ABCDE with A(0, 4),
B(4, 0), C(3, –4), D(–3, –4), and E(–3, 1).
Use the Distance Formula,
to find AB, BC, CD, DE, and EA.
,
Answer: The perimeter of pentagon ABCDE is
or about 25 units.
Find the perimeter of quadrilateral WXYZ with
W(2, 4), X(–3, 3), Y(–1, 0), and Z(3, –1).
Answer: about 17.9 units
The width of a rectangle is 5 less than twice its length.
The perimeter is 80 centimeters. Find the length of each
side.
Let
represent the length. Then the width is
.
Perimeter formula for rectangle
Multiply.
Simplify.
Add 10 to each side.
Divide each side by 6.
The length is 15 cm. By substituting 15 for ,
the width becomes 2(15) – 5 or 25 cm.
Answer:
The length of a rectangle is 7 more than five times its
width. The perimeter is 134 feet. Find the length of
each side.
Answer:
Explore online information about the
information introduced in this chapter.
Click on the Connect button to launch your browser
and go to the Glencoe Geometry Web site. At this site,
you will find extra examples for each lesson in the
Student Edition of your textbook. When you finish
exploring, exit the browser program to return to this
presentation. If you experience difficulty connecting to
the Web site, manually launch your Web browser and
go to www.geometryonline.com/extra_examples.
Click the mouse button or press the
Space Bar to display the answers.
Click the mouse button or press the
Space Bar to display the answers.
Click the mouse button or press the
Space Bar to display the answers.
Click the mouse button or press the
Space Bar to display the answers.
Click the mouse button or press the
Space Bar to display the answers.
Click the mouse button or press the
Space Bar to display the answers.
End of Custom Shows
WARNING! Do Not Remove
This slide is intentionally blank and is set to auto-advance to end
custom shows and return to the main presentation.