Download E - York University

Electrochemistry
Reading: from Petrucci, Harwood and Herring (8th edition):
Required for Part 1: Sections 21-1 through 21-4.
Examples for Part 1: 21-1 through 21-10.
Problem Set for Part 1:
Review: Chapter 5 questions 21-26.
Chapter 21 questions: 15-17, 32, 34, 43, 53
Additional problems from Chapter 21:
York University CHEM 1001 3.0
Electrochemistry - 1
Applications of Electrochemistry
C Spontaneous chemical reactions can be used to produce
an electric current and do work. (batteries, fuel-cells)
C An electric current can be used to force non-spontaneous
chemical reactions to occur. (electrolysis)
C Reactions can be made to occur in a specific place.
(electroplating, electropolishing)
C The voltage produced by a reaction can be used as an
analytical tool. (pH electrodes)
C The current produced by a reaction can be used as an
analytical tool.
York University CHEM 1001 3.0
Electrochemistry - 2
)G and non-PV Work
For a reversible process at constant T and P:
)H = qP + wE
(definition of enthalpy)
wE = non-PV work done on the system
qP = T)S
(reversible, constant T)
Let wmax = maximum non-PV work done by the system
wmax = -wE
So
(reversible)
wmax = -)H + T)S = -)G
Conclusion: The maximum non-PV work that can be
obtained from a process is equal to -)G.
York University CHEM 1001 3.0
Electrochemistry - 3
Work from Chemical Reactions
Spontaneous chemical reactions can be used to do work.
How?
One possibility:
C burn fuel to release heat
C boil water
C use the expanding steam to do work
Disadvantages:
C inefficient (only part of heat can be turned into work)
C can not readily carry out the reverse process
York University CHEM 1001 3.0
Electrochemistry - 4
Work from Redox Reactions
Another method: Use redox reactions.
Cu(s) + 2Ag+ W Cu2+ + 2Ag(s)
)rG° = -88.43 kJ mol-1
The Cu(s) is oxidized (gives up electrons).
Half-reaction: Cu(s) 6 Cu2+ + 2eThe Ag+(aq) is reduced (receives electrons).
Half-reaction: Ag+ + e- 6 2Ag(s)
This reaction is spontaneous. If we can transfer the electrons
through an external circuit, we can use it do electrical work.
York University CHEM 1001 3.0
Electrochemistry - 5
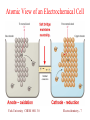
Electrochemical Cells
C Cu is oxidized at
one electrode:
Cu(s) 6 Cu2+ + 2eC Ag+ is reduced at
the other electrode:
e- + Ag+ 6 Ag(s)
C Electrons travel
through the wire.
C Ions travel through
the salt bridge.
York University CHEM 1001 3.0
Electrochemistry - 6
Atomic View of an Electrochemical Cell
York University CHEM 1001 3.0
Electrochemistry - 7
Electrochemical Cells - Terminology
C The anode is the electrode at which oxidation occurs.
C The cathode is the electrode at which reduction occurs.
C The cell potential is the voltage difference when no
current flows between the electrodes.
Cell potential is also called cell voltage or EMF
(electromotive force).
C Cells in which spontaneous reactions produce a current
are called voltaic cells or galvanic cells.
C In electrolytic cells electricity is used to force a nonspontaneous reaction to occur.
York University CHEM 1001 3.0
Electrochemistry - 8
Cell Diagrams
C Anode (oxidation) is placed on left side of diagram.
C Cathode (reduction) is placed on right side of diagram.
C Single vertical line, | , indicates a boundary between
different phases (i.e., solution | solid).
C Double vertical line, || , indicates a boundary (salt bridge)
between different half-cell compartments.
Example:
Cu(s) * Cu2+ 2 Ag+ * Ag(s)
At the anode:
Cu(s) 6 Cu2+ + 2e-
At the cathode:
Ag+ + e- 6 Ag(s)
Overall:
Cu(s) + 2Ag+ 6 Cu2+ + 2Ag(s)
York University CHEM 1001 3.0
Electrochemistry - 9
Cell Diagrams - examples
Diagram the cell in which the following overall reaction
occurs:
Pb(s) + 2AgCl(s) W PbCl2(s) + 2Ag(s)
Answer: Pb(s)*Cl-(aq)*PbCl2(s))2AgCl(s)*Ag(s)*Cl-(aq)*
Write the half-cell reactions for the following cell:
Ag(s)*Ag+(aq)2Cl-(aq)*AgCl(s)*Ag(s)
Answer:
Anode (oxidation):
Ag(s) 6 Ag+(aq) + eCathode (reduction): AgCl(s) + e- 6 Ag(s) + Cl-(aq)
York University CHEM 1001 3.0
Electrochemistry - 10
Balancing Redox Reactions - Review
Example:
SO32- + MnO 4- W SO42- + Mn2+
(unbalanced)
S from +4 to +6 (oxidized). Mn from +7 to +2 (reduced).
(1) Write balanced half-reactions for oxidation and
reduction.
Oxidation half-reaction
Skeleton reaction: SO32- W SO42- + 2eBalanced:
SO32- + H2O(l) W SO42- + 2H+ + 2eReduction half-reaction
Skeleton reaction: MnO 4- + 5e- W Mn2+
Balanced:
MnO 4- + 8H+ + 5e- W Mn2+ + 4H2O(l)
York University CHEM 1001 3.0
Electrochemistry - 11
Balancing Redox Reactions - continued
(2) Adjust coefficients so the two half-reactions have the
same numbers of electrons.
5SO32- + 5H2O(l) W 5SO42- + 10H+ + 10e2MnO 4- + 16H+ + 10e- W 2Mn2+ + 8H2O(l)
(3) Add the two half-reactions.
5SO32- + 2MnO 4- + 6H+ W 5SO42- + 2Mn2+ + 3H2O(l)
10 electrons are transferred (important for later).
(4) Check that the reaction is balanced for both atoms and
charge.
York University CHEM 1001 3.0
Electrochemistry - 12
Redox Reactions in Basic Solution
5SO32- + 2MnO 4- + 6H+ W 5SO42- + 2Mn2+ + 3H2O(l)
Since this balanced reaction involves H +, it is appropriate
for acidic solution
For the reaction in basic solution, add
6 × {H2O(l) W H+ + OH-}
This gives:
5SO32- + 2MnO 4- + 3H2O(l) W 5SO42- + 2Mn2+ + 6OHThis method can also be used to get half-reactions in basic
solution.
York University CHEM 1001 3.0
Electrochemistry - 13
Current and Charge
C Current is the amount of charge transferred per unit time.
C The amount of charge transferred is determined by the
stoichiometry of the cell reaction.
C The charge on one mole of electrons is 96,485 coulombs.
This is called the Faraday constant, F.
F = 96,485 C mol-1 = 96,485 J V -1 mol-1
Example:
Cu(s) + 2Ag+ 6 Cu2+ + 2Ag(s)
1.93×105 C are transferred per mole of Cu oxidized.
C The current produced by a cell is determined by the reaction
kinetics and the resistance of the circuit.
York University CHEM 1001 3.0
Electrochemistry - 14
Electrical Work
The work done in an electrical circuit is
welec = charge × (potential difference)
Units:
coulombs × volts = joules
The maximum possible non-PV work equals -)G. Let
n / moles of electrons transferred per mole of reaction
nF = total charge (coulombs) transferred
Ecell / maximum possible cell potential (requires zero
current)
Then:
)rG = -nFEcell
York University CHEM 1001 3.0
Electrochemistry - 15
Electrical Work - continued
)rG = -nFEcell
There is a fundamental connection between )rG and cell
potential. Because of this:
C Cell potentials depend on concentrations.
C Electrochemical cells can be used to measure
concentrations. (pH electrodes, for example)
C Electrochemical cells can be used to measure )rG (and
to determine )rG°).
C Tabulated thermodynamic data can be used to determine
cell potentials.
York University CHEM 1001 3.0
Electrochemistry - 16
Cell Potential - Example
A cell is constructed in which the half-cell reactions are:
Anode:
H2(g) 6 2H+(aq) + 2e-
Cathode:
Cl2(g) + 2e- 6 2Cl-(aq)
When PH2 = PCl2 = 1.000 atm and [H +] = [Cl-] = 0.0100 M,
the cell potential is found to be 1.4813 volts. Find )rG
under these conditions for
H2(g) + Cl2(g) W 2H+(aq) + 2Cl-(aq)
Solution: )rG = -nFEcell and n = 2 for the overall reaction.
)rG = -2(96,485 J V -1 mol-1)(1.4813 V) = -285.85 kJ mol-1
York University CHEM 1001 3.0
Electrochemistry - 17
Cell Potentials and Spontaneity
)rG = -nFEcell
C If )rG < 0, the reaction is spontaneous as written.
C If )rG > 0, the reaction is non-spontaneous as written
(reverse reaction is spontaneous).
If the reaction proceeds as written, then n > 0.
Therefore:
C If Ecell > 0, the reaction is spontaneous as written.
C If Ecell < 0, the reaction is non-spontaneous as written.
York University CHEM 1001 3.0
Electrochemistry - 18
Standard Cell Potentials
C Definition: The standard cell potential, E°cell, is the cell
potential that would obtain if all reactants and products were
in their standard states.
C Therefore:
)rG° = -nFE°cell
C Standard states may be hypothetical. The standard cell
potential is used in calculations of actual cell potentials.
C The standard cell potential is the sum of standard potentials
for the individual half-cells.
York University CHEM 1001 3.0
Electrochemistry - 19
Standard Cell Potential - example
The cell with the overall reaction
H2(g) + Cl2(g) W 2H+(aq) + 2Cl-(aq)
has a standard cell potential of 1.3604 V. Determine )fG°
for Cl-(aq).
Solution:
)rG° = -nFE°cell
)rG° = -2(96,485 C mol-1)(1.3604 V) = -262.52 kJ mol-1
For H 2(g), Cl2(g), and H+(aq); )fG° = 0.
Y )rG° = 2)fG°(Cl-(aq))
Y )fG°(Cl-(aq)) = -131.26 kJ mol-1
York University CHEM 1001 3.0
Electrochemistry - 20
Standard Hydrogen Electrode
C To create a voltage, we need two half-cells. So we
can't measure individual half-cell potentials.
C Convention: The standard hydrogen electrode is
assigned a half-cell potential of zero.
2H+(aq) + 2e- 6 H2(g)
E° = 0 volts
Standard states (a=1): [H+] . 1 M, PH2 = 1 bar . 1 atm
C The half-cell potential will differ from zero if H+ and/or
H2 are not in their standard states.
York University CHEM 1001 3.0
Electrochemistry - 21
Standard Hydrogen Electrode - continued
C H2(g) at one bar
bubbled over a
platinum electrode.
C Pt acts a catalyst for
the reaction.
C 2H+ + 2e- 6 H2(g)
C Used as a basis for
calculations. Not
really very practical.
York University CHEM 1001 3.0
Electrochemistry - 22
Standard Electrode Potentials
The standard electrode potential for a half-cell is the
potential when all species are in their standard states.
C refers to reduction at the electrode (these days)
C measured relative to a standard hydrogen electrode as
the anode
Example: Cell for measuring E° for Cu2+/Cu.
Anode:
H2(g) 6 2H+ + 2e-
(oxidation)
Cathode:
Cu2+(1 M) + 2e- 6 Cu(s)
(reduction)
Cell Diagram: Pt*H2(1 bar)*H+(1 M)2Cu2+(1 M)*Cu(s)
Cell potential is 0.340 V. So E° = 0.340 V for Cu2+/Cu.
York University CHEM 1001 3.0
Electrochemistry - 23
Standard Electrode Potentials - continued
Reduction Half-Reaction
F2(g) + 2e- 6 2F-(aq)
E° (volts)
2.866
O2(g) + 4H+(aq) + 4e- 6 2H2O(l) 1.229
2H+(aq) + 2e- 6 H2(g)
0.000
Zn2+(aq) + 2e- 6 Zn(s)
-0.763
Li+(aq) + e- 6 Li(s)
-3.040
F2 is easiest to reduce (largest E°). F- is hardest to oxidize.
Li+ is hardest to reduce. Li is easiest to oxidize.
F2 is best oxidizing agent; Li is best reducing agent.
York University CHEM 1001 3.0
Electrochemistry - 24
Using Standard Electrode Potentials
A standard cell potential, E°cell, may be calculated from the
standard electrode potentials for the cathode, E°cathode, and
anode, E°anode:
E°cell = E°cathode - E°anode
C The anode potential is subtracted since the potential is for
reduction and the anode reaction is oxidation.
C Standard electrode potentials are listed in tables.
C Standard electrode potentials do not depend on how a
reaction is written since they are related to )rG° per mole
of electrons. ()rG° = -nFE°cell)
York University CHEM 1001 3.0
Electrochemistry - 25
Standard Electrode Potentials - example
Find the standard cell potential for the reaction:
Zn(s) + Cl2(g) W Zn2+(aq) + 2Cl-(aq)
Solution: Write half-cell reactions and find E° values.
Oxidation: Zn(s) 6 Zn2+(aq) + 2eReduction: Cl2(g) + 2e- 6 2Cl-(aq)
From Table 21.1:
Zn2+(aq) + 2e- 6 Zn(s)
E° = -0.763 V
Cl2(g) + 2e- 6 2Cl-(aq)
E° = 1.358 V
E°cell = E°cathode - E°anode = 1.358 - (-0.763) = 2.121 V
York University CHEM 1001 3.0
Electrochemistry - 26
Cell Potential and Equilibrium Constant
We have derived the following two equations:
)rG° = -nFE°cell
and
)rG° = -RTln Keq
Combining these gives
E°cell =
lnKeq
Uses of this equation:
C Calculating Keq from standard half-cell potentials (see
example 21-7 in text).
C Relating E°cell for different reactions.
York University CHEM 1001 3.0
Electrochemistry - 27
Cell Potential and Equilibrium - Example
At 298.15 K, the standard reduction potential for O2(g) in
acidic solution is 1.229 V:
O2(g) + 4H+(aq) + 4e- 6 2H2O(l)
E1° = 1.229 V
Find the standard reduction potential for O2(g) in basic
solution:
O2(g) + 2H2O(l) + 4e- 6 4OH-(aq)
E 2° = ?
Solution: The second reaction is equal to the first plus
4H2O(l) W 4H+(aq) + 4OH-(aq)
Keq = KW4
So K2 = K1KW4, E2° = (RT/nF)ln(K1KW4), n = 4
Y E2° = E1° + (RT/F)lnKW = 1.229 + 0.02569 ln(1.0×10-14)
E2° = 0.401 V
York University CHEM 1001 3.0
Electrochemistry - 28
Dissolving Metals with Acids
Many metals are dissolved by acids with the evolution
of H2(g).
Oxidation: M(s) 6 Mn+(aq) + ne-
E° = E°M
Reduction: 2H+(aq) + 2e- 6 H2(g)
E° = 0
Overall: M(s) + nH+(aq) 6 Mn+(aq) + (n/2)H2(g) E° = -E°M
Conclusions:
C The more negative the standard reduction potential of the
metal ion, the easier the metal is to dissolve.
C Lowering the pH promotes the dissolution of metals.
York University CHEM 1001 3.0
Electrochemistry - 29
Dissolving Metals with Acids - example
Determine the concentrations of each of the following
metals that will dissolve at pH = 7.00 and pH = 0.00.
Cu2+(aq) + 2e- 6 Cu(s)
E° = 0.340 V
Pb2+(aq) + 2e- 6 Pb(s)
E° = -0.125 V
Zn2+(aq) + 2e- 6 Zn(s)
E° = -0.763 V
Solution: M(s) + 2H+(aq) 6 M2+(aq) + H2(g)
n=2
E°cell = -E°
T = 298.15 K
PH2 . 1 bar
E°cell = (RT/nF)lnKeq Y Keq = exp(-(77.85 V-1)E°)
Y [M2+] . [H+]2 Keq = [H+]2 exp(-(77.85 V-1)E°)
York University CHEM 1001 3.0
Electrochemistry - 30
Dissolving Metals with Acids - continued
[M2+] . [H+]2 exp(-(77.85 V-1)E°)
pH = 7
E° (V)
pH = 0
[Cu2+]eq = 3.2×10-26 M
3.2×10-12 M
0.340
[Pb2+]eq = 1.7×10-10 M
1.7×104 M
-0.125
[Zn2+]eq = 6.3×1011 M
6.3×1025 M
-0.763
C Metals with E° o 0 are difficult to dissolve even in
strong acids.
C Metals with E° - 0 will dissolve in strong acids.
C Metals with E° n 0 will dissolve in water.
York University CHEM 1001 3.0
Electrochemistry - 31
Enhancing Dissolution of Metals
C Concentrated HNO3 will dissolve Cu(s):
Cu2+(aq) + 2e- 6 Cu(s)
NO3- + 4H+ + 4e- 6 NO(g) + H2O(l)
E° = 0.340 V
E° = 0.956 V
For the overall reaction, E° = (0.956 - 0.340) V = 0.616 V.
This is very favorable.
C Gold can be dissolved using aqua regia (1 part HNO3 to
3 parts HCl):
Au3+(aq) + 3e- 6 Au(s)
E° = 1.52 V
Au3+(aq) + 4Cl-(aq) W [AuCl4]-(aq)
York University CHEM 1001 3.0
Electrochemistry - 32
The Nernst Equation
We have shown that
)rG = -nFEcell
But )rG depends on the concentrations of reactants and
products:
)rG = )rG° + RTlnQ
Therefore, Ecell also depends on concentrations. Combining
these gives nFEcell = nFE°cell - RTlnQ. So
This is known as the Nernst Equation.
York University CHEM 1001 3.0
Electrochemistry - 33
The Nernst Equation - continued
Here:
R = 8.314 J mol-1 K-1
F = 96,485 C mol-1 = 96,485 J V -1 mol-1
lnQ = ln(10)×logQ = 2.303 logQ
So
Ecell = E°cell - (1.984×10-4 V K-1)(T/n)logQ
If T = 298.15 K (25 °C), then
Ecell = E°cell - (1/n)(0.05916 V)logQ
York University CHEM 1001 3.0
Electrochemistry - 34
Using the Nernst Equation
Find Ecell at 298 K for the cell
Pt*Fe2+(0.10 M),Fe3+(0.20 M)2Ag+(1.0 M)*Ag(s)
Solution: First find E°cell, then use the Nernst Equation.
Anode:
Fe2+ 6 Fe3+ + e-
E° = 0.771 V
Cathode:
Ag+ + e- 6 Ag(s)
E° = 0.800 V
Cell:
Fe2+ + Ag+ 6 Fe3+ + Ag(s)
E°cell = E°cathode - E°anode = 0.029 V
n=1
Q = [Fe3+] / [Fe2+][Ag+] = (0.20) / (0.10)(1.0) = 2.0
Ecell = E°cell - (1/n)(0.05916 V)logQ = 0.011 V
York University CHEM 1001 3.0
Electrochemistry - 35
Concentration Cells
We can make a cell
with the same
reaction occuring at
both electrodes.
Y E°cell = 0
The cell voltage is
due to the difference
in concentration.
York University CHEM 1001 3.0
Electrochemistry - 36
Determining Ksp
With saturated AgI(aq) at the anode and [Ag+] = 0.100 M at
the cathode, Ecell = 0.417 V. Use this to find Ksp.
Anode:
Ag(s) 6 Ag+(aq, sat. AgI) + e-
Cathode:
Ag+(aq, 0.1M) + e- 6 Ag(s)
Cell:
Ag+(aq, 0.1M) 6 Ag+(aq, sat. AgI)
E°cell = 0. Q = [Ag+]sat,KI / [0.1 M]. n = 1.
The Nernst equation becomes (at 298.15 K):
0.417 V = Ecell = - (0.05916 V) log([Ag+]sat,KI / [0.1 M])
Y [Ag+]sat,KI = [0.1 M] 10-7.049 = 8.94×10-9 M
Y Ksp = [I-][Ag+] = (8.94×10-9)2 = 7.99×10-17
York University CHEM 1001 3.0
Electrochemistry - 37
Electrochemistry Basics - Summary
C Electrochemical cells permit us to couple electrical
work to chemical reactions.
C Cell potential and )rG are directly related:
)rG = -nFEcell.
C Standard reduction potentials are tabulated and may
be used to compute E°cell and )rG°.
C The effect of concentration on cell potential is given
by the Nernst equation:
York University CHEM 1001 3.0
Electrochemistry - 38