Download Discrete Mathematics Project part II

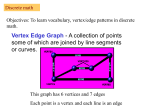
Angie
Rangel
DISCRETE
MATHEMATICS
MATH 170
PROJECT PART II
Jose De
Jesus
Melendez
Carlos
Aguilar
Drake Jain
PROJECT PART II
Section 4.6: # 22,
Section 9.2: #33
Section 9.5: #10
Section 10.2: #9, 18
Section
4.6
INDIRECT ARGUMENT:
CONTRADICTION AND
CONTRAPOSITION
WHAT IS ARGUMENT BY
CONTRADICTION?
Indirect proof
It is a statement that is either true or
false but not both
Reduces assumption by reasoning to a
contradiction
METHOD OF PROOF BY CONTRADICTION
1. Suppose that the statement that has to
be proved is false.
2. Logically, show that it leads to a
contradiction
3. Conclude that the statement that has to
be proved is true
EXAMPLE OF CONTRADICTION
Prove: For all integers x and y, x² ≠8y+2
So we must suppose that what we went to prove is false .
Suppose there are integer x and y such that x² =8y+2
Then x²= 2 4y + 1 . So x² is even.
X is also even, so x=2k for some integer k.
Then x²=4x²
We have 4x²=2 4y + 1 ≡ 2x²= 4y + 1
2x² is even and 4y + 1 is odd, so they can’t be equal.
Thus we have a contradiction, so there must not be any integers
x and y such that x²=8y+2
WHAT IS ARGUMENT BY
CONTRAPOSITION?
Form of indirect argument
Logical equivalence between statement
& its contrapositive
STEPS TO PROVE BY CONTRAPOSITION
Take contrapositive of statement
Prove contrapositive by direct proof
Conclude that original statement is true
EXAMPLE OF CONTRAPOSITION
∀x in D, if P(x)  Q(x).
Take contrapositive:
∀x in D, if ~Q(x)  ~P(x).
QUESTION 22
Consider the statement:
“For all real numbers r, if r² is irrational then r
is irrational.”
a) Write what you would suppose and what you
would need to show to prove this statement
by contradiction.
b) Write what you would suppose and what you
would need to show to prove this statement
by contraposition.
a) “For all real numbers r, if r² is irrational then r is irrational.”
∀x ∈ ℝ, 𝑟 2 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 → 𝑟 𝑖𝑠 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 .
Proof by contradiction: Suppose not. That is, suppose that there is a real number
r such that r² is irrational and r is rational. Show that this supposition leads
logically to a contradiction.
Contradiction: ∃𝑥𝜖ℝ, 𝑟 2 𝑖𝑠 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 → 𝑟 𝑖𝑠 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙
Let r²= 2
So, if r²=√2, then r= √(√2)
Statement is false. Original statement is true done by contradiction.
SUMMARY
 ∀x ∈ ℝ, 𝑟 2 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 → 𝑟 𝑖𝑠 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 .
To prove by contradiction, we must assume that what we went
to prove is false.
So we suppose that there exist a real number that if
𝑟 2 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 then 𝑟 𝑖𝑠 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙
So when we let Let r²=√2, r= √(√2) was not rational.
Hence, we have a contradiction.
b) “For all real numbers r, if r² is irrational then r is irrational.”
∀x ∈ ℝ, 𝑟 2 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 → 𝑟 𝑖𝑠 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙
Proof by contraposition: Suppose that r is a real number such that r is irrational.
Show that r² is not irrational.
Contraposition: ∃𝑥𝜖ℝ, 𝑟 2 𝑖𝑠 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 → 𝑟 𝑖𝑠 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙
Let r= a/b, a= 2 and b= 3
So, if r= 2/3 then r²= 4/9
Since r is rational, r² is rational.
Original statement is true done by contraposition.
Section
9.2
MULTIPLICATION RULE
THE MAN BEHIND THE COUNTING
Pierre-Simon Laplace
Mathematician and astronomer
His work led to the development
of mathematical astronomy and
statistics
There was no early biography of
Laplace
Starring mathematical physicist
between Newton and Maxwell
MULTIPLICATION RULE
If the operation consists of k steps and
- The first step can be performed in 𝑛1 ways
- The second step can be performed in 𝑛 2 ways
.
.
.
- The kth step can be performed in 𝑛 𝑘 ways
Then the entire operation can be performed in
𝑛 1 𝑛 2    𝑛 𝑘 ways.
- Discrete Mathematics (Susanna S. Epp)
HOW TO DO IT
 Example: How many 4 -digit PIN (Personal Identification Number)
numbers are there to create?
1 . Look for how many spaces you have
____ ____ ____ ____
In this case, you have 4.
2. Look at how many digits you can choose from.
0 1 2 3 4 5 6 7 8 9
Overall, you have 10 digits to choose from (including the
endpoints). So each space gets to have a choice of the 10
digits.
HOW TO DO IT (CONT’D)
3. Plug it in.
_10_ _10_ _10_ _10_
4. Multiply the spaces.
_10_ x _10_ x _10_ x _10_
5. There your number of possible PIN numbers
10 4 = 10000
6. DONE!
TRY IT
Section 9.2 #33
- Six people attend the theater together and sit in a row with
exactly six seats.
a. How many ways can they be seated together in the
row?
b. Suppose one of the six is a doctor who must sit on the
aisle in case she is paged. How many ways can the
people be seated together in the row with the doctor
in an aisle seat?
c. Suppose six people consist of three married couples
and each couple wants to sit together with the
husband on the left. How many ways can the six be
seated together in the row?
SOLUTION
a. How many ways can they be seated together in the row?
1 . How many spaces?
-6
2. How many to choose from?
-6
3. Plug it in.
_6_ _5_ _4_ _3_ _2_ _1_
The reason why each space decrease because as each
seat is taken, the person who sat down is pulled from the
situation.
4. Multiply.
6x5x4x 3x 2x 1
5. Answer: 720 ways (or you could leave it as “6 x 5 x 4 x 3 x 2 x
1”)
SOLUTION
b. Suppose one of the six is a doctor who must sit on the aisle
in case she is paged. How many ways can the people be seated
together in the row with the doctor in an aisle seat?
1 . How many spaces?
- 5, because the doctor already occupies a seat
2. How many to choose from?
-5
3. Plug it in.
_1_ _5_ _4_ _3_ _2_ _1_
4. Multiply.
1x5x4x 3x 2x 1
5. Answer: 120 ways
SOLUTION
c. Suppose six people consist of three married couples and each
couple wants to sit together with the husband on the left. How
many ways can the six be seated together in the row?
1 . How many spaces?
- 3, because a couple can occupy two seats the number
is reduced to half.
2. How many to choose from?
- 3, because a couple counts as 1 person now
3. Plug it in.
_3_ _2_ _1_
4. Multiply.
3x2x1
5. Answer: 6 ways
Section
9.5
COUNTING SUBSETS OF
A SET: COMBINATIONS
INFORMATION TO KNOW:
Formula: C (n, k ) =

𝑛
𝑘
=
𝑛!
𝑘! 𝑛−𝑘 !
𝑛
𝑘
, means “n chose k” = number of subset of size k
that can be chosen from n elements.
 n = total number of elements with-in a set
 k = total that are chosen from the set
 Where n and k are both nonnegative integers with
k ≤ n.
When C(n, 0) :
By definition 0! =1. Therefore, if k is zero and n
𝑛
0
is any nonnegative integer, then
is the
number of elements with-in the set of n.
C(n, 0) =
=
𝑛!
(1)∗𝑛!
𝑛
0
=1
=
𝑛!
0! 𝑛−0 !
EXAMPLE:
CSUMB has created an indoor -soccer league where teams of 6
(or 6-combination) members must be formed. If there are 31
people who want to play how many teams can be formed?
n = 31 people who want to play
k = 6 people per team
C(31 , 6) =
31
6
=
=
31!
6! 25 !
=
31∗30∗29∗28∗27∗26
6∗5∗4∗3∗2∗1
=
31!
6! 31−6 !
31∗30∗29∗28∗27∗26∗25!
6 ∗5∗4∗3∗2∗1 !25!
= 736,281 dif ferent teams can be formed.
QUESTION 10
Two new drugs are to be tested using
a group of 60 laboratory mice, each tagged with a number
for identification purposes. Drug A is to be
given to 22 mice, drug B is to be given to another 22 mice,
and the remaining 16 mice are to be used as controls. How
many ways can the assignment of treatments to mice be
made? (A single assignment involves specifying the
treatment for each mouse—whether drug A, drug B, or no
drug.)
Solution: Total Mice = 60 = n
Drug A = 22 mice = k (60¦22)
Drug B = 22 mice = k (38¦22)
Control = 16 = k (16¦16)
Drug A + Drug B + Control
60
22
+
=
38
22
+
60!
22! 38!
16
16
+
60!
22! 60−22 !
38!
16!
+
22!16!
16!0!
=
+
38!
22! 38−22 !
+
16!
16! 16−16 !
=
60∗59∗59∗58∗57∗57∗56∗56∗54∗53∗52∗51∗50∗49∗48∗47∗46∗45∗44∗43∗42∗41∗40∗39∗38!
22∗21∗20∗19∗18∗17∗16∗15∗14∗13∗12∗11∗10∗9∗8∗7∗6∗5∗4∗3∗2∗1! 38!
+
38∗37∗36∗35∗34∗33∗32∗31∗30∗29∗28∗27∗26∗25∗24∗23∗22!
22!16∗15∗14∗13∗12∗10∗11∗9∗8∗7∗6∗5∗4∗3∗2∗1!
= 5,848,876,094,823,595 + 22,239,974,430 + 1
= 5,848,898,334,807,026
+
16!
16!0!
SUMMARY
This question can be solved as an inclusion/exclusion problem. That
is because in the problem is states “A single assignment involves
specifying the treatment for each mouse”, therefore no mouse can be
given more than one drug type. Thus leading it to be and
inclusion/exclusion problem, in which this case it is an exclusion
problem where the number of elements is reduced for each subset
(here the subsets are Drug A, Drug B, and Control).
Therefore, you start with 60 mice total (n), and 22 mice (k) are to be chosen
to be in the first subset (Drug A).
So, Drug A= C(60, 22)
Since the first combination has taken
away 22 mice from the entire set (n), the
second subset (Drug B) only has 38 mice (n) in
which 22 mice (k) can be chosen.
So, Drug B= C(38, 22)
Finally for the last subset, since both first subset (Drug A) and the second
subset (Drug B) have used up 44 mice out of the 60 total. The last subset
(Control) is left with 16 mice (n) in which they can chose 16 (k) to have in the
Control group.
So, Control= C(16, 16) therefore there is only 1 combination for this subset.
Section
10.2
TRIALS, PATHS,
CIRCUITS
INFORMATION TO KNOW:
Walk:
An edge can be repeated, as well as vertices, and also the graph
does not have not be connected.
Trial:
Edges cannot be repeated, but vertices can be repeated.
Path:
Edges, and vertices cannot be repeated, and so one cannot end at
the same point they started with.
Closed Walk:
Edges and vertices can be repeated and you can end at the same
point you started with.
Circuit:
Edges cannot be repeated, but vertices can, also you can end at
the same point you started with.
INFORMATION TO KNOW:
Simple Circuit:
Edges cannot be repeated, and only the first and last vertex can
be repeated, therefore you can start and end at the same
vertex.
Euler’s Circuit:
A Euler Circuit can be made when a graph is connected (all
vertices are connected to one another by an edge) and the
degree of every vertex of the graph has a positive even degree.
Hamiltonian Circuit:
Is an simple circuit that contains every vertex in the graph, in
which every vertex appears only once excluding the first and
last vertex which are resulting to be the same.
EXAMPLE
 Does the following graph have a Euler’s circuit?
SOLUTION
Yes it does because the graph is connected and also
each vertex has a degree of positive even integer.
Therefore, the Euler circuit is
𝑉2 𝐸1 𝑉1 𝐸8 𝑉4 𝐸7 𝑉5 𝐸6 𝑉4 𝐸5 𝑉3 𝐸4 𝑉2
9. DOES THE GRAPH HAVE AN EULER
CIRCUIT? JUSTIFY YOUR ANSWERS.
A) G is a connected graph with five vertices of
degrees2,2,3,3, and 4.
B) B) G is a connected graph with five vertices of degrees
2,2,4,4, and 6.
C) C) G is a graph with five vertices of degrees 2,2,4,4,
and 6.
SOLUTION:
 A) No this graph G isn’t a Euler circuit, however it is a
Euler path.
 B) Yes by Euler’s theorem 10.2.3, the connected graph G
is a Euler circuit.
 C) Not necessary, because we do not know if the graph is
connected or not.
SUMMARY:
In Euler’s theorem 10.2.3 it states hat a connected graph G has
a Euler circuit if all the vertices have a even positive degree.
with this being said the graph mush be connected as well with
all even degrees. also it is possible to have a Euler path if there
is two degrees of odd integers from Euler’s theorem 10.2.4 is
states that a connected graph G can be an Euler path if and
only if there are exactly two vertices that are odd positive
integers.
A) This is not a Euler circuit, but a Euler path.10.2.4 Euler’s theorem states that a
connected graph G contains a Euler path if and only if there are exactly two
vertices with odd degrees. Graph G with degrees of 2,2,3,3,and 4 contains exactly
two degrees of odd integers.
B) Yes by Euler’s theorem this is a circuit because all the degrees are even integers
and the graph is connected. The theorem states that the graph must be connected
and contain vertices with all even degrees. the statement states that the graph G
is connected and has five vertices of all even integers 2,2,4,4, and 6.
C) The reason why the answer to the statement is not necessarily is because
the Euler theorem 10.2.3 states that the graph is connected. and the
statement does not state that the graph is connected but it does state that
there are five vertices with degrees of 2,2,4,4, and 6 even though the
theorem states “if and only if the vertices are all even degrees” it still states
that the graph G is connected. This statement has nothing about the graph
being connected or not so with that being said we can say not necessarily.
There is not enough information provided with it besides that all vertices
are even.
QUESTION 18
Is it possible to take a walk around the city whose map is shown
below, starting and ending at the same point and crossing each
bridge exactly once? If so, how can this be done?
SOLUTION
The way that this can be answered
is by the following circuit:
B →D→C→A→D→E→A→B
SUMMARY:
This question is looking for a Euler’s circuit that is because
which can be applied by Theorem 10.2.3, there are five edges
who’s each degree is of even amount. Therefore, since with-in
an Euler’s circuit every vertex has a degree of even amount.
Which by the map vertex B(2), D(4), C(2), A(4), D(4), E(2).
Which means a Euler’s circuit can be made.
•Therefore, you start with B and the use the first bridge to D.
So, B→D
•Since D has an even amount of bridges connecting to it (degree
amount) you can connect to either A, C or E.
So, D→C
•Since, C also has an even amount of bridges connecting to it
(degree amount) you can connect to A, you cannot go back to D
because the problem states that you cannot repeat the bridge.
So, C→A
•Then,
From A since you have to get to E, you can either go to
D then E or just E.
So, A→D
•Finally, from D all that is left is to take the bridge to E and
then to A, and one more bridge up to B.
So, D→E→A→B
•Therefore, the answer is:
B →D→C→A→D→E→A→B
BIBLIOGRAPHY
 Epp, Susanna S. Discrete Mathematics With Applications 4 th
Edition. Boston, MA: Brooks/Cole Publishing Company, 2004.
Print.
 Rowlinson, J. S. "Laplace: The Man." Notes and Records of the
Royal Society 60.2 (2006): 221-223.