fermat`s little theorem - University of Arizona Math
... Euclid’s division algorithm. Also, the foundation set by the Fundamental Theorem of Arithmetic was an essential tool in the sense that anticipating and predicting other larger numbers necessitates utilizing prime factorization to logically simplify the process. Around 300 BC, Euclid had written a ma ...
... Euclid’s division algorithm. Also, the foundation set by the Fundamental Theorem of Arithmetic was an essential tool in the sense that anticipating and predicting other larger numbers necessitates utilizing prime factorization to logically simplify the process. Around 300 BC, Euclid had written a ma ...
The Rabin-Miller Primality Test - University of San Diego Home Pages
... In fact, there are only 585,355 Carmichael numbers less than 1017. Given a randomly chosen odd integer n less than 1017, the probability that n is a Carmichael number is only a little over 10−11 (about one in one hundred billion). For a randomly chosen odd integer n with 100 to 300 digits, the proba ...
... In fact, there are only 585,355 Carmichael numbers less than 1017. Given a randomly chosen odd integer n less than 1017, the probability that n is a Carmichael number is only a little over 10−11 (about one in one hundred billion). For a randomly chosen odd integer n with 100 to 300 digits, the proba ...
Past Papers for “Discrete” Courses
... Those three courses have different emphases on techniques, but their syllabi have a considerable overlap of topics. Discrete mathematics tends to be very different from calculus, statistics and linear algebra. In discrete mathematics, very often, no systematic procedure can be applied, so one has to ...
... Those three courses have different emphases on techniques, but their syllabi have a considerable overlap of topics. Discrete mathematics tends to be very different from calculus, statistics and linear algebra. In discrete mathematics, very often, no systematic procedure can be applied, so one has to ...
leibniz, bernoulli and the logarithms of negative numbers
... common logarithm of a number is the Index of that power of 10 which is equal to the number.” Only a few years after this, Euler would also define logarithms in terms of exponents in his Introductio in Analysin written in 1745 and published in 1748. Between 1745 and 1749, Euler both corresponded with ...
... common logarithm of a number is the Index of that power of 10 which is equal to the number.” Only a few years after this, Euler would also define logarithms in terms of exponents in his Introductio in Analysin written in 1745 and published in 1748. Between 1745 and 1749, Euler both corresponded with ...
The Abundancy Index of Divisors of Odd Perfect Numbers
... is an odd perfect number and qi αi ||N ∀i, then the quantity ρi = σ(N/qi αi )/qi αi is an integer (because gcd(qi αi , σ(qi αi )) = 1). Suppose ρi = 1. Then σ(N/qi αi ) = qi αi and σ(qi αi ) = 2N/qi αi . Since N is an odd perfect number, qi is odd, whereupon we have an odd αi by considering parity c ...
... is an odd perfect number and qi αi ||N ∀i, then the quantity ρi = σ(N/qi αi )/qi αi is an integer (because gcd(qi αi , σ(qi αi )) = 1). Suppose ρi = 1. Then σ(N/qi αi ) = qi αi and σ(qi αi ) = 2N/qi αi . Since N is an odd perfect number, qi is odd, whereupon we have an odd αi by considering parity c ...
Polar and exponential forms
... We can write 1 − i in exponential form as p 7π 1 − i = 2e 4 i Raising both sides to the power of 4: (1 − i)4 ...
... We can write 1 − i in exponential form as p 7π 1 − i = 2e 4 i Raising both sides to the power of 4: (1 − i)4 ...
IOSR Journal of Mathematics (IOSR-JM) ISSN: 2278-5728. www.iosrjournals.org
... finding widest applications in all most all branches of Sciences, Social Sciences, Engineering, Computer Science, etc. Number Theory is one of the oldest branches of Mathematics, which inherited rich contributions from almost all greatest mathematicians, ancient and modern. Using the number theoreti ...
... finding widest applications in all most all branches of Sciences, Social Sciences, Engineering, Computer Science, etc. Number Theory is one of the oldest branches of Mathematics, which inherited rich contributions from almost all greatest mathematicians, ancient and modern. Using the number theoreti ...
Gabriel Lamé`s Counting of Triangulations
... problem of counting the number of triangulations of a convex polygon. Euler, one of the most prolific mathematicians of all times, and Goldbach, who was a Professor of Mathematics and historian at St. Petersburg and later served as a tutor for Tsar Peter II, carried out extensive correspondence, mos ...
... problem of counting the number of triangulations of a convex polygon. Euler, one of the most prolific mathematicians of all times, and Goldbach, who was a Professor of Mathematics and historian at St. Petersburg and later served as a tutor for Tsar Peter II, carried out extensive correspondence, mos ...
THE SOLOVAY–STRASSEN TEST 1. Introduction
... can be made into a deterministic primality test if we assume the truth of one of the most difficult unsolved problems in mathematics, called the Generalized Riemann Hypothesis (for Dirichlet L-functions). We will not explain here the Generalized Riemann Hypothesis, often abbreviated to GRH, but here ...
... can be made into a deterministic primality test if we assume the truth of one of the most difficult unsolved problems in mathematics, called the Generalized Riemann Hypothesis (for Dirichlet L-functions). We will not explain here the Generalized Riemann Hypothesis, often abbreviated to GRH, but here ...
Document
... All the elements of S are integers less than n that are relatively prime to n because a is relatively prime to n and xi is relatively prime to n, axi must also be relatively prime to n. There are no duplicates in S. If axi mod n = axj mod n, then xi = xj. by cancellation law. ...
... All the elements of S are integers less than n that are relatively prime to n because a is relatively prime to n and xi is relatively prime to n, axi must also be relatively prime to n. There are no duplicates in S. If axi mod n = axj mod n, then xi = xj. by cancellation law. ...
Arc Length, Area, and the Arcsine Function Author(s): Andrew M
... Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at http://www.jstor.org/page/ info/about/policies/terms.jsp JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a ...
... Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at http://www.jstor.org/page/ info/about/policies/terms.jsp JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a ...
arXiv:math/0510054v2 [math.HO] 17 Aug 2006
... etc. follows easily by induction, if one multiplied many factors from the given expression. The remaining of the series, in which prime numbers are seen, I do not see. This can be shown in a most pleasant investigation, together with tranquil pastime and the endurance of pertinacious labor, all thre ...
... etc. follows easily by induction, if one multiplied many factors from the given expression. The remaining of the series, in which prime numbers are seen, I do not see. This can be shown in a most pleasant investigation, together with tranquil pastime and the endurance of pertinacious labor, all thre ...
Footballs and donuts in four dimensions
... using only hexagonal and pentagonal patches, we might want to use patches shaped like other polygons, such as triangles, squares, octagons, or decagons. The only constraint is that we still must stitch all these patches together to form a football. 2 As an example, we could have started with 6 squar ...
... using only hexagonal and pentagonal patches, we might want to use patches shaped like other polygons, such as triangles, squares, octagons, or decagons. The only constraint is that we still must stitch all these patches together to form a football. 2 As an example, we could have started with 6 squar ...
Topological Dynamics of Fluids
... that vortex lines move as if they were composed of fluid particles - in modern parlance, the vortex lines are ‘frozen in the fluid’. As Kelvin recognized, this means that all topological structures associated with the vorticity field are invariant: two closed vortex tubes remain linked for all time ...
... that vortex lines move as if they were composed of fluid particles - in modern parlance, the vortex lines are ‘frozen in the fluid’. As Kelvin recognized, this means that all topological structures associated with the vorticity field are invariant: two closed vortex tubes remain linked for all time ...
1 - Columbia Math Department
... Obviously we would like to find a much better lower bound for π(x) than log log x. The first proof of the infinitude of primes which allows us a substantively better bound is Euler’s proof P which can be found in his book Introduction to Analysis of the Infinite. Here he actually shows that p prime ...
... Obviously we would like to find a much better lower bound for π(x) than log log x. The first proof of the infinitude of primes which allows us a substantively better bound is Euler’s proof P which can be found in his book Introduction to Analysis of the Infinite. Here he actually shows that p prime ...
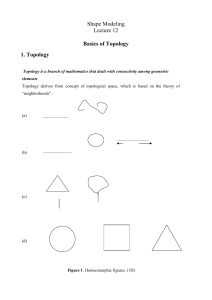
1. Topology
... In Figure 2 the figures are homeomorphic within each set, but not homeomorphic between ...
... In Figure 2 the figures are homeomorphic within each set, but not homeomorphic between ...
The Pentagonal Number Theorem and All That
... 28, 1741. Bernoulli is replying to a (lost) letter from Euler about the expansion, and he writes “The other problem, to transform (1 − x)(1 − x2 )(. . .) into 1 − x − x2 + x5 + . . ., follows easily by induction, if one multiplied many factors. The remainder of the series I do not see. This can be s ...
... 28, 1741. Bernoulli is replying to a (lost) letter from Euler about the expansion, and he writes “The other problem, to transform (1 − x)(1 − x2 )(. . .) into 1 − x − x2 + x5 + . . ., follows easily by induction, if one multiplied many factors. The remainder of the series I do not see. This can be s ...
SECTION 6.5: TRIG (AND EULER / EXPONENTIAL) FORMS OF A
... Again, see the Handout on my website. When we multiply complex numbers (in Trig Form), we multiply their moduli, but we add their arguments; we go one step down in the order of operations when we deal with arguments. You can see this from the Euler (Exponential) Form. When we divide complex numbers, ...
... Again, see the Handout on my website. When we multiply complex numbers (in Trig Form), we multiply their moduli, but we add their arguments; we go one step down in the order of operations when we deal with arguments. You can see this from the Euler (Exponential) Form. When we divide complex numbers, ...
PowerPoint 簡報 - National Chiao Tung University
... If n is an odd composite integer, then at most ¼ of all the numbers a, 1 ≦a ≦n-1 are strong liars for n. In fact if n=!9, then number of strong liars for n is at most Φ(n)/4. ...
... If n is an odd composite integer, then at most ¼ of all the numbers a, 1 ≦a ≦n-1 are strong liars for n. In fact if n=!9, then number of strong liars for n is at most Φ(n)/4. ...
Could Euler have conjectured the prime number theorem?
... sufficiently interested in the question of prime density; after all, as arguably the most prolific mathematician in history, he clearly had enough other things to occupy his attention! Indeed, his paper [Eul44] was not primarily about prime numbers, but rather about infinite series and their relatio ...
... sufficiently interested in the question of prime density; after all, as arguably the most prolific mathematician in history, he clearly had enough other things to occupy his attention! Indeed, his paper [Eul44] was not primarily about prime numbers, but rather about infinite series and their relatio ...
5.7 Euler`s Marvelous Formula (slides, 4-to-1)
... It is appropriate that we end our series of precalculus lectures with a presentation of Euler’s marvelous formula, which brings together both the trigonometric functions and the exponential functions into one form! The applications of this formula appear in all the technology around us, and simplify ...
... It is appropriate that we end our series of precalculus lectures with a presentation of Euler’s marvelous formula, which brings together both the trigonometric functions and the exponential functions into one form! The applications of this formula appear in all the technology around us, and simplify ...
euler student sample problems: solutions
... On the other hand, 5N = dy + 10 where y is an integer. Hence 5dx + 35 = dy + 10 which implies d(y − 5x) = 25. Thus 25 is divisible by d. ...
... On the other hand, 5N = dy + 10 where y is an integer. Hence 5dx + 35 = dy + 10 which implies d(y − 5x) = 25. Thus 25 is divisible by d. ...
Exponential Form of a Complex Number Lab
... efore we can investigate the exponential form of a complex number, we'll have to do some preliminary work. Much of it is based on work done by the remarkable mathematician Leonard Euler. We are first going to define the number e (through the use of the binomial theorem). Then, with the help of Euler ...
... efore we can investigate the exponential form of a complex number, we'll have to do some preliminary work. Much of it is based on work done by the remarkable mathematician Leonard Euler. We are first going to define the number e (through the use of the binomial theorem). Then, with the help of Euler ...
euler and the partial sums of the prime
... to arrange his ideas to prove the more precise claim that X ...
... to arrange his ideas to prove the more precise claim that X ...
QuestionFile3Cryptography
... a length of 200 decimal digits. Assume that you have sufficient secondary storage for them and that you can discount paging costs because you can prefetch the primes in order as needed. Then for some n <= 400 decimal digits in length, what would a simple brute force attack on an RSA encryption schem ...
... a length of 200 decimal digits. Assume that you have sufficient secondary storage for them and that you can discount paging costs because you can prefetch the primes in order as needed. Then for some n <= 400 decimal digits in length, what would a simple brute force attack on an RSA encryption schem ...
Leonhard Euler

Leonhard Euler (1707 – 1783) (/ˈɔɪlər/ OY-lər; German pronunciation: [ˈɔʏlɐ], local pronunciation: [ˈɔɪlr̩]) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function. He is also renowned for his work in mechanics, fluid dynamics, optics, astronomy, and music theory.Euler is considered to be the preeminent mathematician of the 18th century and one of the greatest mathematicians to have ever lived. He is also one of the most prolific mathematicians; his collected works fill 60 to 80 quarto volumes. He spent most of his adult life in St. Petersburg, Russia, and in Berlin, then the capital of Prussia.A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: ""Read Euler, read Euler, he is the master of us all.""










![arXiv:math/0510054v2 [math.HO] 17 Aug 2006](http://s1.studyres.com/store/data/014467696_1-4b3b027c0fc1865fd923af6e7da50abe-300x300.png)