Download Powerpoint ( file)


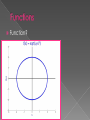
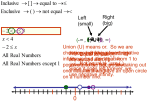
Email
› [email protected]
› If you are asking a question about the
WebAssign, for at least the next week or two
I will also need the problem

Website Materials
› www4.ncsu.edu/~jlwagne2/

Quizzes

Office Hours in Cox 502
› 1:15-2:15 on Thursday afternoons

MMC Hours
› 12-1 on Wednesdays
› 10-11 on Thursdays

Blue Books
› Need to bring in 5 of these
No laptops during class unless we are
discussing WebAssign.
 Please refrain from calling/texting.
 Please don’t pack up before you are
invited to do so.
 Please keep your work neat.

You can’t divide by 0. Even if you’re
Superman.
 (a+b)^2 is NOT (a^2+b^2). We rewrite it as
(a+b)(a+b) and realize that we need to FOIL
it to get a^2 + 2ab + b^2.
 a^0 is NOT 0. Anything to the 0th power is 1.

In technical terms, a function is a
relationship between a set of inputs and
outputs. The same input should not give
a different output, but different inputs
can result in the same output.
 We also say that x values aren’t allowed
to repeat, but y values are.


So knowing this, is this a function?
{(-3,9), (-2,4), (0,0), (1,1), (-3,8)}

So knowing this, is this a function?
{(-3,9), (-2,4), (0,0), (1,1), (-3,8)}
 No, because the x value
(“input”) of -3 gives 2 different y
values (“outputs”), 8 & 9.

Is this a function?
X
F(X)
1
2
2
4
3
2
4
3
5
1

Is this a function?
X
F(X)
1
2
2
4
3
2
4
3
5
1
 Yes, because each x value (“input”)
has one y value (“output”).

Vertical Line Test

Vertical Line Test
If you can draw
a vertical line
that passes over
the function
more than once
(anywhere!), the
graph is not of a
function!

Function?

Function?
Yes, because
at any point,
a vertical line
would not
cross the
graph more
than once.

Function?

Function?
No! Because
here the line
crosses our
graph twice.
To determine the domain of a function,
we need to figure out for what x values
the function exists.
 Also, what “input” values would be
unable to give us an “output” value?


The main things to keep in mind:
› Negative square roots are undefined.
› No matter how cool you are, you cannot
divide by zero.
› If neither one of these is applicable, consider
the possibility of “all real numbers” being
your answer.
On the other hand, range is the interval
of y values which are possible to get
from the function.
 Or, the possible “outputs” no matter
what “inputs” you put in.


Things to think about with range:
› Squared things are always greater than or
equal to 0.
› Square roots are always greater than or
equal to 0.

So what are the domain and range of
this function?

First…Domain
› Note the square root.
› So
x-2 >= 0.
x >= 2.
› We can also write [2,infinity).

Now range.
› We know that the square root will return an
answer greater than or equal to 0.
› Therefore, our range is y>=0, or [0,infinity).
We can
graph this to
check our
answer.
Domain:
 Fraction so you should think about NOT
dividing by zero
x-8 /= 0
x /= 8
 Other final answers include:
(-infinity,8)U(8,infinity)
or
all real numbers except 8
Range:
 Are there any squares or square roots? No.
 Think about the two pieces of the domain
we’ll input.
 Values bigger than 8 will give a positive
answer.
 Values smaller than 8 will give a negative
one.
 Can we get 0? Not possible.
 Our range is all real numbers except 0.
Graph to
confirm.
When we evaluate a function, we plug
something in for x. This doesn’t
necessarily have to be a number, but it
often is.
 To help avoid sign issues, ALWAYS use
parentheses around your substitution.

So what is f(0)?
So what is f(0)?
f(0)=(0)^2 + 3(0) – 2 = -2
So what is f(2)?
So what is f(2)?
f(2)=(2)^2 + 3(2) – 2
=4 + 6 – 2 = 8
So what is f(-x)?
So what is f(-x)?
f(-x)=(-x)^2 + 3(-x) – 2
= x^2 – 3x – 2