* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 1 - Dr. ZM Nizam
Shape-memory alloy wikipedia , lookup
Creep (deformation) wikipedia , lookup
Dislocation wikipedia , lookup
Fracture mechanics wikipedia , lookup
Mohr's circle wikipedia , lookup
Hooke's law wikipedia , lookup
Viscoplasticity wikipedia , lookup
Strengthening mechanisms of materials wikipedia , lookup
Cauchy stress tensor wikipedia , lookup
Deformation (mechanics) wikipedia , lookup
Stress (mechanics) wikipedia , lookup
Work hardening wikipedia , lookup
Fatigue (material) wikipedia , lookup
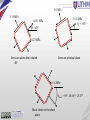
BFC 20903 (Mechanics of Materials) Chapter 1: Stress & Strain Shahrul Niza Mokhatar [email protected] Chapter Learning Outcome 1. Defined the relationship between stress and strain 2. Analyse the stress and strain using related equations 3. Determine and analyse the deformation of a rod of uniform or variable cross section under one or several load 4. Determine the principal stress using equation and Mohr’s circle method BFC 20903 (Mechanics of Materials) Shahrul Niza Mokhatar ([email protected] Introduction • Mechanics of materials is a branch of mechanics that studies the internal effects of stress and strain in a solid body that is subjected to an external loading. • Stress is associated with the strength of the material from which the body is made. • Strain is a measure of the deformation of the body. Type of forces • Normal force, N – Acts perpendicular to the area. – Developed when the external loads to push or pull on the two segments of the body • Shear force, V – Shear force lies in the plane of the area. – Developed when the external loads tend to cause the two segments of the body to slide. Type of forces • Torque or torsional moment, T - Developed when the external loads tend to twist one segments of the body with respect to the other. • Bending moment, M - Cause by the external loads that tend to bend the body about an axis within the plane of the area. Stresses • Stress is the internal force exerted by one part of an elastic body upon the adjoining part. • Stress has a dimension of Newton/m2 • Generally, they are 6 independent components of stress at each point. or Type of stress • Type of stress – Normal stress or uniaxial stress, σ - stress is evenly distributed over the entire cross-section. • Normal stress includes tensile and compressive stress F A – Shear stress, τ – results when a force tends to make part of the body or one side of a plane slide past the other. F A Type of stress: Shear Stress F 2A F A Type of stress: Bearing Stress Bearing stress, τ – Bearing stress is a type of normal stress but it involves the interaction of two surfaces. The bearing stress is the pressure experience by the second surface due to the action from the first surface. Example: the pressure between bolt and plate at a joint. F F A tD Example 1 Example 2 Example 2: Solution Example 3 Example 3: Solution Quiz 1 : Shear Stress Quiz 1: Solution Strain • Measure of deformation representing the displacement between particles in the body relative to a reference length. • Ratio of change in length due to deformation to the original length. • It is dimensionless quantity. • Numerical values of strain are usually very small, especially for structural materials, which ordinarily undergo only small changes in dimensions. Types of Strain • Normal strain - Normal strain (ε) is the deformation of a body which involved elongation or contraction. • When a bar of length L and cross-sectional area A is subjected to axial tensile force P through the crosssection's centroid, the bar elongates. • The change in length divided by the initial length is the bar's engineering strain. The symbol for strain is ε (epsilon). The strain in an axially loaded bar is: L Types of Strain • Shear strain - Shear strain is a strain which involved a shear deformation i.e. body twist due to torsion and a distorted cuboid as shown in Figure 1.8. Strain changes the angles of an object and shear causes lines to rotate. aa' L Stress & Strain relationships Stress & strain relationships Elastic Proportional Limit (Hooke's Law) From the origin O to the point called proportional limit, the stress-strain curve is a straight line. Stress & Strain relationships • • • • • Elastic Limit The elastic limit is the limit beyond which the material will no longer go back to its original shape when the load is removed, or it is the maximum stress that may be developed such that there is no permanent or residual deformation when the load is entirely removed. Yield Point/ Yield Strength Yield point is the point at which the material will have an appreciable elongation or yielding without any increase in load. The material is said to undergo plastic deformation. Strain hardening Point C to D is called as strain hardening region whereas the curve rises gradually until it flatten at D. The stress which correspond to point D is called ultimate strength/stress Ultimate Strength/Stress The maximum ordinate in the stress-strain diagram is the ultimate strength or tensile strength. Rapture Strength (Fracture) Rapture strength is the strength of the material at rupture. This is also known as the breaking strength (final point). Offset method • Beside steel, other materials such as aluminium, glass, brass and zinc, constant yielding will not occur beyond the elastic range. This metal often does not have a well defined yield point. Therefore, the standard practice to define yield strength for this metal is graphical procedure called the offset method. Normally a 0.2% (0.002 mm/mm) is chosen, and from this point on the strain (ε) axis, a line parallel to the initial straight-line portion of the stress-strain diagram is drawn. The point where this line intersects the curves defines the yield strength. Example 5 Example 5: Solution From the graph: (a) E = 112.07/0.00125 (b) σy = 230 N/mm2 (c) σmax = 270 N/mm2 Hooke’s Law • Stiffness; Modulus Young Stiffness is a material's ability to resist deformation. The stiffness of a material is defined through Hooke's Law. • Young's Modulus is the slope of the linear-elastic region of the stress-strain curve. Hooke’s Law E • where E is Young's Modulus (the modulus of elasticity), a material property. Values of E for different materials are obtained experimentally from stress-strain curves. • From Hooke’s Law, the displacement can be derived: • Consider a homogenous rod BC of length L and uniform cross section of area A subjected to a centric axial load P (Figure). If the resulting axial stress σ = P/A does not exceed the proportional limit of the material, the Hooke’s law can be apply and write as follow: Poisson ratio • Poisson's ratio is the ratio of lateral contraction strain to longitudinal extension strain in the direction of stretching force. • Tensile deformation is considered positive and compressive deformation is considered negative. The definition of Poisson's ratio contains a minus sign so that normal materials have a positive ratio. Poisson's ratio, also called Poisson ratio or the Poisson coefficient. Poisson's ratio is a materials property. lateral logitudinal Example 6 Working stress, permissible stress and temperature stress • Temperature stress An object will expand when heated and contract when the temperature drops. Since this is the effect of temperature on the member then the corresponding stress and strain are called temperature stress and temperature strain. The variation of the length due to temperature change depends upon its coefficient of linear expansion or contraction α where α is the change in length for a unit change of temperature per unit original length. Example 7: Tutorial Example 7 : Solution Assignment 1: Individu Plane Stress and Mohr Circle Stress Analysis Using Equation and Mohr Diagram Method Rotation angle, θ Clockwise –ve Counterclockwise +ve • Principal stresses occur on the principal planes of stress with zero shear stress • Maximum shearing stress • Normal stress on the y’ and x’axis • Shear stress corresponds to x’ and y’ Example 8 For the state of plane stress shown, determine (a) the principal stress (b) principal planes (c)maximum shear stress Example 8: Solution Example 9: Tutorial The state of plane stress at a failure point on shaft as shown in Fig. Represent this stress state in terms of its principal stresses Example 9: Solution • From the established sign convention, we have σx = -20 MPa, σy = 90 MPa, τxy = 60 MPa • Orientation of element tan 2 p 2 xy x y 2(60) 47.49 0 p 2 23.7 0 (20 90) • Recall that θ must be measured positive counterclockwise from the x axis to the outward normal (x’ axis) on the face of the element. Example 9: Solution • Principal stress max, min 2 x y 20 90 x y 2 xy 2 2 2 max 116 MPa 20 90 2 60 2 min 46.4MPa 2 Example 9: Solution • The principal plane on which each normal stress acts can be determined with θp2 = -23.70 x y x y x' cos 2 xy sin 2 2 2 20 90 20 90 x' cos 2(23.70 ) 60 sin 2(23.70 ) 2 2 x ' 46.4MPa Example 10 The state of plane stress at a point on a body is represented on the element as shown in Fig. Represent this stress state in terms of maximum in-plane shear stress and associated average normal stress •From the established sign convention, we have σx = -20 MPa, σy = 90 MPa, τxy = 60 MPa Example 10: Solution • Orientation of element x y (20 90) tan 2 s 2 42.50 s 2 21.30 2 xy 2(60) • Note how these angles are formed between x and x’ axes. • Maximum in-plane shear stress max 2 x y 2 xy 2 20 90 2 (60) 2 2 81.4MPa • The shear stress corresponding to θs2 = 21.30 can be determined by x y xy ' sin 2 xy cos 2 2 xy ' 20 90 sin 2(21.30 ) 60 cos 2(21.30 ) 81.4MPa 2 • This positive result indicates that τmax = τxy’ acts in the positive y’ direction on this face (θ = 21.30). • Average normal stress avg x y 2 20 90 35 MPa 2 Mohr Circle • Mohr’s circle can be used to determine the principal stresses, the maximum in-plane shear stress and average normal stress or the stress on any arbitrary plane. • By adding and squaring each equation, the value of θ can be eliminated τ τ Mohr Circle: Two manners τ τ Example 11 Using Mohr’s cirlce method. Determine: (a) normal and shearing stresses after rotated 400 (b) principal stress (c) maximum shear stress Example 11: Solution • Determine the centre line, C and radius of Mohr’s circle R C= • Determine the coordinate A and A’ as a stress on x and y A (σ = 15 Mpa and τ = 4 Mpa) A’ (σ = 5 Mpa and τ = - 4 Mpa) τ (-ve) σmax = 16.4 σx‘ = 14.81 • S B A’ (5,- 4) tan 2θ = 4/5 = 38.660 θp = 19.330 • τxy = -4 60.670 Q P C 38.660 σmin = 3.6 σy’ = 5.19 Determine the angle of ACP, location of plane for the maximum stress B’ R Determine B as a plane of x’ corresponds to the angle of 400 2θ = 800 from A Angle BCP = 800- θp = 60.670 (a) So, stress on x’is point B and stress on y’is point B’ A (15, 4) σx’ = 10 + 6.4cos 41.340 = 14.81 MPa τx’y’ = -6.4sin 41.340 = -4.23 MPa σy’ = 10 - 6.4cos 41.340 = 5.19 MPa τx’y’ = 6.4sin 41.340 = 4.23 MPa σx= 15 τ (+ve) (b) Principal stress is point P and Q (c) Max shear stress is point S and R 3.6 MPa 5.19 MPa 16.4 MPa θp = 19.30 14.81 MPa θ = 400 4.23 MPa Stress on principal plane Stress on plane after rotated 400 6.4 MPa θsmax = 900 - 38.660 = 25.670 Shear stress on the shear plane - END -