Download Chapter 1 - Dr. ZM Nizam

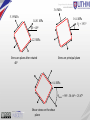
BFC 20903 (Mechanics of Materials)
Chapter 1: Stress & Strain
Shahrul Niza Mokhatar
[email protected]
Chapter Learning Outcome
1. Defined the relationship between stress and
strain
2. Analyse the stress and strain using related
equations
3. Determine and analyse the deformation of a
rod of uniform or variable cross section
under one or several load
4. Determine the principal stress using equation
and Mohr’s circle method
BFC 20903 (Mechanics of Materials)
Shahrul Niza Mokhatar ([email protected]
Introduction
• Mechanics of materials is a branch of mechanics that
studies the internal effects of stress and strain in a solid
body that is subjected to an external loading.
• Stress is associated with the strength of
the material from which the body is made.
• Strain is a measure of the deformation
of the body.
Type of forces
• Normal force, N
– Acts perpendicular to the area.
– Developed when the external loads to push
or pull on the two segments of the body
• Shear force, V
– Shear force lies in the plane of the area.
– Developed when the external loads tend to
cause the two segments of the body to slide.
Type of forces
• Torque or torsional moment, T
- Developed when the external loads tend to
twist one segments of the body with respect
to the other.
• Bending moment, M
- Cause by the external loads that tend to
bend the body about an axis within the
plane of the area.
Stresses
• Stress is the internal force exerted by one part of
an elastic body upon the adjoining part.
• Stress has a dimension of Newton/m2
• Generally, they are 6 independent components of
stress at each point.
or
Type of stress
• Type of stress
– Normal stress or uniaxial stress, σ - stress is
evenly distributed over the entire cross-section.
• Normal stress includes tensile and compressive
stress
F

A
– Shear stress, τ – results when a force tends to make part
of the body or one side of a plane slide past the other.
F

A
Type of stress: Shear Stress
F

2A
F

A
Type of stress: Bearing Stress
Bearing stress, τ – Bearing stress is a type of normal stress but it
involves the interaction of two surfaces. The bearing stress is the
pressure experience by the second surface due to the action
from the first surface. Example: the pressure between bolt and
plate at a joint.

F F

A tD
Example 1
Example 2
Example 2: Solution
Example 3
Example 3: Solution
Quiz 1 : Shear Stress
Quiz 1: Solution
Strain
• Measure of deformation representing the displacement
between particles in the body relative to a reference length.
• Ratio of change in length due to deformation to the original
length.
• It is dimensionless quantity.
• Numerical values of strain are usually very small, especially for
structural materials, which ordinarily undergo only small
changes in dimensions.
Types of Strain
• Normal strain - Normal strain (ε) is the deformation of
a body which involved elongation or contraction.
• When a bar of length L and cross-sectional area A is
subjected to axial tensile force P through the crosssection's centroid, the bar elongates.
• The change in length divided by the initial length is the
bar's engineering strain. The symbol for strain is ε (epsilon).
The strain in an axially loaded bar is:


L
Types of Strain
• Shear strain - Shear strain is a strain which involved a
shear deformation i.e. body twist due to torsion and
a distorted cuboid as shown in Figure 1.8. Strain
changes the angles of an object and shear causes
lines to rotate.

aa'
L
Stress & Strain relationships
Stress & strain relationships
Elastic Proportional Limit (Hooke's Law)
From the origin O to the point called proportional limit, the stress-strain curve is a straight
line.
Stress & Strain relationships
•
•
•
•
•
Elastic Limit
The elastic limit is the limit beyond which the material will no longer go back to its original
shape when the load is removed, or it is the maximum stress that may be developed such
that there is no permanent or residual deformation when the load is entirely removed.
Yield Point/ Yield Strength
Yield point is the point at which the material will have an appreciable elongation or
yielding without any increase in load. The material is said to undergo plastic deformation.
Strain hardening
Point C to D is called as strain hardening region whereas the curve rises gradually until it
flatten at D. The stress which correspond to point D is called ultimate strength/stress
Ultimate Strength/Stress
The maximum ordinate in the stress-strain diagram is the ultimate strength or tensile
strength.
Rapture Strength (Fracture)
Rapture strength is the strength of the material at rupture. This is also known as the
breaking strength (final point).
Offset method
• Beside steel, other materials such as aluminium, glass, brass and zinc, constant
yielding will not occur beyond the elastic range. This metal often does not have
a well defined yield point. Therefore, the standard practice to define yield
strength for this metal is graphical procedure called the offset method.
Normally a 0.2% (0.002 mm/mm) is chosen, and from this point on the strain
(ε) axis, a line parallel to the initial straight-line portion of the stress-strain
diagram is drawn. The point where this line intersects the curves defines the
yield strength.
Example 5
Example 5: Solution
From the graph:
(a) E = 112.07/0.00125
(b) σy = 230 N/mm2
(c) σmax = 270 N/mm2
Hooke’s Law
• Stiffness; Modulus Young Stiffness is a material's ability
to resist deformation. The stiffness of a material is
defined through Hooke's Law.
• Young's Modulus is the slope of the linear-elastic region
of the stress-strain curve.
Hooke’s Law
  E
• where E is Young's Modulus (the modulus of elasticity), a
material property. Values of E for different materials are
obtained experimentally from stress-strain curves.
• From Hooke’s Law, the displacement can be
derived:
• Consider a homogenous rod BC of length L and
uniform cross section of area A subjected to a
centric axial load P (Figure).
If the resulting axial stress σ = P/A does not exceed the
proportional limit of the material, the Hooke’s law can be
apply and write as follow:
Poisson ratio
• Poisson's ratio is the ratio of lateral contraction strain to
longitudinal extension strain in the direction of stretching
force.
• Tensile deformation is considered positive and compressive
deformation is considered negative. The definition of
Poisson's ratio contains a minus sign so that normal
materials have a positive ratio. Poisson's ratio, also called
Poisson ratio or the Poisson coefficient. Poisson's ratio is a
materials property.


lateral
 logitudinal
Example 6
Working stress,
permissible stress and temperature
stress
• Temperature stress
 An object will expand when heated and contract when the
temperature drops.
 Since this is the effect of temperature on the member then
the corresponding stress and strain are called temperature
stress and temperature strain.
 The variation of the length due to temperature change
depends upon its coefficient of linear expansion or
contraction α where α is the change in length for a unit
change of temperature per unit original length.
Example 7: Tutorial
Example 7 : Solution
Assignment 1: Individu
Plane Stress and Mohr Circle
Stress Analysis Using Equation and
Mohr Diagram Method
Rotation angle, θ
Clockwise –ve
Counterclockwise +ve
•
Principal stresses occur on the principal planes of stress with zero shear
stress
•
Maximum shearing stress
•
Normal stress on the y’ and x’axis
•
Shear stress corresponds to x’ and y’
Example 8
For the state of plane stress shown, determine
(a) the principal stress
(b) principal planes
(c)maximum shear stress
Example 8: Solution
Example 9: Tutorial
The state of plane stress at a failure point on shaft as shown in Fig.
Represent this stress state in terms of its principal stresses
Example 9: Solution
• From the established sign convention, we have
σx = -20 MPa, σy = 90 MPa, τxy = 60 MPa
• Orientation of element
tan 2 p 
2 xy
 x   y 

2(60)
 47.49 0   p 2  23.7 0
(20  90)
• Recall that θ must be measured positive counterclockwise
from the x axis to the outward normal (x’ axis) on the face of
the element.
Example 9: Solution
• Principal stress
 max, min
2
 x  y



 20  90
x
y 
2


 
   xy 
 2 
2
2
 max  116 MPa


 20  90
2
  60 
2
 min  46.4MPa
2
Example 9: Solution
• The principal plane on which each normal stress acts can be
determined with θp2 = -23.70
 x  y  x  y
 x' 

cos 2   xy sin 2
2
2
 20  90  20  90
 x' 

cos 2(23.70 )  60 sin 2(23.70 )
2
2
 x '  46.4MPa
Example 10
The state of plane stress at a point on a body is represented on the
element as shown in Fig. Represent this stress state in terms of
maximum in-plane shear stress and associated average normal
stress
•From the established sign convention, we have
σx = -20 MPa, σy = 90 MPa, τxy = 60 MPa
Example 10: Solution
• Orientation of element
  x   y   (20  90)
tan 2 s 2 

 42.50   s 2  21.30
2 xy
2(60)
• Note how these angles are formed between x and x’ axes.
• Maximum in-plane shear stress
 max
2



x
y 
2
 
   xy 

2


 20  90
2
  (60)
2
2
 81.4MPa
• The shear stress corresponding to θs2 = 21.30 can be determined by
 x  y 

 xy '  
 sin 2   xy cos 2


2
 xy '


 20  90

sin 2(21.30 )  60 cos 2(21.30 )  81.4MPa
2
• This positive result indicates that τmax = τxy’ acts in the positive y’ direction on
this face (θ = 21.30).
• Average normal stress
 avg 
 x  y
2

 20  90
 35 MPa
2
Mohr Circle
•
Mohr’s circle can be used to determine the principal stresses, the maximum in-plane
shear stress and average normal stress or the stress on any arbitrary plane.
•
By adding and squaring each equation, the value of θ can be eliminated
τ
τ
Mohr Circle: Two manners
τ
τ
Example 11
Using Mohr’s cirlce method. Determine:
(a) normal and shearing stresses after rotated 400
(b) principal stress
(c) maximum shear stress
Example 11: Solution
• Determine the centre line, C and radius of Mohr’s circle R
C=
• Determine the coordinate A and A’ as a stress on x and y
A (σ = 15 Mpa and τ = 4 Mpa)
A’ (σ = 5 Mpa and τ = - 4 Mpa)
τ (-ve)
σmax = 16.4
σx‘ = 14.81
•
S
B
A’ (5,- 4)
tan 2θ = 4/5 = 38.660
θp = 19.330
•
τxy = -4
60.670
Q
P
C
38.660
σmin = 3.6
σy’ = 5.19
Determine the angle of ACP,
location of plane for the maximum
stress
B’
R
Determine B as a plane of x’
corresponds to the angle of 400
2θ = 800 from A
Angle BCP = 800- θp = 60.670
(a) So, stress on x’is point B and
stress on y’is point B’
A (15, 4) σx’ = 10 + 6.4cos 41.340 = 14.81 MPa
τx’y’ = -6.4sin 41.340 = -4.23 MPa
σy’ = 10 - 6.4cos 41.340 = 5.19 MPa
τx’y’ = 6.4sin 41.340 = 4.23 MPa
σx= 15
τ (+ve)
(b) Principal stress is point P and Q
(c) Max shear stress is point S and R
3.6 MPa
5.19 MPa
16.4 MPa
θp = 19.30
14.81 MPa
θ = 400
4.23 MPa
Stress on principal plane
Stress on plane after rotated
400
6.4 MPa
θsmax = 900 - 38.660 = 25.670
Shear stress on the shear
plane
- END -