* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Experimental determination of natural frequency and damping ratio
Wave packet wikipedia , lookup
Brownian motion wikipedia , lookup
Center of mass wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Dynamic substructuring wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Routhian mechanics wikipedia , lookup
Hunting oscillation wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Work (physics) wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Centripetal force wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Spinodal decomposition wikipedia , lookup
Equation of state wikipedia , lookup
Seismometer wikipedia , lookup
Classical central-force problem wikipedia , lookup
UNIT 1
Oscillating Motions:
The study of vibrations is concerned with the oscillating motion of elastic bodies and the
force associated with them.
All bodies possessing mass and elasticity are capable of vibrations.
Most engineering machines and structures experience vibrations to some degree and their
design generally requires consideration of their oscillatory motions.
Oscillatory systems can be broadly characterized as linear or nonlinear.
Linear systems :
The principle of superposition holds
o Mathematical technique available for their analysis are well developed.
Nonlinear systems:
The principle of superposition doesn't hold
o
The technique for the analysis of the nonlinear systems are under development (or
less well known) and difficult to apply.
All systems tend to become nonlinear with increasing amplitudes of oscillations.
There are two general classes of vibrations– free and forced.
Free vibrations:
• Free vibration takes place when a system oscillates under the action of forces inherent in the
system itself due to initial disturbance, and when the externally applied forces are absent.
• The system under free vibration will vibrate at one or more of its natural frequencies, which
are properties of the dynamical system, established by its mass and stiffness distribution.
Forced vibrations:
The vibration that takes place under the excitation of external forces is called forced
vibration.
If excitation is harmonic, the system is forced to vibrate at excitation frequency. If the
frequency of excitation coincides with one of the natural frequencies of the system, a
condition of resonance is encountered and dangerously large oscillations may result,
which results in failure of major structures, i.e., bridges, buildings, or airplane wings etc.
Thus calculation of natural frequencies is of major importance in the study of vibrations.
Because of friction & other resistances vibrating systems are subjected to damping to
some degree due to dissipation of energy.
Damping has very little effect on natural frequency of the system, and hence the
calculations for natural frequencies are generally made on the basis of no damping.
Damping is of great importance in limiting the amplitude of oscillation at resonance.
Degrees of Freedom (dof):
The number of independent co-ordinates required to describe the motion of a system is
termed as degrees of freedom.
For example
Particle - 3 dof (positions)
Rigid body-6 dof (3-positions and 3-orientations)
Continuous elastic body - infinite dof (three positions to each particle of the body).
If part of such continuous elastic bodies may be assumed to be rigid (or lumped) and the
system may be considered to be dynamically equivalent to one having finite dof (or
lumped mass systems).
Large number of vibration problems can be analyzed with sufficient accuracy by
reducing the system to one having a few dof.
Vibration measurement terminology :
Peak value: Indicates the maximum response of a vibrating part. It also places a
limitation on the “rattle space” requirement.
Average value : Indicates a steady or static value (somewhat like the DC level of an
electrical current) and it is defined as
(1.1)
where x(t) is the displacement, and T is the time span (for example time period)
Example:
For a complete cycle of sine wave,
(1.2)
For half cycle of the sine wave :
where A is the amplitude of the displacement.
Mean square value: Square of the displacement generally is associated with the energy of the
vibration for which the mean square value is a measure and is defined as
(1.3)
Example : For a complete cycle of sine wave
, we have
(1.4)
Root mean square value (rms) : This is the square root of the mean square value.
For example : for a complete sine wave
(1.5)
Oscillatory Motion
Repeat itself regularly for example pendulum of a wall clock
Display irregularity for example earthquake
Periodic Motion – This motion repeats at equal interval of time T.
Period of Oscillatory – The time taken for one repetition is called period.
Frequency -
, It is defined reciprocal of time period.
The condition of the periodic motion is
(1.10)
where motion is designated by time function x(t)
Harmonic motion :
Simplest form of periodic motion is harmonic motion and it is called simple harmonic
motion (SHM). It can be expressed as
(1.11)
where A is the amplitude of motion, t is the time instant and T is the period of motion
Harmonic motion is often represented by projection on line of a point that is moving on a
circle at constant speed. (SHM Animation)
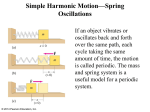
Figure 1.1: The Simple Harmonic Motion
From Figure 1.1 , we have
where x is the displacement and
is the circular frequency in rad/sec.
where T is the period (sec) and f is the frequency (cycle/sec) of the harmonic motion.
The SHM repeats itself in
radians.
Displacement can be expressed as
(1.12)
So that the velocity and acceleration can be written as
(1.13)
(1.14)
Equations (1.12) to (1.14) are plotted in Figure 1.2
Figure 1.2 : Variation of displacement, velocity and acceleration with nondimensional
time.
It should be noted from equations (1.12-1.14) that when displacement is a SHM the velocity and
acceleration are also harmonic motion with same frequency of oscillation (i.e. displacement).
However, lead in phases occurs by 900 and 1800 respectively with respect to the displacement as
shown in Figure 1.2.
From equations (1.12) and (1.14) we find
(1.15)
In harmonic motion acceleration is proportional to the displacement and is directed
towards the origin.
The Newton's second law of motion states that the acceleration is proportional to the
force. Hence for a spring (linear), we write
(1.16)
where FS is the spring force and k is the stiffness of the spring. It executes harmonic
motion as force is proportional to the displacement. (animation)
Exponential form : From Euler's equation, we have
(1.17)
A rotating vector can be expressed as
(1.18)
where A is the magnitude,
is the orientation and j =
Equation (1.18) can also be written as
is the imaginary number.
(1.19)
with
(1.20)
where z is the complex sinusoid, x is the real component and y is the imaginary
component.
Differentiating equation (1.18) with respect to time gives
(1.21)
and
(1.22)
From equation (1.19), we can write
(1.23)
where
is the complex conjugate of z as shown Figure 1.4. We can also write
(1.24)
where Re(z) is the real part of quantity z.
The exponential form of the harmonic motion offers mathematical advantages over the
trigonometric form.
Example 1.1 : A harmonic motion has an amplitude of 0.20 cm and a period of 0.15 sec.
Determine the maximum velocity and acceleration.
Solution : The frequecny is given as
The maximum velocity is given as
The maximum acceleration is given as
Exercise 1.1: Calculate the maximum acceleration (in units of g) of a pickup stylus
reproducing a frequency of 16 kHz; with an amplitude of 0.01 mm. [Ans: 10,302 g]
Exercise1.2: Calculate(a)the amplitude and(b) the phase constant for the vibration given
by
. [Ans: (a) 19.7 mm (b) -600 ]
UNIT 2
FREE VIBRATIONS
Objective of the present section will be to write the equation of motion of a system and
evaluate its natural frequency, which is mainly a function of mass,
stiffness, and damping of the system from its general solution.
In many pratical situation, damping has little influence on the natural frequency and may
be neglected in its calculation.
In absence of damping, the system can be considered as conservative and principle of
conservation of energy offers another approach to the calculation of the natural
frequency.
The effect of damping is mainly evident in diminishing of the vibration amplitude at or
near the resonance.
Vibration Model :
The basic vibration model consists of a mass, spring (stiffness) and damper (damping) as
shown in Figure 2.1
Figure 2.1: Spring-damper vibration model.
The inertia force model is
(2.1)
where m is the mass in kg,
is the acceleration in m/sec2 and Fi is the inertia force in N.
The linear stiffness force model is
Fs= kx
where k is the stiffness (N/m), x is the displacement and Fs is the spring force.
(2.2)
The damping force model for the viscous damping is
(2.3)
where c is the damping coefficient in N/m/sec,
force.
is the velocity in m/sec and Fd is the damping
Undamped Free Vibration
A spring mass system as shown in Figure 2.2 is considered. For simplicity at present the
damping is not considered.
The direction of x in the downward direction is positive. Also velocity,
force, F, are positive in the downward direction as shown in Figure 2.2.
, acceleration,
, and
From Figure 2.2(d) on application of Newton's second law, we have
or
From Figure 2.2(b), we have
(i.e. spring force due to static deflection is equal to
weight of the suspended mass), so the above equation becomes
(2.4)
The choice of the static equilibrium position as reference for x axis datum has eliminated the
force due to the gravity. Equation (2.4) can be written as
or
(2.5)
With
(2.6)
Where
is the natural frequency (in rads/sec). Equation (2.5) satisfies the simple harmonic
motion condition.
Solution of EOM:
From equation (2.5), it can be observed that
The motion is harmonic (i.e. the acceleration is proportional to the displacement).
It is homogeneous, second order, linear differential equation (in the solution two arbitrary
constants should be there).
The general solution of equation (2.5) can be written as
(2.7)
where A and B are two arbitrary constants, which depend upon initial conditions
i.e. x (0) and
. Equation (2.5) can be differentiated to give
(2.8)
On application of initial conditions in equation (2.7) and (2.8), we get
x (0) = B and
or
and
B = x(0 )
(2.9)
On substituting equation (2.9) into equation (2.8), we get
(2.10)
where,
where X is the amplitude,
is the circular frequency and
is the phase. The undamped free
vibration executes the simple harmonic motion as shown in Figure 2.3.
Since sine & cosine functions repeat after 2
have
radians (i.e. Frequency
Time period = 2
), we
(2.11)
The time period (in second) can be written as
(2.12)
The natural frequency (in rads/sec or Hertz) can be written as
(2.13)
From Figure 2.2(b), we have
(2.14)
On substituting equation (2.14) into equation (2.13), we get
Here T , f ,
system.
are dependent upon mass & stiffness of the system, which are properties of the
Above analysis is valid for all kind of SDOF system including beam or torsional members. For
torsional vibrations the mass may be replaced by the mass moment of inertia and stiffness by
stiffness of torsional spring. For stepped shaft an equivalent stiffness can be taken or for
distributed mass an equivalent lumped mass can be taken.
The undamped free response can also be written as
where A & B are constants to be determined from initial conditions, which is same as equation
(2.7).
Equivalent Stiffness of Series and Parallel Springs :
For this system having springs connected in series or parallel, equation (2.13) is still valid with
the equivalent stiffness as shown in Figures 2.4 and 2.5.
Figure 2.4
Figure 2.5
Equivalent Stiffness of a Cantilever Beam :
The deflection of a cantilever beam as shown in Figure 2.6 is given as
The equivalent stiffness is given as
is the deflection, E = Young's modulous, I = mass moment of inertia,
l = length of the beam, P is the load.
Similarly equivalent stiffness of a rod and shaft can be obtained considering axial force and torque respectively.
Equation (2.13) is valid for all these cases also.
Example 2.1 : Derive equation of motion of a simple pendulum for large and small oscillations.
Solution : Figure 2.7 shows a simple pendulum and free body diagram of the bob.
Tension in spring is given by
(a)
From Newton's second law the moment balance about centre of rotation O is given as
where I is the polar mass moment of inertia, of the mass m about centre O, so that
or
which is the equation of motion of the pendulum for large oscillation.
(b)
For small amplitude of
oscillation equation (b) reduces to (i.e.
)
from which the natural frequency of the pendulum can be obtained as
rad/sec or
cycle/sec
The time period is given as
sec
Energy method :
In a conservative system (i.e. with no damping) the total energy is constant, and differential
equation of motion can also be established by the principle of conservation of energy.
For the free vibration of undamped system: Energy=(partly kinetic energy + partly
potential energy).
Kinetic energy T is stored in mass by virtue of its velocity.
Potential energy U is stored in the form of strain energy in elastic deformation or work
done in a force field such as gravity, magnetic field etc.
T + U = constant
(2.15)
Hence
where, 1 & 2 represents two instants of time.
Let 1 represents a static equilibrium position (choosing this as the reference point of potential
energy, hereU1=0 ) and 2 represents the position corresponding to maximum displacement of
mass and at this position velocity of mass will be zero and hence T2 = 0. Equation (2.17) reduces
to
T1 + 0 = 0 + U2
(2.18)
If mass is undergoing harmonic motion then T1 & U2 are maximum values.
Tmax = Umax
Our interest is to find natural frequency of the system, writing equation (2.15) for two positions
i.e.
T1 + U1 = T2 + U2 = constant
(2.17)
where, 1 & 2 represents two instants of time.
Let 1 represents a static equilibrium position (choosing this as the reference point of potential
energy, hereU1=0 ) and 2 represents the position corresponding to maximum displacement of
mass and at this position velocity of mass will be zero and hence T2 = 0. Equation (2.17) reduces
to
T1 + 0 = 0 + U2
(2.18)
If mass is undergoing harmonic motion then T1 & U2 are maximum values.
Tmax = Umax
Example 2.2: Obtain equation of motion of a pendulum using energy method.
Solution:
The kinetic and potential energies of the pendulum are given as shown in Figure 2.7
and
(2.19
From the principle of conservation of energy, we have
On substituting energy terms we get
(c)
For pendulum I = ml2, hence equation (c) becomes
Since
can not be zero, hence
Above equation is non-linear because of the term sin
, and it is same as derived in Example 2.1.
Example 2.3 : Obtain equation of motion of a spring mass system using energy method.
Solution: For a spring mass system as shown in Figure 2.2 and Figure 2.8, we have
The loss of potential energy of m due to position x is cancelled by the work done by the
equilibrium force of the spring, (k ) in position x = 0.
On substituting above terms in equation (2.16), we get
or
since
hence
Figure 2.8
For spring mass system, having harmonic motion at the natural frequency, we have
On substituting above terms in equation (2.19), we get
Excercise
2.1:Obtain
the
natural
frequency
of
the
following
systems
(a) A simply supported beam with a central disc as shown in Figure 2.9.
Figure 2.9
Hint:The effective stiffness for the present case can be obtained from the static deflection as
given by
(b)
A
simply
supported
beam
with
offset
disc as
shown
in Figure
2.10.
Figure 2.10
Hint : Effective stiffness can be obtained from the static deflection relations, then natural
frequency is given as
Excercise 2.2:Obtain the natural frequency of a spring-mass system in terms of spring wire
diameter d, coil radius R, number of turns of coil n and modulus of rigidity G of spring
material.
Hint : The static deflection of the mass would be
Excercise
2.3: Obtain
the
torsional
frequency
of
the
system
in Figure 2.11. k1, k2 and k3 are
the
torsional
stiffness
of
segments 1, 2 and 3 respectively. Ip is the polar mass moment of inertia of the disc.
shown
shaft
Figure 2.11
UNIT 3
Damped System
Vibration systems may encounter damping of following types:
1. Internal molecular friction.
2. Sliding friction
3. Fluid resistance
Generally mathematical model of such damping is quite complicated and not suitable for
vibration analysis.
Simplified mathematical model (such as viscous damping or dash-pot) have been developed
which leads to simplified formulation.
A mathematical model of damping in which force is proportional to displacement i.e., Fd = cx is
not possible because with cyclic motion this model will encounter an area of magnitude equal to
zero as shown in
Figure 3.1(a). So dissipation of energy is not possible with this model.
The damping force (non-linearly related with displacement) versus displacement curve will
enclose an area, it is referred as the hysteresis loop (Figure 3.1(b)), that is proportional to the
energy lost per cycle.
(a): Linear relation
(b): Non-linear relation
Figure 3.1: Variation of damping force vs displacement
Viscously damped free vibration :
Viscous damping force is expressed as,
(3.16)
c is the constant of proportionality and it is called damping co-efficient.
Figure 3.2 shows spring-damper-mass system with free body diagram.
From free body diagram, we have
(3.17)
(3.18)
Figure 3.2: Spring-damper-mass system
Let us assume a solution of equation(3.18) of the following form
(3.19)
where s is a constant (can be a complex number) and t is time.
So that
and
, on substituting in equation (3.18), we get,
From the condition that equation (3.19) is a solution for all values of t , above equation gives a
characteristic equation (Frequency equation) as
(3.20)
Equation (3.20) has the following form
solution of which is given as
Solution of equation (3.20) can be written as
(3.21)
Hence the general solution of equation (3.18) from equations (3.19) and (3.21) is given by the
equation
(3.22)
where A and B are integration constants to be determined from initial conditions.
Substituting equation (3.21) into equation (3.22).
(3.23)
The term outside the bracket in RHS is an exponentially decaying function. The term
can have three cases.
(i)
: exponents in equation (3.23) will be real numbers.
No oscillation is possible as shown in Figure 3.3.
This is an overdamped system (Figure 3.3).
Figure 3.3: Overdamped system
(ii)
: exponents in equation (3.23) are imaginary numbers :
we can write
Hence the equation (3.23) takes the following form
Let
and
, equation (3.23) can be written as
(3.24)
where
(iii) Critical case between oscillatory and non-oscillatory motion :
Damping corresponding to this case is called critical damping, cc
(3.25)
Any damping can be expressed in terms of the critical damping by a non-dimensional number
called the damping ratio
(3.26)
Response corresponding to the critical damping case is shown in Figure 3.4 for various initial
conditions.
Figure 3.4: Critical damping
Equation of motion for damped system can be expressed in terms of
and
as
(3.27)
This form of equation is useful in identification of natural frequency and damping of system.
It is useful in modal summation of MDOF system also.
The roots of characteristic equation (3.20) can be written as
(3.28)
with
Depending upon value of damping ratio we can have the following cases
, overdamped condition (Figure 3.3)
, underdamped condition (Figure 3.7)
, critical damping (Figure 3.4)
, undamped system (Figure 3.8)
Equation (3.28) is shown in complex plane Figure 3.5. On the Figure 3.5 various points are described as
follows.
,
for
,
for
s1 and s2 are complex conjugate points on a circular arc,
,
Figure 3.5: Frequency equation in complex plane
In Figure 3.5 various points are as follows
At A and B,
: undamped
Between A and E and between B and E : underdamped
At E,
: critical damping
Between E to F and E to G,
: overdamped
(1) Oscillatory motion : [
, underdamped case]
General solution equation (3.19) becomes:
(3.29)
(3.30)
(3.31)
where
and
where C & D and X,
and
,
are arbitrary constants to be determined from initial conditions, x (0) and
From equation (3.30), we have
On application of initial conditions, we get
x(0)=C
and
; which gives
Hence, equation (3.30), becomes
(3.32)
Equation (3.32) indicates that the frequency of damped system is equal to,
(3.33)
It should be noted that for small
( which is the case of most engineering systems)
(2) Non-oscillatory motion : (over damped case)
(0).
Two roots remain real with one increases and another decreases.
The general solution becomes
(3.34)
so that
On application of initial conditions, we have
x(0)=A + B
and
or
which gives
and
(3) Critically damped systems :
We obtained two roots
Two terms in solution combines to give one constant
From equation (3.32) for critically damped case (when
), we have
(3.35)
Hence the general solution will be
(3.36)
so that,
On application of initial conditions, we get
x(0)=A
and
The necessary and sufficient conditions for crossing once can be obtained as
(3.37)
or
is a necessary condition for crossing time axis once but sufficient conditions is given
by equation (3.37)as shown in Figure 3.4.
Logarithmic Decrement :
Rate of decay of free vibration is a measure of damping present in a system. Greater is the decay,
larger will be the damping.
Damped (free) vibration, general equation of the response is given as
Defining a term logarithmic decrement which is defined as the natural logarithm of the ratio of
any two successive amplitudes as shown Figure 3.6.
since
Td = damped period,
where
We have damped period
= damped natural frequency
, we get logarithmic decrement as
(3.38)
Since
, the above equation reduces to
(3.39)
Experimental determination of natural frequency and damping ratio :
rad/sec, Td can be obtained from displacement-time free vibration oscillations.
, where x1and x2 are two consecute amplitudes in the free vibration displacementtime curve.
Figure 3.6
he above illustration shows for two successive amplitude. But in case, the amplitude are recorded
after "n" cycles, the formula is modified as
Taking log,
Example 3.1: A flywheel of weight 311.36 N is supported on a knife edge at distance 15.24 cm
from its geometric centre. If the measure period of oscillation was 1.22 sec, determine the mass
moment of inertia of the flywheel about its geometric centre.
(1) The flywheel can be considered as a compound pendulum. For a compound pendulum the
period is given by
T = Time period = 1.22 sec.
l = the distance between centers of rotation and gravity = 0.1524 m
g = acceleration due to 9.81 m/sec2
c = the distance between centers of gravity and percussion =
= 0.3698-0.1524 = 0.2174 m
Flywheel weight = 311.36 N
The mass moment of inertia of the flywheel about its geometric centre is given as
O - centre of gravity (or geometric centre)
C - centre of rotation or pivot
Figure 3.7 : A flywheel pivoted on a knife edge
Example 3.2: Determine the natural frequency of the system shown in Figure 3.9 where J is the
mass moment of inertia of the flywheel, r1 and r2 are respectively the inner and outer rim radius
of the flywheel, m is the mass suspended by a thread and k is the stiffness on the spring.
Figure 3.9
Solution: From Figure 3.9 it can be seen that the position of mass m is given by x and the
position of the flywheel is given by . These two co-ordinates are related as
(a)
Hence the present system is SDOF . The kinetic energy will be there due to the mass of the
block m and the polar mass moment of inertia of the flywheel J and it is given as
(b)
On eliminating
in equation (b) from equation (a), we get
(c)
The potential energy is given as
{ No gravity effect since static equilibrium position is chosen as reference axis.}
From Figure 3.9, we have
Hence the potential energy can be written as
(d)
For the conservative system, we have
T + U = Constant
(e)
=Constant
Differentiating equation (e) with respect to time and equating to zero i.e.
or
or
or
(f) For simple
harmonic motion, on comparing with equation (f) we get
Excercise 3.1: A certain system has stiffness 10 Nm-1 and is very heavily damped. The mass is
observed to be moving to the left at 10 mm/sec. when its position is 30 mm to the right of its
equilibrium position. Calculate the resisteance. [Ans: 30 kg/sec]
Excercise 3.2: A lightly damped system is set into vibration with initial condition x(0)=0
and
where
. Show that the subsequent motion is given as
is the damped natural frequency and c is the damping factor.
Excercise 3.3: Obtain the natural frequency as a system as shown in Figure 3.10. Consider the
rod as massless.
Figure 3.10
Hint : Obtain the static deflection
of mass m and note that
Steady State Response due to Harmonic Oscillation :
Consider a spring-mass-damper system as shown in figure 4.1. The equation of motion of this
system subjected to a harmonic force
can be given by
(4.1)
where, m , k and c are the mass, spring stiffness and damping coefficient of the system, F is the
amplitude of the force, w is the excitation frequency or driving frequency.
Figure 4.1 Harmonically excited system
Figure 4.2: Force polygon
The steady state response of the system can be determined by solving equation(4.1) in many
different ways. Here a simpler graphical method is used which will give physical understanding
to this dynamic problem. From solution of differential equations it is known that the steady state
solution (particular integral) will be of the form
(4.2)
As each term of equation (4.1) represents a forcing term viz., first, second and third terms,
represent the inertia force, spring force, and the damping forces. The term in the right hand side
of equation(4.1) is the applied force. One may draw a close polygon as shown in figure 4.2
considering the equilibrium of the system under the action of these forces. Considering a
reference line these forces can be presented as follows.
Spring force =
(This force will make an angle
reference line, represented by line OA).
Damping force =
force, represented by line AB).
Inertia force =
(this force is perpendicular to the damping
force and is in opposite direction with the spring force and is represented by line BC) .
with the
(This force will be perpendicular to the spring
Applied force =
which can be drawn at an angle
reference line and is represented by line OC.
with respect to the
From equation (1), the resultant of the spring force, damping force and the inertia force will be the applied force,
which is clearly shown in figure 4.2.
It may be noted that till now, we don't know about the magnitude of X and which can be easily computed from
Figure 2. Drawing a line CD parallel to AB, from the triangle OCD of Figure 2,
(4.3)
From the previous module of free-vibration it may be
recalled that
Natural frequency
Critical damping
Damping factor or damping ratio
Hence,
(4.5)
or
(4.6)
As the ratio
is the static deflection
amplitude ratio of the system
of the spring,
is known as the magnification factor or
Figure 4.3 shows the magnification factor
frequency ratio and phase angle
frequency ratio plot.
Following observation can be made from these plots.
For undamped system ( i.e.
external excitation equals natural frequency of the system
.
But for underdamped systems the maximum amplitude of excitation has a definite value and it occurs at a
frequency
For frequency of external excitation very less than the natural frequency of the system, with increase in
) the magnification factor tends to infinity when the frequency of
frequency ratio, the dynamic deflection ( X ) dominates the static deflection
factor increases till it reaches a maximum value at resonant frequency
, the magnification
.
For
One may observe that with increase in damping ratio, the resonant response amplitude decreases.
Irrespective of value of
For
For,
, phase angle approaches
for very low value of .
From phase angle frequency ratio plot it is clear that, for very low value of frequency ratio, phase angle
, the magnification factor decreases and for very high value of frequency ratio ( say
, phase angle
, at
, the phase angle
)
.
.
tends to zero and at resonant frequency, it is
and for very high value of frequency ratio it is
.
Figure 4.3 : (a) Magnification factor ~ frequency ratio for different values of damping ratio.
Figure 4.3 : (b) Phase angle ~frequency ratio for different values of damping ratio.
For a underdamped system the total response of the system which is the combination of transient response and
steady state response can be given by
The parameter
will depend on the initial conditions.
It may be noted that as
, the first part of equation (6) tends to zero and second part remains.
Rotating Unbalance
One may find many rotating systems in industrial applications. The unbalanced force in such a system can be
represented by a mass m with eccentricity e , which is rotating with angular velocity as shown in Figure 4.1.
Figure 4.1 : Vibrating system with rotating unbalance
Figure 4.2. Freebody diagram of the system
Let x be the displacement of the nonrotating mass (M-m) from the static equilibrium position, then the
displacement of the rotating mass m is
From the freebody diagram of the system shown in figure 4.2, the equation of motion is
(4.1)
or
This equation is same as equation (1) where F is replaced by
figure 4.3
(4.2)
. So from the force polygon as shown in
(4.3)
or
(4.4)
or
(4.5)
Figure 4.3: Force polygon
or
(4.6)
and
(4.7)
So the complete solution becomes
(4.8)
Figure 4.4 :
plot for system with rotating unbalance
Figure 4.5 : Phase angle ~ frequency ratio plot for system with rotating unbalance
From figure 4.4 and 4.5, following observations may be made for a rotating unbalanced system.
For very low value of frequency ratio (say
) ), the response of the system is very small.
For frequency ratio between 0.5 and1, there is a sharp increase in system response with increase in
frequency of excitation of the system.
At frequency ratio equal to 1, the phase angle is 900.
Maximum response amplitude occurs at a frequency slightly greater than
With increase in damping, the response of the system decreases.
For higher value of
1800
(say >2), the response amplitude approaches
.
and phase angle approaches
Whirling of shaft :
Whirling is defined as the rotation of the plane made by the bent shaft and the line of the centre of the bearing. It
occurs due to a number of factors, some of which may include (i) eccentricity, (ii) unbalanced mass, (iii)
gyroscopic forces, (iv) fluid friction in bearing, viscous damping.
Figure 4.6: Whirling of sh
Consider a shaft AB on which a disc is mounted at S . G is the mass center of the disc, which is at a distance e
from S. As the mass center of the disc is not on the shaft center, when the shaft rotates, it will be subjected to a
centrifugal force. This force will try to bend the shaft. Now the neutral axis of the shaft, which is represented by
line ASB, is different from the line joining the bearing centers AOB. The rotation of the plane containing the line
joining bearing centers and the bend shaft (in this case it is AOBSA) is called the whirling of the shaft.
Considering unit vectors i , j , k as shown in the figure 4.6(b), the acceleration of point G can be given by
(4.9)
Assuming a viscous damping acting at S. The equation of motion in radial direction
(4.10)
(4.11)
(4.12)
(4.13)
Considering the synchronous whirl case, i.e.
(4.15)
where
Taking
is the phase angle between e and r .
, from equation (4.12)
(4.14)
and
(4.15)
Hence,
(4.16)
as
and
From equation (15),
(4.18)
Substituting equation (4.18) in equation (4.15) yields
(4.19)
or
(4.20)
(4.21)
(4.22)
The eccentricity line e = SG leads the displacement line r = OS by phase angle
of damping and the rotation speed ratio
which depends on the amount
When the rotational speed equals to the natural frequency or critical
speed, the amplitude is restrained by damping only. From equation (22) at very high speed
,
and the center of mass G tends to approach the fixed point O and the shaft center S rotates about it in a circle of
radius e.
Support Motion
Many machine components or instruments are subjected to forces from the support. For example while moving in
a vehicle, the ground undulation will cause vibration, which will be transmitted, to the passenger. Such a system
can be modelled by a spring-mass damper system as shown in figure 10. Here the support motion is considered in
the form of
, which is transmitted to mass m , by spring (stiffness k) and damper (damping
coefficient c). Let x be the vibration of mass about its equilibrium position.
Figure 1: A system subjected to support motion
Figure 2: Freebody diagram
Now to derive the equation of motion, from the freebody diagram of the mass as shown figure 2
(1)
let z = x-y
(2)
(3)
(4)
As equation (4) is similar to equation (1) of lecture 1, solution of equation (4) can be written as
(5)
and
If the absolute motion x of the mass is required, we can solve for x = z + y. Using the exponential form of
harmonic motion
(6)
(7)
(8)
(9)
Substituting equation (9) in (1) one obtains
(10)
(11)
(12)
(13)
(14)
The steady state amplitude and Phase from this equation are
(15)
(16)
(17)
Figure 3: Amplitude ratio ~ frequency ratio plot for system with support motion
Figure 4: Phase angle ~ frequency ratio plot for system with support motion
From figure 4.3, it is clear that when the frequency of support motion nearly equal to the natural frequency of the system,
resonance occurs in the system. This resonant amplitude decreases with increase in damping ratio for
. At
, irrespective of damping factor, the mass vibrate with an amplitude equal to that of the support and for
, amplitude ratio becomes less than 1, indicating that the mass will vibrate with an amplitude less than the
support motion. But with increase in damping, in this case, the amplitude of vibration of the mass will increase. So in order
to reduce the vibration of the mass, one should operate the system at a frequency very much greater than
natural frequency of the system. This is the principle of vibration isolation.
times the
Vibration Isolation :
In many industrial applications, one may find the vibrating machine transmit forces to ground which in turn
vibrate the neighbouring machines. So in that contest it is necessary to calculate how much force is transmitted to
ground from the machine or from the ground to the machine.
Figure 4.5 : A vibrating system
Figure 4.5 shows a system subjected to a force
and vibrating with
.
This force will be transmitted to the ground only by the spring and damper.
Force transmitted to the ground
(18)
It is known that for a disturbing force
, the amplitude of resulting oscillation
(19)
Substituting equation (4.19) in (4.18) and defining the transmissibility TR as the ratio of the force transmitted
Force to the disturbing force one obtains
(4.20)
Comparing equation (4.20) with equation (4.17) for support motion, it can be noted that
(4.21)
When damping is negligible
(4.22)
to be used always greater than
Replacing
(4.23)
To reduce the amplitude X of the isolated mass m without changing TR, m is often mounted on a large mass M.
The stiffness K must then be increased to keep ratio K/(m+M) constant. The amplitude X is, however reduced,
because K appears in the denominator of the expression
(4.24)
Figure 6: Transmissibility ~frequency ratio plot
Figure 4.14 shows the variation transmissibility with frequency ratio and it can be noted that vibration will be isolated when
the system operates at a frequency ratio higher than
Equivalent Viscous Damping :
In the previous sections, it is assumed that the energy dissipation takes place due to viscous type of damping
where the damping force is proportional to velocity. But there are systems where the damping takes place in
many other ways. For example, one may take surface to surface contact in vibrating systems and take Coulomb
friction into account. Also in many cases energy is dissipated in joints also, which is a form of structural
damping. In these cases one may still use the derived equations by considering an equivalent viscous damping.
This can be achieved by equating the energy dissipated in the original and the equivalent system.
The primary influence of damping on the oscillatory systems is that of limiting the amplitude at resonance.
Damping has little influence on the response in the frequency regions away from resonance. In case of viscous
damping, the amplitude at resonance is
(4.25)
For other type of damping, no such simple expression exists. It is possible to however, to approximate the
resonant amplitude by substituting an equivalent damping Ceq in the foregoing equation. The equivalent damping
Ceq is found by equating the energy dissipated by the viscous damping to that of the nonviscous damping with
assumed harmonic motion.
(4.26)
Where
must be evaluated from the particular type of damping.
Structural Damping :
When materials are cyclically stressed, energy is dissipated internally within the material itself. Experiments by
several investigators indicate that for most structural metals such as steel and aluminum, the energy dissipated per
cycle is independent of the frequency over a wide frequency range and proportional to the square of the
amplitude of vibration. Internal damping fitting this classification is called solid damping or structural damping.
With the energy dissipation per cycle proportional to the square of the vibration amplitude, the loss coefficient is
a constant and the shape of the hysteresis curve remains unchanged with amplitude and independent of the strain
rate. Energy dissipated by structural damping can be written as
(4.27)
Where
is a constant with units of force displacement.
By the concept of equivalent viscous damping
or
(4.27)
Coulomb Damping :
Coulomb damping is mechanical damping that absorbs energy by sliding friction, as opposed to viscous damping,
which absorbs energy in fluid, or viscous, friction. Sliding friction is a constant value regardless of displacement
or velocity. Damping of large complex structures with non-welded joints, such as airplane wings, exhibit
coulomb damping.
Work done per cycle by the Coulomb force
(4.29)
For calculating equivalent viscous damping
(4.30)
From the above equation equivalent viscous damping is found
(4.31)
Summary
Some important features of steady state response for harmonically excited systems are as follows
The steady state response is always of the form
. Where it is having same frequency
as of forcing. X is amplitude of the response, which is strongly dependent on the frequency of excitation,
and on the properties of the spring—mass system.
There is a phase lag between the forcing and the system response, which depends on the frequency of
excitation and the properties of the spring-mass system.
The steady state response of a forced, damped, spring mass system is independent of initial conditions.
In this chapter response due to rotating unbalance, support motion, whirling of shaft and equivalent damping are
also discussed.