* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Trapezoid Notes File - Northwest ISD Moodle
Rotation formalisms in three dimensions wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
History of trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
Integer triangle wikipedia , lookup
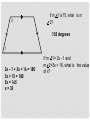
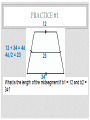
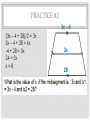
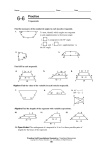
UNIT 7 LESSON 15-2 TRAPEZOIDS MULTIPLE MIDSEGMENTS • Properties of multiple midsegments: 4 congruent Triangles formed Sides of small triangle are ½ of the 1 small Area of original triangle is similar to a large small triangle is ¼ the original Define a trapezoid Draw trapezoid EFGH with FG // EH and right angle at G. G H F E What do the interior angles of a trapezoid add up to? 360 degrees Isosceles trapezoid- A trapezoid with at least congruent sides. two ________ 2 1 congruent Base angles are _____________ Same-Side Interior Angles, supplementary Angles 1 and 2 are _________________________________________ 360 degrees All angles add up to _____________ 2 If m 1 is 75, what is m 2? 105 degrees 1 2x – 1 + 3x + 16 = 180 5x + 15 = 180 5x = 165 x = 33 If m 1= 2x - 1 and m 2=3x + 16, what is the value of x? R S U T congruent Diagonals are ___________ If RT = 5x - 11 and US = 6x - 34, what is the value of x? 5x – 11 = 6x – 34 -11 = x – 34 23 = x MIDSEGMENTS IN TRAPEZOIDS average PRACTICE #1 12 12 + 34 = 46 46/2 = 23 23 34 PRACTICE #2 3x - 4 (3x – 4 + 28)/2 = 3x 3x – 4 + 28 = 6x -4 + 28 = 3x 24 = 3x x=8 3x 28