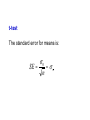* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download t-test
Psychometrics wikipedia , lookup
History of statistics wikipedia , lookup
Foundations of statistics wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Degrees of freedom (statistics) wikipedia , lookup
Taylor's law wikipedia , lookup
Analysis of variance wikipedia , lookup
Misuse of statistics wikipedia , lookup
Practical Statistics Mean Comparisons There are six statistics that will answer 90% of all questions! 1. 2. 3. 4. 5. 6. Descriptive Chi-square Z-tests Comparison of Means Correlation Regression t-test and ANOVA are for the means of interval and ratio scales These are very common statistics…. William S. Gosset 1876-1937 Published under the name: Student t-test come in three types: 1. A sample mean against a hypothesis. t-test come in three types: 1. A sample mean against a hypothesis. 2. Two sample means compared to each other. t-test come in three types: 1. A sample mean against a hypothesis. 2. Two sample means compared to each other. 3. Two means within the same sample. t-test The standard error for means is: SE 0 n x t-test Hence for one mean compared to a hypothesis: t x H0 0 n Each t value comes with a certain degree of freedom df = n - 1 t-test IQ has a mean of 100 and a standard deviation of 15. Suppose a group of immigrants came into London. A random sample of 400 of these Immigrants found an average IQ of 98. Does this group have an IQ below the population average? t-test The test statistic looks like this: 98 100 2 t 2.67 15 0.75 400 There are n – 1 = 399 degrees of freedom. The results are printed out by a computer or looked up on a t-test table. The critical value for 399 degrees of freedom is about 1.97. Of course, we could look this up on the internet…. http://www.danielsoper.com/statcalc/calc08.aspx For the IQ test: t(399) = 2.67, p = 0.00395 t-test Since the test was “one-tailed,” the critical value of t would be -1.65. Therefore, t(399) = -2.67 would indicate that the immigrants IQ is below normal. t-test come in three types: 1. A sample mean against a hypothesis. 2. Two sample means compared to each other. 3. Two means within the same sample. t-test The standard error of the difference between two means looks like this: SE 1 2 n1 n2 2 1 2 2 t-test Therefore the test statistic would look like this: t ( x1 x2 ) ( 1 2 ) 12 n1 22 n2 With degrees of freedom = n(1) + n(2) - 2 t-test Usually this is simplified by looking at the difference between two samples; so that: t ( x1 x2 ) 1 2 1 sp ( ) n1 n2 Where: (n1 1) S (n2 1) S S n1 n2 2 2 p 2 1 2 2 Suppose that a new product was test marketed in the United States and in Japan. The company hypothesizes that customers in both countries would consume the product at the same rate. A sample of 500 in the U.S. used an average of 200 kilograms a year (sd = 20), while a sample of 400 in Japan used an average of 180 kilograms a year (sd = 25). Test the hypothesize….. H0 1 2 0 The test would start be computing: (500 1)20 (400 1)25 2 S 2 p = 500 500 400 2 2 (200 180) t 0.89 500 The results would be written as: (t(898) = 0.89, ns), and the conclusion is that there is no difference in the consumption rate between the U.S. and Japanese customers. (200 180) t 0.89 500 But this is wrong! Can you see why? It is caused by a common mistake of confusing the sampling distribution with a the sample distribution. (200 180) t 1 1 (500)( ) 500 400 The results are written as: (t(898) = 13.33, p < .0001), and the conclusion is that there is a large difference in the consumption rate between the U.S. and Japanese customers. t-test come in three types: 1. A sample mean against a hypothesis. 2. Two sample means compared to each other. 3. Two means within the same sample. t-test come in three types: 3. Two means within the same sample. This t-test is used with correlated samples and/or when the same person or object is measured twice in the same sample. Student T1 T2 d Tom Jan Jason Halley Bill 89 88 87 90 75 90 91 86 90 79 1 3 -1 0 4 The measurement of interest is d. H0 : Average of d = 0 That is… the average difference between test 1 and test 2 is zero. t-test The sampling error for this t-test is: SE 2 D S SD n Were d = score(2) – score(1) t-test The t-test is: D t SD The degrees of freedom = n - 1 Examples can be found at these sites: http://en.wikipedia.org/wiki/T-test http://canhelpyou.com/statistics/tTestDependentSamples.html Suppose there are more than two groups that need to be compared. The t-test cannot be utilized for two reason. 1. The number of pairs becomes large. Suppose there are more than two groups that need to be compared. The t-test cannot be utilized for two reason. 1. The number of pairs becomes large. 2. The probability of t is no longer accurate. Hence a new statistic is needed: The F-test Or Analysis of Variance (ANOVA) R.A. Fisher 1880-1962 The F-test Compares the means of two or more groups by comparing the variance between groups with the variance that exists within groups. F is the ratio of variance: 2 1 2 2 S S http://controls.engin.umich.edu/wiki/index.php/Factor_analysis_and_ANOVA The F-test http://www.statsoft.com/textbook/distribution-tables/ The F-test The probability distribution is dependent upon the degrees of freedom between and the degrees of freedom within. The F-test Typical output looks like this: In SPSS ANOVA looks like this: Descriptives overall N 1.00 2.00 3.00 4.00 Total 64 24 38 6 132 Mean 8.5781 8.2917 9.1053 8.0000 8.6515 Std. Deviation 1.83272 1.60106 .92384 1.09545 1.56773 Std. Error .22909 .32682 .14987 2 .44721S1 2 .13645S 2 95% Confidence Interval for Mean Lower Bound Upper Bound 8.1203 9.0359 7.6156 8.9677 8.8016 9.4089 6.8504 9.1496 8.3816 8.9215 Minimum 1.00 3.00 7.00 7.00 1.00 Maximum 10.00 10.00 10.00 10.00 10.00 ANOVA overall Between Groups W ithin Groups Total Sum of Squares 13.823 308.147 321.970 df 3 128 131 Mean Square 4.608 2.407 F 1.914 Sig. .131 Service Encounter The average age of Iowans over 18 is approximately 47. Is the sample a cross-section of this population by age? A sample mean against a hypothesis. Service Encounter Is the measure of personality different between men and women? Two sample means compared to each other. Service Encounter Is the measure of personality different between men and women? Two sample means compared to each other. Service Encounter Is the measure of personality different between men and women? Service Encounter Do respondents like themselves better than the service provider? Two means within the same sample. Service Encounter Do respondents like themselves better than the service provider? Two means within the same sample. Service Encounter Is the measure of personality different between shopping times? Service Encounter Is personality difference by perception of service encounter? More than two sample means compared to each other. Service Encounter Is personality difference by perception of service encounter? More than two sample means compared to each other.