Download 4.2 Digital Transmission

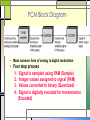
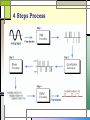
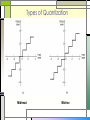
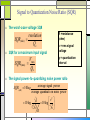
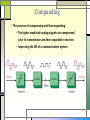
4.2 Digital Transmission
Outlines
□
□
□
□
Pulse Modulation (Part 2.1)
Pulse Code Modulation (Part 2.2)
Delta Modulation (Part 2.3)
Line Codes (Part 2.4)
□
□
□
□
□
Basic scheme of PCM system
Quantization
Quantization Error
Companding
Block diagram & function of TDM-PCM
communication system
Basic scheme of PCM system
□ The most common technique for using
digital signals to encode analog data is
PCM.
□ Example: To transfer analog voice signals
off a local loop to digital end office within
the phone system, one uses a codec.
Cont’d...
□ Because voice data limited to frequencies
below 4000 Hz, a codec makes 8000
samples/sec. (i.e., 125 microsecond/sample).
□ If a signal is sampled at regular intervals at a
rate higher than twice the highest signal
frequency, the samples contain all the
information of the original signal.
PCM Block Diagram
• Most common form of analog to digital modulation
• Four step process
1. Signal is sampled using PAM (Sample)
2. Integer values assigned to signal (PAM)
3. Values converted to binary (Quantized)
4. Signal is digitally encoded for transmission
(Encoded)
4 Steps Process
Cont’d…
□ Analog signal is sampled.
□ Converted to discrete-time continuous-amplitude signal
(Pulse Amplitude Modulation)
□ Pulses are quantized and assigned a digital value.
□ A 7-bit sample allows 128 quantizing levels.
□ PCM uses non-linear encoding, i.e., amplitude spacing of levels is nonlinear
□ There is a greater number of quantizing steps for low amplitude
□ This reduces overall signal distortion.
□ This introduces quantizing error (or noise).
□ PCM pulses are then encoded into a digital bit stream.
□ 8000 samples/sec x 7 bits/sample = 56 Kbps for a single voice channel.
PCM Example
Quantization
□ A process of converting an infinite number of possibilities to a
finite number of conditions (rounding off the amplitudes of
flat-top samples to a manageable number of levels).
Cont’d...
Analog input signal
Sample pulse
PAM signal
PCM code
Cont’d…
 The quantization interval @ quantum
= the magnitude difference between adjacent steps.
 The resolution = the magnitude of a quantum
= the voltage of the minimum step size.
 The quantization error = the quantization noise
= ½ quantum
= (orig. sample voltage – quantize level)
 PCM code = (sample voltage/resolution)
QUANTIZATION ERROR
□ A difference between the exact value of the
analog signal & the nearest quantization level.
Types of Quantization
Midtread
Midrise
Types of Quantizer
1. Uniform type : The levels of the quantized amplitude are uniformly spaced.
2. Non-uniform type : The levels are not uniform.
Dynamic Range (DR)
□ Largest possible magnitude/smallest possible magnitude.
Vmax
Vmax
DR 

Vmin resolution
DR  2n  1
DR (dB)  20 log( DR )
□ Where
□
□
□
□
DR = absolute value of dynamic range
Vmax = the maximum voltage magnitude
Vmin = the quantum value (resolution)
n = number of bits in the PCM code
Example 1
1. Calculate the dynamic range for a
linear PCM system using 16-bit
quantizing.
2. Calculate the number of bits in PCM
code if the DR = 192.6 dB
Coding Efficiency
□ A numerical indication of how
efficiently a PCM code is utilized.
□ The ratio of the minimum number of
bits required to achieve a certain
dynamic range to the actual number
of PCM bits used.
Coding Efficiency = Minimum number of bits x 100
Actual number of bits
Signal to Quantization Noise Ratio (SQR)
□ The worst-case voltage SQR
SQR(min)
resolution

Qe
□ SQR for a maximum input signal
SQR(max)
R =resistance
(ohm)
v = rms signal
voltage
q = quantization
interval
Vmax

Qe
□ The signal power-to-quantizing noise power ratio
average signal power
SQR( dB)  10 log
average quantizati on noise power
 10 log
v2
R
2
( q 12)
R
 v2 
 10 log  q 2 
 12 
Example 2
1.
2.
Calculate the SQR (dB) if the input signal = 2 Vrms
and the quantization noise magnitudes = 0.02 V.
Determine the voltage of the input signals if the
SQR = 36.82 dB and q =0.2 V.
Effect of Non-Linear Coding
Nonlinear Encoding
□ Quantization levels not evenly spaced
□ Reduces overall signal distortion
□ Can also be done by companding
Companding
• The process of compressing and then expanding.
• The higher amplitude analog signals are compressed
prior to transmission and then expanded in receiver.
• Improving the DR of a communication system.
Companding Functions
Method of Companding
□ For the compression, two laws are adopted: the -law in US
and Japan and the A-law in Europe.
□ -law
□
Vout 
□ A-law
Vout
Vmax ln( 1   Vin Vmax )
ln( 1   )

A Vin Vmax
 Vmax
1  ln A


Vin
1

ln(
A
Vmax )

 1  ln A
Vin 1
0

Vout A
1 Vin

1
A Vout
Vmax= Max uncompressed
analog input voltage
Vin= amplitude of the input
signal at a particular of
instant time
Vout= compressed output
amplitude
A, = parameter define the
amount of compression
□ The typical values used in practice are: =255 and A=87.6.
□ After quantization the different quantized levels have to be
represented in a form suitable for transmission. This is done via
an encoding process.
Example 3
□ A companding system with µ = 255
used to compand from 0V to 15 V
sinusoid signal. Draw the characteristic
of the typical system.
□ Draw an 8 level non-uniform quantizer
characteristic that corresponds to the
mentioned µ.
Cont’d...
μ-law
A-law
PCM Line Speed
□ The data rate at which serial PCM bits are clocked out of the
PCM encoder onto the transmission line.
samples
bits
line speed 
X
second sample
□ Where
□ Line speed = the transmission rate in bits per second
□ Sample/second = sample rate, fs
□ Bits/sample = no of bits in the compressed PCM code
Example 4
□ For a single PCM system with a sample
rate fs = 6000 samples per second and
a 7 bits compressed PCM code,
calculate the line speed.
Virtues & Limitation of PCM
The most important advantages of PCM are:
□ Robustness to channel noise and
interference.
□ Efficient regeneration of the coded signal
along the channel path.
□ Efficient exchange between BT and SNR.
□ Uniform format for different kind of baseband signals.
□ Flexible TDM.
Cont’d…
□ Secure communication through the use of
special modulation schemes of encryption.
□ These advantages are obtained at the cost of
more complexity and increased BT.
□ With cost-effective implementations, the cost
issue no longer a problem of concern.
□ With the availability of wide-band
communication channels and the use of
sophisticated data compression techniques, the
large bandwidth is not a serious problem.
Time-Division Multiplexing
□ This technique combines time-domain
samples from different message signals
(sampled at the same rate) and transmits
them together across the same channel.
□ The multiplexing is performed using a
commutator (switch). At the receiver a
decommutator (switch) is used in
synchronism with the commutator to
demultiplex the data.
Cont’d…
□ TDM system is very sensitive to symbol dispersion,
that is, to variation of amplitude with frequency or
lack of proportionality of phase with frequency. This
problem may be solved through equalization of
both magnitude and phase.
□ One of the methods used to synchronize the
operations of multiplexing and demultiplexing is to
organize the multiplexed stream of data as frames
with a special pattern. The pattern is known to the
receiver and can be detected very easily.
Block diagram of TDM-PCM communication
system
END OF PART 2.2