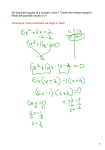Download Multiplying and Factoring Polynomials Part I

Multiplying
and Factoring
Polynomials
Part I
Math 100
Ms. Edna Reyes.
22 July 2010
Definition of Polynomials
Expression with:
- a finite number of terms
- with variables and constants
- Using only addition, subtraction, and
multiplication
- If there are exponents these are whole
numbers and non-negative
YES: x2 + 2x + 1
terms
NO: 5y
x
Other Definitions
-
Degree of the variable is the exponent of that
variable
x3 : degree = 3
Degree of the term is the sum of degrees of the
variables
x2y2: degree = 2+2 = 4
Degree of the polynomial is the largest degree of
any term:
X3 + y2 + 1 : degree = 3
Polynomials are usually written in order of descending degrees.
Multiplying Polynomials
• To multiply a monomial (one term) by a
polynomial, use the distributive property
-x3 (9x4 – 2x3 + 7) = -x3(9x4) -x3(–2x3) -x3(7) Use distributive prop.
= -9x3+4 + 2x3+3 -7x3 Multiply coefficients and
add exponents (of same
variable).
= -9x7 + 2x6 -7x3
Simplify.
Example
5n (3n3 – n2 + 8) = 5n(3n3) +5n(–n2) +5n(8) Use distributive prop.
= 15n1+3 – 5n1+2 +40n Multiply coefficients and
add exponents (of same
variable).
= 15n4 - 5n3 + 40n Simplify.
Exercises
1.
2.
3.
4.
5.
6.
7x(x + 4)
(b + 11)2b
3m2(10+m)
-w2(w-15)
4x(2x3 – 7x2 + x)
-8y3(7y2 – 4y -1)
Factoring a Monomial from a
Polynomial
Step 1: To factor out a monomial (one term) by
a polynomial, first look for the Greatest
Common Factor (GCF).
To find GCF: list prime factors of each term.
Identify the factors common to ALL terms.
Finding GCF - Example
5x3 + 25x2 + 45x
5x3 : 5 ·x ·x ·x
25x2 : 5 ·5 ·x ·x
45x: 5 ·3 ·3 ·x
GCF is 5 · x or 5x
Factoring a Monomial from a
Polynomial
Step 2: Factor out the GCF from each term of
the polynomial.
5x3 + 25x2 + 45x = 5x(x2) + 5x(5x) + 5x(9)
= 5x(x2 + 5x + 9)
Example: 4x5 - 24x3 + 8x
Find GCF:
4x5 2 ·2 ·x ·x ·x ·x ·x
24x3 3 ·2 ·2 ·2 ·x ·x ·x
8x: 2 ·2 ·2 ·x
GCF is 4x
4x5 - 24x3 + 8x = 4x(x4) +4x(-6x2) + 4x(2)
= 4x(x4 -6x2 + 2)
Exercises
Find GCF:
1. 12x + 20
2. 8w2 – 18w
3. a3 + 6a2 -11a
4. 4x3 + 12x – 28
5. 14z4 – 42z3 + 21z2
Factor each polynomial:
1. 9x - 6
2. t2 + 8t
3. 14n3 – 35n2 + 28
4. 5k3 + 20k2 – 15
5. g4 + 24g3 + 12g2 + 4g
Pearson p. 483