Download Chapter 22: Inference about a Population Proportion Sampling

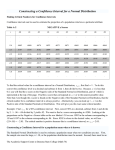
Chapter 22: Inference about a Population Proportion
Sampling distribution of a Sample Mean
Individual observations
N (µ, σ)
The sample mean x of an SRS of size n
σ
N (µ, √ )
n
Sampling distribution of a Sample Proportion
If we draw an SRS of size n from a large population that contains proportion p of successes.
1) Let p̂ be the sample proportion of success,
p̂ =
number of successes in the sample
total number of indeviduals in the sample
2)Sampling distribution of p̂ is the very close value of the population proportion p.
3) The standard deviation of the distribution of p̂ is
√
p(1 − p)
.
n
4) As the sample size increases, the sampling distribution of p̂ becomes
approximately Normal.
√
(
p(1 − p) )
N p,
n
Ex. Medical Malpractice
In a study of 1228 randomly selected medical malpractice lawsuits, it is found that 856 of them
were later dropped or dismissed.
a. What is the best point estimate of the proportion of medical malpractice lawsuits
that are dropped or dismissed?
b. Construct a 99% of confidence interval estimate of the proportion of medical malpractice
lawsuits that are dropped or dismissed?
A point estimate: A single value used to approximate a population parameter.
The sample proportion p̂ is the best point estimate of the population proportion.
It is like that the sample mean x is the best point estimate of the population mean.
A Confidence Interval (CI): A range (or an interval) of values used to estimate
the true value of a population parameter.
The confidence level:
The degree of confidence:
The confidence coefficient: The probability 1 − α that the confidence interval actually
contains the population parameter.
There are three common choices for the confidence level:
90% (α = 0.10)
95% (α = 0.05)
99% (α = 0.01)
Critical z-value:
Critical Values: The number zα/2 is a critical value that is a z score with the property
that it separates an area of α/2 in the right tail of the standard normal
distribution.
Confidence Level
α
Critical Value, E = zα/2
————————————————————————————
90%
0.10
1.645
95%
0.05
1.96
99%
0.01
2.575
Requirements for using formula for the confident interval
for the population proportion
(a) The sample is a simple sample.
(b) The conditions for the binomial distribution are satisfied.
1. The procedure has a fixed number of trials.
2. The trial must be independent.
3. Each trial must all outcomes classified into two categories.
4. The probability of a success remains the same in all trials.
(c) There are at least 15 successes and at least 15 failures.
(We need that np ≥ 10 and nq ≥ 10 are satisfied.)
Estimating a Population Proportion
Estimating a Population Proportion
Margin of Error: The maximum likely difference (with probability 1−α) between the observed
sample proportion p̂ and the true value of the population proportion p.
√
E = z∗ ·
p̂ (1 − p̂)
n
(margin of error)
Confidence Interval for Estimating a Population Proportion p
√
∗
p̂ − z ·
p̂ (1 − p̂)
n
√
∗
< p < p̂ + z ·
p̂ (1 − p̂)
n
Round-Off Rule for Confidence Interval Estimates of p:
Round the confidence interval limits for p to four significant digits.
Interpreting a Confidence Interval:
We are 99% confident that the interval from 0.663 to 0.731 actually does contain the true value
of the population proportion p.
We have 99% confidence to say that the interval from 0.663 to 0.731 actually does contain
the true value of the population proportion p.
Finding the Sample Size
( z ∗ )2
· p̂ · (1 − p̂)
When an estimate p̂ known
m
( z ∗ )2
n=
· 0.25
When no estimate p̂ known
m
n=
Round-Off Rule for Determining Sample Size:
If the computed sample size n is not a whole number, round the value of n up to the next larger
whole number.
Ex. Find the minimum sample size.
Margin of error: 0.005; confidence level : 99%;
p̂ and q̂ unknown.
Ex.
In a survey of 1002 people, 701 said that they voted in a recent presidential election.
Find a 95% confidence interval estimate of the population of people who say that
they voted.
Ex.
In a Gallup poll, 1000 randomly selected adults were surveyed. 29% of them said that
they used the Internet for shopping at least a few times a year. Find the 95% confidence
interval of the true proportion of adults who use the Internet for shopping.
Ex.
When Mendel conducted his famous genetics experiments with peas. One sample of offspring
consisted of 428 green peas and 152 yellow peas. Find a 90% confidence interval estimate
of the percentage (proportion) of yellow peas.
Significance tests for a proportion
Test Statistic Formulas
For proportion:
z=√
p̂ − p0
p0 (1 − p0 )
n
⇒ We are going to use Normal Distribution Table to find P -value.
Ex.
The new sheriff complies records showing that among 30 recent robberies, the arrest
rate is 30%, so she claims that her arrest rate is greater than the 25% rate in past.
Is there sufficient evidence to support her claim that the arrest rate is greater
than 25%? Use a 0.10 significant level.
Ex.
In a study, subjects were asked to taste two wine samples in sequence. Both samples given
to a subject were the same wine, although subjects were expecting to taste two different samples
of a particular variety. Of the 32 subjects in the study, 22 selected the wine presented first,
when presented with two identical wine samples. Do the data give good reason to conclude
that the subjects are not equally likely to choose either of the two positions when presented
with two identical wine samples in sequence?