* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 2.3 Rate of Change
Survey
Document related concepts
Transcript
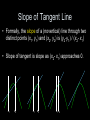
2.3 Rate of Change (Calc I Review) Average Velocity Suppose s(t) is the position of an object at time t, where a ≤ t ≤ b. The average velocity, or average rate of change of s with respect to t, of the object from time a to time b is average velocity = change in position change in time s(b) - s(a) = b-a Change in Time If we define ∆t to be b - a, then b = a + ∆t, and average velocity = s(b) - s(a) b-a = s(a + ∆ t) - s(a) ∆t Limits Suppose that as x approaches some number c, the function f(x) approaches a number L. We say that the limit of f(x) as x approaches c is L, and we write lim f(x) = L x→c Instantaneous Velocity The instantaneous velocity, or the instantaneous rate of change of s with respect to t, at t = a is lim s(a + ∆t) - s(a) ∆t→ 0 ∆t provided that the limit exists Slope of Tangent Line • We can think of decreasing ∆t as zooming in closer on the graph of the function s. • Q.: What happens to the appearance of the function as we do this? Slope of Tangent Line • We can think of decreasing ∆t as zooming in closer on the graph of the function s. • Q.: What happens to the appearance of the function as we do this? • A.: The line appears to straighten out - i.e., we start seeing the linear slope as ∆t approaches zero. Slope of Tangent Line • Formally, the slope of a (novertical) line through two distinct points (x1, y1) and (x2, y2) is (y2-y1) / (x2- x1) • Slope of tangent is slope as (x2- x1) approaches 0. x1 x2 x1 x2 x1x2 Derivative The derivative of y = s(t) with respect to t at t = a is the instantaneous rate of change of s with respect to t at a: s’(a) = lim s(a + ∆t) - s(a) = ∆t→ 0 ∆t dt t = a dy provided that the limit exists. If the derivative of s exists at a, we say the function is diffentiable at a. What would it mean for a function not to be differentiable? s(t) Differentiablity t not continous: s(t) = -1 if t = 0 s(t) = t2 otherwise continuous differentiable: but not differentiable: s(t) = |t| s(t) = t2 Differential Equations • A differential equation is an equation that contains one or more derivatives. • An initial condition is the value of the dependent variable when the independent variable is zero. • A solution to a differential equation is a function that satisfies the equation and initial conditions. Second Derivative • Acceleration is the rate of change of velocity with respect to time. • The second derivative of a function y = s(t) is the derivative of the derivative of y w.r.t. the independent variable t. The notation for this second derivative is s”(t) or d2y/dt2.