Download A Calculation of Electric Field Strengths for Light in a Multilayer Thin

A Calculation of Electric Field Strengths
for Light in a Multilayer Thin Film Structure
by Brent Royuk, Bachelor of Science
An Advanced Research Paper Submitted in Partial
Fulfillment of the Requirements
For the Master of Science Degree
Department of Physics
in the Graduate School
Southern Illinois University at Edwardsville
Edwardsville, IL
July, 1996
Abstract
Equations are derived that give electric field strengths for light incident on a multilayer thin film
structure. The equations assume the structures have semi-infinite incident layers and substrates,
and apply to structures with any number of intermediate layers. All layers are separated by
boundaries that are planar and parallel. The form of the equations is recursive, and no matrices
are used to find the reflectance and transmittance of a multilayer. The equations are used to
generate electric field strength vs. depth plots for a variety of thin film examples that illustrate
some familiar design characteristics.
ii
Table of Contents
ABSTRACT
ii
ACKNOWLEDGMENTS
iv
LIST OF FIGURES
v
Chapter
Page
I.
INTRODUCTION
1
II.
BACKGROUND THEORY
3
Plane Electromagnetic Waves
Optical Constants
Polarization States
Boundary Conditions
Fresnel’s Coefficients
Rouard’s Method
3
4
5
6
7
8
III.
IV.
V.
CALCULATION OF THE ELECTRIC FIELD
10
Notational Conventions
S-Polarized Light
Incident medium
Substrate
Intermediate Phases
P-Polarized Light
Incident medium
Substrate
Intermediate Phases
Tangential Component
Normal Component
Equation Summary
10
11
NUMERICAL ANALYSIS
36
Two Layers on an Absorbing Substrate
Single Layer AR Coating
Dielectric HR Mirror
Critical Angle
Plasmon Resonance Angle
Transmittance Properties of Copper
36
40
44
46
50
54
SUMMARY
56
22
34
REFERENCES
58
iii
Acknowledgments
First and foremost, I wish to thank my thesis advisor, Dr. Arthur Braundmeier. The derivation
that is the heart of this paper follows a roughed-out version that Dr. Braundmeier completed
more than ten years before this paper was written. I will be forever grateful to him for the many
hours of help, advice and encouragement that he has given me, most of it long distance. One of
my best memories from this project is when Dr. Braundmeier and I utilized a ten-hour problem
solving session to remove the glitches from my numerical calculation process.
I would like to thank the members of my thesis committee, Drs. George Henderson and Jerry
Pogatshnik, and I am also indebted to all the fine teachers in the SIUE Physics Department who
taught my classes.
Finally, I thank my dear wife, Sandra, without whom I never could have survived our “three
year plan.” It has been difficult but rewarding to raise two babies and a Master’s Degree
contemporaneously.
Soli Deo Gloria
iv
List of Figures
Figure
Description
2.1
2.2
2.3
3.1
3.2
3.3
3.4
3.5
3.6
4.1
4.2
The total electric field, composed of a transmitted and a reflected part
Labeling angles at the interface between medium j-1 and medium j
S- and p-polarized light
Conventions used to label optical media and interfaces
Notation used for labeling field strengths at interfaces
Geometric relationships for s-polarized light
Finding the direction of the wave vector
The transmitted portion of the electric field at an interface
Geometric relationships for p-polarized light
Diagram of a thin film
Electric field strengths for a thin film consisting of 400 nm Si, 400 nm Al2 O3
on a GaAs Substrate, with light incident at 30o and λ o = 550 nm
Detail of Figure 4.2
Single layer quarter wavelength AR coating: 72 nm layer HfO2 on Si
substrate with light at normal incidence and λ o = 550 nm, R = 0.17%.
Uncoated silicon substrate: R = 36%.
Single layer quarter wavelength AR coating: 72 nm layer HfO2 on Si
substrate with light incident at 30o and λ o = 550 nm. RS = 1.4% and
RP = 0.74%. An uncoated silicon substrate would have reflectances of
RS = 41.0% and RP = 30.6%
Imperfect single-layer AR coating: 150 nm layer HfO2 on Si substrate
with light incident at 30o and λ o = 550 nm. RS = 41.0% and RP = 30.6%.
Schematic of a design for a dielectric HR mirror
A dielectric high reflectance structure: Eight alternating layers of quarter
wavelength layers of TiO2 and MgF2 on glass substrate with light incident
at 30o and λ o = 550 nm. RS = 95.9% and RP = 90.4%.
Reflectance vs. angle for light traveling from glass into air
Electric field strengths for glass to air at 40 o with λ o = 550 nm
Electric field strengths for glass to air at 45 o with λ o = 550 nm
Reflectance vs. incident angle for light traveling from quartz through a
50 nm layer of silver into air with λ o = 550 nm
Electric field strengths for light traveling from quartz through a 50 nm
layer of silver into air at 40o incident angle with λ o = 550 nm
Electric field strengths for light traveling from quartz through a 50 nm
layer of silver into air at 45.3o incident angle with λ o = 550 nm
Electric field strengths for a 50 nm layer of copper on glass at 30o with
λ o = 500 nm
Electric field strengths for a 50 nm layer of copper on glass at 30o with
λ o = 1000 nm
4.3
4.4
4.5
4.6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
Page
v
3
5
6
10
11
12
14
21
22
37
38
39
42
43
44
45
46
47
48
49
51
52
53
54
55
Chapter I
Introduction
The purpose of this paper is to derive equations that allow one to calculate electric field
strengths within a multilayer thin film structure. After the equations have been derived,
calculations will be made to demonstrate their utility in finding electric field strengths for light
incident on several thin film optical stacks.
With the equations in hand, one needs to know a) the strength of the electric field for the light
at the first interface of the incident medium, b) the angle of incidence at the first interface, c)
the thickness of each element of the stack, and d) the optical constants (n and k values) for each
optical element, which are a function of the frequency of the incident light.
It is not difficult to find the electric field strength for light propagating through a single
medium. The most arduous task in this derivation is to keep track of the field strengths as the
light travels across each interface of the thin film stack. The Fresnel coefficients provide a
mathematical description of the electric fields as they cross these interfaces, with separate
treatments being necessary for the p- and s-polarized varieties of light. Furthermore, when
dealing with a multilayer structure, one must take into account all the multiple reflections that
may occur between the layers. This is accomplished through the use of Rouard’s method.
In order to “divide and conquer” the problem of calculating electric field strengths in a thin
film, a separate mathematical treatment is necessary for each of three different regions of the
thin film structure: the incident medium, the intermediate layers, and the substrate. We will
1
assume the incident medium and the substrate to be semi-infinite in extent in order to eliminate
any reflections that would occur from a “front” surface in the incident medium or a “back”
surface in the substrate. Only one equation will be necessary for each of these regions when
considering s-polarized light, while there will need to be two equations in each region for ppolarized light, one for the electric field component tangential to the interface and one for the
normal component. This strategy will yield a total of nine equations that are derived in Chapter
III.
Chapter IV will be occupied with the application of the equations to some common thin-film
structures, showing some electric field strength vs. depth plots. We will investigate several thin
film designs that are chosen to demonstrate some of the more interesting and educational
electric field strength scenarios that occur in thin film structures.
The electric field profile for a thin film structure can be useful to a thin film designer, especially
if the structure is to be used in an environment where the electric field strengths are high, such
as high energy laser applications. High index optical materials are especially susceptible to
electric field damage, since energy density scales as n2 , the square of the refractive index. When
the electric field strength profile is solved for a given structure, the designer can see where in the
stack the field would be especially high. Designs can be altered in order to insure that regions
of high field do not occur at interfaces, since a thin film is most vulnerable at the interfaces,
where different materials adhere to each other. The forces on the charges in the film materials
that are due to the electric field of the incident light can pull the layers apart or produce a
shearing force, which can cause films to disintegrate, de-laminate or crack.
2
Chapter II
Background Theory
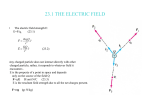
Plane Electromagnetic Waves
In order to describe the electric field for light propagating through any optical element in a thin
film stack, we will use the exponential wave equation, E = Eo e i( k ⋅r −ωt ) , which is a solution of
Maxwell’s equations1 . In all phases of a thin film stack except the semi-infinite substrate, this
field will consist of two parts: a transmitted part and a reflected part. The equation for the total
field in layer j will be written as:
E j = E 0(j t ) e
i( kt j ⋅r −ω t)
)
+ E 0(r
e
j
i(k rj ⋅r −ω t)
.
(2.1)
Ej
)
E 0(t
e
j
i(k tj ⋅r− ω t)
E 0(r)
e
j
i( k rj ⋅r− ω t)
Layer j
Figure 2.1: The total electric field, composed of a transmitted and a reflected part
3
This wave equation is explicitly time-dependent, but in our treatment of the equations the timedependence will tend to become irrelevant since time-averages are calculated by taking the
absolute squares of the measurable quantities, leaving expressions that are constant in time. It
should be noted that in all equations in this paper vectors will be denoted with boldfaced letters
and scalars will be normal type. A caret (^) over a boldfaced variable denotes a unit vector and a
tilde (~) over a variable indicates a complex number.
Optical Constants
The wave vector, kj, can be written as k j =
2π˜n j ˆ
S , where Sˆ j is a unit vector in the direction of
λo j
the wave’s energy propagation2 and λ o is the wavelength of the incident light in vacuum. The
constant n˜ j is the complex index of refraction for the jth layer. It has a real and a complex part:
n˜ j = n j − ik j .3 In the wave equation, nj is the index of refraction and determines the phase of
the wave as it propagates through the medium, while kj is an absorption coefficient that will
cause the wave to “die out” as it propagates through the medium. These constants are
characteristic of the material through which the wave is propagating and the frequency of the
incident wave. Also useful is Snell’s law:
n˜ j sin θ˜ j = n˜ j +1 sin θ˜ j +1 .
(2.2)
Snell’s law can be derived by applying conservation of momentum for light incident at a
boundary4 . This equation gives the refraction angles for the light as it passes into media with
different optical constants. Note that θ˜ is, in general, complex. Figure 2.2 shows light
refracting at a layer boundary with the angles labeled.
4
n˜ j
n˜ j − 1
θ˜ j
θ˜ j −1
Interface j-1
Figure 2.2: Labeling angles at the interface between medium j-1 and medium j
Polarization States
Electromagnetic waves can have two different polarization states, s- and p-polarization. Spolarized waves have their electric field vectors normal to the plane of incidence and are thus
tangential to the interface . P-polarized light consists only of waves that have their electric field
vectors parallel to the plane of incidence. The p-polarized field vectors will therefore have
components tangential to the interface and normal to the interface5 . These two components
require separate treatments in the derivation. Figure 2.3 illustrates the two polarization states.
The small double-headed arrows arranged along the propagation vectors show the direction of
the electric field vectors for the light.
Interfaces
5
Figure 2.3: S- and p-polarized light
Boundary Conditions
In order to obtain a full description of electric field strengths for light propagating through a
medium, one needs to make use of both the electric field, E, and the magnetic field, H. These
are related by6
 ε˜ j 
Hj =  
 µj 
1/2
Sˆ j × E j .
(2.3)
In this equation, ε˜ j is the permittivity of the medium and µ j is the permeability of the medium,
which measure the tendency of the material to allow propagation of electric and magnetic fields,
respectively. These values are related to the complex index of refraction for a given material by
n˜ j = (µ j ε˜ j )
1/2
. The cross product in equation 4.2 shows us that the electric and magnetic
fields are perpendicular to each other. As these fields propagate across an interface, we note
that Maxwell’s equations predict that the tangential portion of the fields must be continuous
across the interface7 . These boundary conditions will be enforced during the derivation and will
have markedly different implications for the treatment of s- and p-polarized light.
6
Fresnel’s Coefficients
As light propagates through an interface into a new medium, we need a way to relate the
amplitudes of the transmitted and reflected portions of the light. We can do this by making use
of Fresnel’s coefficients. We will consider the (j-1) interface to be the interface between the
(j-1)th and the jth media, and will define the Fresnel reflection coefficient for that interface as r˜j − 1.
For the (j-1) interface, the Fresnel reflection coefficient is defined as r˜j − 1 ≡
th
E(jr−1)
t)
E( j−1
. So
considering only reflections that take place at a single interface, the field reflected at that
interface will be related to the incident field by E (rj −1) = r˜j−1 E(jt−1) .
We note that all three quantities in the preceding equation are complex numbers, so r˜j − 1 must
provide information about the phase relationship between the incoming and reflected wave,
along with relating their field strengths8 .
The Fresnel reflection coefficients come in two varieties, one for s-polarized light and one for ppolarized light. We define these as:
r˜j-1S ≡ s-polarized Fresnel reflection coefficient, and
r˜j-1P ≡ p-polarized Fresnel reflection coefficient.
The following equations are derived by conserving the tangential components of the E and Hfields at an interface and are given by9
r˜j-1S =
n˜ j cosθ˜ j − n˜ j − 1 cosθ˜ j −1
and
n˜ j cosθ˜j + n˜ j −1 cosθ˜j − 1
(2.4)
7
r˜j P-1 =
n˜ j cosθ˜ j −1 − n˜ j−1 cosθ˜ j
.
n˜ j cosθ˜ j −1 + n˜ j −1 cosθ˜ j
(2.5)
These coefficients are defined so that there is no phase change difference between s- and ppolarized light that is reflected from an interface at normal incidence. A phase change
difference of
π
is sometimes “built into” the equations when problems of this type are
2
considered. We will not adopt that convention in this paper.
The amplitude of light transmitted across an interface can be described by the Fresnel
transmission coefficients, which are defined by t˜j −1 ≡
10
E(jt )
E(j t−1)
, and are given as
S
t˜j-1
=
2˜n j − 1 cosθ˜ j −1
and
n˜ j cosθ˜j + n˜ j −1 cosθ˜j − 1
(2.6)
t˜jP-1 =
2 n˜ j cosθ˜ j−1
.
n˜ j cosθ˜ j −1 + n˜ j−1 cosθ˜ j
(2.7)
Rouard’s Method
Equations 4.4 - (2.7) apply only to a single interface. When analyzing light that is propagating
through a multilayer optical stack, it is necessary to take into account light that may reflect back
and forth between layer interfaces, thus increasing the effective reflective properties of the stack.
Rouard’s expression sums these multiple reflections and gives a single coefficient that
represents the reflection due to all materials beyond a given interface. This method sums the
multiple bounce contributions as part of an infinite mathematical series that produces the
exponential terms in the equations below. The series is convergent since the more bounces that
occur, the weaker they are. The result is11 :
8
 4πil j n˜ j cosθ˜ j 
r˜j -1 + r˜j′ exp 

λo


r˜j′-1 =
.
 4πil j n˜ j cos θ˜ j 
1+ r˜j′r˜ j-1 exp 

λo


(2.8)
The prime (′) denotes the “total” coefficient that takes into account all multiple reflection
possibilities beyond the interface. We note that equation (2.8) is a recursive relation that
necessitates knowledge of the “total” coefficient at the interface beyond the one in question.
So in practice it is necessary to “work your way back” from the substrate to the incident
medium, finding the total reflection coefficient at each interface in turn. This process will
eventually yield a total combined reflection coefficient for the whole stack, r˜1′ . This constant
will be featured prominently when we derive the equations for the incident medium, where we
don’t care what the light is “doing” inside the thin film, but only need to know its total
reflectance. The total absolute reflectanceof the stack, R, which gives the percentage of energy
2
reflected by the stack, is related to r˜1′ by R = r˜1 ′ .
Instead of following this recursive process, it is also quite common to use matrix notation to
reduce multiple layer contributions to a single total reflection coefficient in matrix form.
The corresponding treatment of the transmission coefficients yields12
 2πil j n˜ j cosθ˜ j 
t˜j′ t˜ j−1 exp 

λo


t˜j′-1 =
.
 4πil j n˜ j cos θ˜ j 
1+ r˜j′r˜ j-1 exp

λo


(2.9)
9
Chapter III
Calculation of the Electric Field
Notational Conventions
As we consider a multilayer thin film system, the following conventions will be used to label the
interfaces and the optical indices for the stacked media:
Incident
Medium
n1
Interface: 1
Substrate
n˜ 2
n˜3
2
n˜4
3
.....
4
n˜ j -1 n˜ j n˜ j +1
j-2 j-1
j
j+1
.....
n˜m −1 n˜m
m-2 m-1
Figure 3.1: Conventions used to label optical media and interfaces
In all diagrams in this paper, the incident medium will be to the left of the substrate, so the
incident light will always travel left to right.
It will often be important for us to refer to the electric field just at the edge of a given medium.
The notation that will be used to label electric field strengths at the edges of interfaces is
summarized in Figure 3.2:
10
nˆ j
nˆ j +1
E (rj- )
Ej(r+ )
E (tj -)
E (j +t )
interface:
j
j+1
Figure 3.2: Notation used for labeling field strengths at interfaces
The superscript “t” or “r” indicates whether the variable represents the transmitted or
reflected electric field. The subscript refers to the interface number, with the raised “+” or “-”
denoting the “outgoing” or “incoming” sides of the interface.
S-Polarized Light
For s-polarized light, we have the following geometry for the incident and reflected fields:
kˆ
ˆi
11
H0
Figure 3.3: Geometric relationships for s-polarized light
INCIDENT MEDIUM
For the incident medium, we assume, necessarily and without loss of generality, that n1 is real.
There is therefore no absorption in the incident medium. The electric field in the incident
medium can then be written as E1 = E10(t ) e i ( k1⋅r −ω t ) + E10( r ) e i( k1⋅ r− ω t ) , where E10( r ) = r˜1′E10( t) . We
t
r
recall that r˜1′ is the total reflection coefficient at the first interface for all layers beyond the first
interface and is calculated with Rouard’s method. We next define R to be the energy reflected
r
from the multilayer stack. We note that R = r˜1′ 2 and the inverse relationship is r˜1′ = R1/2 e iδ ,
where δ r is the phase change that occurs when the light is reflected off the first interface of the
[
]
thin film structure. Thus we can write E1 = E0(1 t ) ei ( k1 ⋅r −ω t ) + R1/2 eiδ ei( k1 ⋅r −ω t ) . This
t
r
r
expression gives E1 as a vector quantity. Since we have assumed the incident medium to be
transparent, E1 is real, which will not generally be true in layers beyond the first interface.
While it is mathematically necessary for the electric field to be a complex vector quantity, we
will ultimately be interested in calculating real measurable field strengths, i.e. the intensity of the
12
light, which can be found by calculating the time-average of the electric field vector. This is
defined as E 2 ≡
1 2
E . The absolute value for a complex quantity is found by taking E⋅E* ,
2
so the time-average will always be real.
The time-average of the electric field in the first medium is
E12 =
2
1
1
E1 = ( E1 ⋅ E1* )
2
2
[
][
]
=
r
r
t
r
r
2
1 i(k t1 ⋅r− ω t )
e
+ R1/2 e iδ ei ( k1 ⋅r− ω t ) e -i( k1 ⋅ r− ω t ) + R1/2 e −iδ e −i ( k1 ⋅r −ω t ) ( E10( t ) )
2
=
r
t
r
r
r
t
1
1+ R + R1/2 e -iδ e i(k1 ⋅ r −k1⋅ r ) + e iδ e i(k1 ⋅r −k1 ⋅r )
2
[
(
)]( E
)
0( t ) 2
1
We can simplify the exponential terms if we let Φ = k1t ⋅ r − k1r ⋅ r −δ r , so
E12 =
[
]
2
1
1 + R + R1/2 (e iΦ + e-iΦ ) ( E10(t ) ) .
2
But e iΦ + e- iΦ = 2cos Φ , so
2
1
E12 =  (1+ R ) + R1/2 cosΦ ( E10( t) )
2

2
1
=  (1 + R ) + R1/2 cos ( k t1 ⋅ r − k 1r ⋅ r −δ r )( E10( t) ) .
2

The cosine is an even function, i.e. cosΦ = cos (−Φ ) , so we can rewrite the argument of the
cosine in a more pleasing form:
2
1
E12 =  (1+ R ) + R1/2 cos (δ r + k r1 ⋅r − k t1 ⋅ r) ( E10( t ) ) .
2

The argument of the cosine in the above equation can be simplified if we note that
k1r =
(
)
(
)
2πn1
2πn1
−sinθ 1 iˆ − cosθ1 kˆ and k1t =
−sinθ1 ˆi + cosθ1 kˆ .
λo
λo
These relations can be found by analyzing the direction of the wave vector, k, in terms of the
direction vectors we have defined. Figure 3.4 illustrates this analysis for the transmitted portion
of the wave.
13
Interface 1
(top view)
kˆ
θ1
ˆi
−k1t sin θ1 iˆ
k1t cosθ 1kˆ
k1t
θ1
Figure 3.4: Finding the direction of the wave vector
The scalar product is distributive over addition and subtraction, so we can write
k1r ⋅r − k t1 ⋅r = ( k1r − k t1 ) ⋅r
=
(
)
2πn1
−2cosθ 1 kˆ ⋅r .
λo
Now r = x iˆ + yjˆ + zkˆ , so
(k
r
1
− kt1) ⋅r =
=
(
)
−4πn1
cosθ1kˆ ⋅ xiˆ + yjˆ + z kˆ
λo
−4πn1
cosθ 1z .
λo
Therefore:
1

2
4πn1

E12 =  (1+ R ) + R1/2 cos  δ r −
cosθ 1z  ( E10( t ) ) .

λo

2
14
(3.1)
This equation gives the time-averaged field intensities for the electric field in the incident
medium for s-polarized light. It is the first of nine equations that will be derived in this chapter
that will, together, completely describe electric field strengths in a thin film structure.
SUBSTRATE
We assume the substrate is semi-infinite in extent, so there is no reflected field. Therefore the
electric field in the substrate is just E m = E m0(t )e
(
i k tm ⋅r−ω t
)
,where E m0( t) is the total electric field
transmitted all the way through the stack, just inside the substrate.
We now need to make use of the total transmittance, t˜1′ . This is the “total” transmittance
calculated using equation (2.9) that takes multiple reflections into account. The subscript of this
variable is 1, which may seem odd since it represents the amount transmitted to the substrate
(layer m), but we adopt this convention since the recursive nature of equation (2.9) requires us
to work our way from “back to front” when calculating t˜1′ .
Now Em0( t) = t˜1′E10( t ) , and the time-average for the electric field in the substrate is
Em2 =
=
(
)
*
t
t
1
1
E m ⋅ E*m ) = t˜1′E10( t ) e i( k m ⋅r−ω t ) ⋅ t˜1′E10( t ) ei( k m ⋅r−ω t ) 
(

2
2
1 ˜ 2 0( t ) 2 i (k tm ⋅r −ω t) [ i(k tm ⋅r −ω t )]∗
t ′ (E1 ) e
⋅ e
.
2 1
∗
t
i (k t ⋅ r−ω t ) ]
Let us examine e i (k m ⋅r−ω t) ⋅ e [ m
to simplify.
∗
t
i (k t ⋅ r −ω t) ]
i( k t ⋅r −ω t )+ [i( k tm ⋅r −ω t ) ]
i kt ⋅r − iω t + [ i(k mt ⋅ r )]
e i(k m ⋅r −ω t ) ⋅ e [ m
=e m
=e m
*
*
−( iωt ) *
.
But ωt is real, so (iωt ) = −iωt , and therefore
*
e
i (k tm ⋅r−ω t )
⋅ e
[i (kmt ⋅ r−ω t )]
∗
=e
[
i ( ktm ⋅r)+ i(kmt ⋅ r)
]
*
.
Now let us simplify i( km ⋅ r) . Analyzing the direction of vector km, we can write
15
(
)
2π
(n − ik m ) sinθ˜m iˆ + cosθ˜mkˆ , and
λo m
km =
r = x iˆ + yˆj + zkˆ , so
i ( km ⋅ r ) = i
(
)(
)
2π
(n − ikm ) sin θ˜m iˆ + cosθ˜m kˆ ⋅ x iˆ + yˆj + zkˆ .
λo m
To simplify the derivation, we will now assume x = y = 0 . The x and y coordinates can be
chosen arbitrarily since z measures depth through the optical stack, and is thus the only
“meaningful” variable. So with this assumption we get
2πi
( nm − ik m ) cos θ˜m z .
λo
i( km ⋅ r) =
We now make a useful substitution that will only be used for a moment in this section but will
be quite helpful later in this chapter.
Let ξ˜m ≡ n˜ m cos θ˜m , so
i( k m ⋅r ) =
2πi ˜
ξ z.
λo m
We also need the complex conjugate of the argument, so we write
i( k m ⋅r ) =
[i (k
⋅r )] =
*
m
[
]
[
]
2πi
2π
ℜeξ˜ m + iℑmξ˜m z =
iℜeξ˜ m − ℑmξ˜ m z . Then
λo
λo
[
]
2π
−iℜeξ˜m − ℑm ξ˜m z, so
λo
i( km ⋅ r) + [i( km ⋅ r)] = −
*
(
)
4π
ℑmξ˜ m z ; therefore
λo
E
2
m
˜
2 − ( ℑmξ m ) z
1 2
= t˜1′ (E10( t) ) e λo
2
E
2
m
ℑm ( n˜ m cos θ˜m ) z
2 −
1 2
= t˜1′ (E10(t ) ) e λo
.
2
4π
4π
(3.2)
This is an expression for the electric field at depth z inside the substrate. In this equation we
can see that if n˜ m has an imaginary component, the electric field strength will decay
16
exponentially with distance into the substrate. This will occur when the substrate is an
absorbing medium. If the substrate is transparent, the exponential term is equal to 1.0, so the
field in the substrate is constant. Both cases will be investigated in Chapter IV.
INTERMEDIATE PHASES
Now let us consider the intermediate layers between the incident medium and the substrate. At
any interface, the E-field is transverse to the interface, so the total electric field is continuous
across each interface, i.e.
E (jt)− + E (j−r) = E (tj +) + E (rj +) .
(3.3)
The transverse component of the H-field is also continuous across each interface, which
corresponds to the x direction in our notation, so
H (tj−)x + H (r)
= H (tj+)x + H (j+r)x .
j− x
 ε˜ j 
The fields are related by H j =  
 µj 
1/2
Sˆ j × E j , where Sˆ j is a unit propagation vector pointing
in the direction of the wave flow. So in the jth medium,
 ε˜ j 
Hj = 
 µj
1/2
(Sˆ
(t )
j
×E
(t )
j
)
 ε˜ j 
+ 
µj 
1/2
(Sˆ
(r )
j
)
× E(jr ) , since Ej is the sum of the transmitted and
reflected wave. From the geometry of the incident and reflected waves we see that
Sˆ (jt ) = + cosθ˜j kˆ −sin θ˜ j ˆi
Sˆ (rj ) = −cosθ˜ j kˆ − sinθ˜ j iˆ ;
E (jt) = E (tj ) ˆj
E(jr ) = E (rj )ˆj .
Sˆ (jt ) × E (jt) = ˆi (Sy(t) Ez − Sz(t ) Ey ) + ˆj( S(zt ) Ey − Sx(t ) Ez ) + kˆ (S x(t ) E y − Sy(t )E x )
= − ˆi cos θ˜j E (j t) − kˆ sinθ˜ j E (tj ) .
Likewise,
Sˆ (jr) × E (rj ) = iˆ cosθ˜ j E (rj ) − kˆ sin θ˜ j E (rj ) .
17
 ε˜ j 
So H jx =  
µ j 
1/2
j
 ε˜ j 
= 
 µj 
H jx =
n˜ j cos θ˜ j
µj
[− cosθ˜ E
1/2
[− E
[ −E
(t)
j
(t)
j
( t)
j
+ cos θ˜ j E (rj )
]
]
+ E (j r) cosθ˜j
]
+ E (rj ) , the transverse component of the H-field in the jth medium.
At the interface between the jth and the (j+1) th medium (the jth interface), H j− x = H j + x . So
n˜ j cosθ˜ j
µj
[
]
−E (tj ) + E (rj ) =
n˜ j +1 cos θ˜ j +1
µ j +1
[−E
(t)
j +1
]
+ E j(r+1) .
Again using ξ˜ j ≡ n˜ j cosθ˜j , we get
ξ˜ j
µj
[E
(r )
j
−E
( t)
j
ξ˜ j+1
] = µ [E
( r)
j+1
]
− E j(t+1) .
j+1
But the electric fields are equal on either side of the interface so we can define
E (j r)+1 ≡ E (j +r) , Ej(t+1) ≡ E (tj+) and E (rj ) ≡ Ej(r− ), E (j t ) ≡ Ej(t−) .
In this new notation, the subscript “j” refers to the jth interface, with j − referring to the
incoming side of the interface, and j + referring to the “far” side of the interface.
In this notation we have
ξ˜ j
µ [
]
E (j −r ) − E (j −t) =
j
ξ˜ j+1
µ j+1
[E
( r)
j+
]
− E (j+t ) .
We combine this result with equation (3.3) to eliminate E (j +r ) and get
E (tj +) =
1  ξ˜j µ j +1  ( t ) 
1 + ˜
 E j − + 1 −
2 
ξ j+1 µ j 

ξ˜j µ j +1  ( r) 
Ej−  .
ξ˜ j+1µ j 

(3.4)
In like manner we can eliminate E (j +t ) to get
18
E (j +r) =
1  ξ˜ j µ j +1  ( t)  ξ˜j µ j +1  ( r) 
1 −
 E − + 1 + ˜
 Ej−  .
2  ξ˜j +1 µ j  j 
ξ j +1µ j 

(3.5)
These expressions allow one to propagate the transverse components of the E-field across an
interface if we know the reflected and transmitted E-fields on the “incoming” side of the jth
interface.
Using the fact that E (j +r) = r˜j′ E (j −t ) , where ˜rj′ is the reflection coefficient at the jth interface, and
equation 4.4, we can write
E (j +t ) =
1  ξ˜ j µ j +1   ξ˜ j µ j + 1   ( t )
1 +
 +  1−
 r˜ ′ E − .
2  ξ˜ j +1µ j   ξ˜ j+1 µ j  j  j
(3.6)
Similarly, with equation (2.7),
E (j +r) =
1  ξ˜ j µ j+1   ξ˜ j µ j +1   ( t )
1−
 +  1+
 r˜ ′ E − .
2  ξ˜ j+1 µ j   ξ˜ j+1 µ j  j  j
These equations are very useful since they take the transmitted portion of the field across the
interface.
We now need to describe the behavior of the field as it propagates through the jth medium from
the (j-1)th interface to the jth interface. The field inside the jth medium is composed of the initial
transmitted and reflected fields attenuated by exponential terms:
E j+1 = E (j +t )e
( ktj+1 ⋅r−ω t)
+ E (j+r) e
( krj+1 ⋅r− ω t)
.
Analyzing the geometry of the s-polarized light, we get
k tj +1 ⋅ r =
k rj +1 ⋅ r =
2πn˜ j +1
λo
2π n˜ j +1
λo
(−x sin θ˜
(−x sin θ˜
)
j +1
+ zcos θ˜ j+1 and
j +1
− z cosθ˜ j+1 .
)
19
Therefore
2πin˜
  ξ˜ µ  
ξ˜ j µ j+ 1   λoj +1 z cos θ˜j +1
1
j
j +1
E j +1 =  1 +
+ 1−
r˜ ′ e
˜ µ  
˜ µ  j 
2 
ξ
ξ
j+1 j
j +1 j

 
−2 πin˜ j+1
−2π in˜j +1
1  ξ˜ j µ j +1   ξ˜ j µ j+ 1   λo z cos θ˜j +1  −iω t λo x sin θ˜j +1 (t )
+ 1 + ˜
Ej − .
 +  1−
 r˜ ′ e
 ∗e e
2  ξ j +1 µ j   ξ˜ j+1 µ j  j 

−2πin˜ j +1
λo
We will now ignore e
x sin θ˜j +1 −iωt
since any numerical use of these equations necessitates
taking the absolute square of these fields which will cause us to calculate
−2πin˜ j +1
e
λo
*
 −2πin˜ j +1 x sin θ˜j +1 −iωt 
* e λo
 , which equals 1.


x sin θ˜j +1 −iωt
We will now substitute ϕ˜ j +1 =
e
iϕ˜ j+1
2πn˜ j +1 cos θ˜ j +1z
λo
=
2πξ˜ j+1 z
λo
and then use
= cosϕ˜ j +1 +i sin ϕ˜ j+1 to get


ξ˜ j µ j+ 1
E j +1 =  cos ϕ˜ j +1 1 + r˜j′ + i
sin ϕ˜ j +1 1 − r˜j′  Ej(t−) .
ξ˜ j +1 µ j


(
Recalling ϕ˜ j +1 =
E j +1
)
(
)
2πn˜ j +1 cos θ˜ j +1z ˜
, ξ j = n˜ j cosθ j , and ξ˜ j +1 = n˜ j +1 cosθ j +1 , we get
λo
  2π˜n j +1 cos θ˜ j +1z 
 n˜ j cos θ˜ j µ j +1   2π n˜ j +1 cosθ˜ j+1 z 

˜
˜
=  cos
 1 + rj ′ + i 
 sin 
 1 − rj ′  Ej(t−) .(3.7)
˜
λo
λo

 n˜ j +1 cosθ j+ 1µ j  

 

(
)
(
20
)
This equation gives the electric field within any intermediate layer. It requires knowledge of
E (j −t ) , which is the transmitted portion of the electric field, just before the interface that precedes
the desired intermediate layer. We will now derive an expression for E (j −t ) . The notation being
used is illustrated in the figure below.
E (jt−)
Layer:
..
E (jt+)
j
Interface:
)
E((tj +1
)−
.
j+1
j
j+1
Figure 3.5: The transmitted portion of the electric field at an interface
Starting with equation (3.6), we have
E (j +t ) =
1  ξ˜ j µ j +1   ξ˜ j µ j + 1   ( t )
1 +
 +  1−
 r˜ ′ E −
2  ξ˜ j +1µ j   ξ˜ j+1 µ j  j  j
.
(3.6)
This takes the transmitted portion of the field across an interface. Then we let E (jt+) propagate to
2πin˜j +1 cosθ˜ j+1
the (-) side of the next interface using
)
E((tj +1
)−
( t)
= Ej + e
of the (j+1) layer, to get
21
λo
lj +1
E (j t−) , where lj+1 is the thickness
2πin˜ j +1 cosθ j+ 1
lj+1
n˜ j cosθ˜ j µ j + 1  
n˜ j cos θ˜ j µ j +1  
1 
λo
1 −
˜ j′ e
= 1 +

+

r
E (j −t ) .
˜
˜
2 
n˜ j +1 cosθ j +1µ j  
n˜ j +1 cos θ j + 1µ j  
˜
E((jt)+1) −
P-Polarized Electric Field
For p-polarized light, the geometry of the incident and reflected fields looks like this:
kˆ
ˆi
ˆj
Et
Er
Sr
S0
Hr
E0
H0
Figure 3.6: Geometric relationships for p-polarized light
INCIDENT MEDIUM
First, we consider the incident medium, where we again assume n1 is real, i.e. k1 = 0. The total
field is the vector sum of the incident and reflected plane waves. We define E1 as the total
electric field in medium 1 and E10(t) as the incident p-polarized electric field intensity to get
E1 = E0(1 t )e
(
i k1t ⋅r −ω t
)
+ E 0(1 r )e
(
i k1r ⋅r −ω t
)
.
22
(3.8)
The components of E10(t) are E1x( t ) = cosθ1E1( t) and E1z(t ) = sinθ1 E1(t ) . The x-component of E10( t ) is
continuous across the interface since it is tangential to the interface. Since the magnetic field is
always tangential to the interface for p-polarized light we can write H1( r) = r˜1′H1(t) , where r˜1′ is
the “total” reflection coefficient for p-polarized light at the first interface and includes all layers
and multiple bounces beyond the first interface.
We also know
( t)
1
µ
=−  1 
 ε˜ 1 
(t)
1
 ε˜ 
= 1
 µ1 
E
H
1/2
1/2
(Sˆ
(t)
1
)
× H (1t ) and
 ε˜ 
Sˆ (1t ) ×E 1(t ) =  1 
 µ1 
(
)
1/2
( )
E1(t ) +ˆj .
We now want to calculate the total field.
(
)
E1(t) = cosθ 1 iˆ +sinθ 1 kˆ E1(t )
(
)
E1(r) = −cosθ1iˆ +sinθ 1kˆ E1( r ) . Now,
( r)
1
E
µ 
= − 1 
 ε˜1 
1/2
(Sˆ
( r)
1
)
× H1(r) with
Sˆ 1(r ) = −sinθ1 ˆi − cosθ1 kˆ
(
)
= − sinθ1 iˆ + cosθ 1kˆ and
H (1r ) = H1( r) ˆj . So
(Sˆ
(r )
1
)
× H1(r) = iˆ( Sy H z − Sz H y ) + ˆj( Sz H x − S x H z ) + kˆ ( Sx Hy − Sy H x )
= iˆ (cosθ1 H1(r ) ) + kˆ (−sinθ1 H1(r ) ) . Thus
23
( r)
1
E
µ 
= − 1 
 ε˜1 
1/2
[(cosθ )ˆi − (sinθ )kˆ ]H
1
1
( r)
1
, where we have used
 ε˜ 
H1( r) = r˜1′H1(t) = r˜1′ 1  E1(t) . So
 µ1 
[
]
E (1r ) = r˜1′ − cosθ 1ˆi +sin θ 1kˆ E1(t ) .
Therefore, the total electric field can now be written as
(
)
E1 = cosθ1ˆi +sinθ 1kˆ E1(t )e
(
i k1t ⋅r −ω t
)
(
)
+ r˜1′ − cosθ1 ˆi +sin θ 1kˆ E1(t ) e
(
i kr1⋅ r−ω t
)
.
Now we write the x and z components of E1, E1x and E1z .
(
E1x = cosθ 1 e

i k t1 ⋅r −ω t
E1z = sinθ 1 e

(
i k1t ⋅r −ω t
)
)
− r˜1′e
+ r˜1′e
(
i kr1⋅ r −ω t
(
) t
E
 1
) t
E .
 1
i k1r ⋅r−ω t
r
As we did with s-polarized light, we substitute r˜1′ = R1/2 e iδ and find the time-average:
E1x2 =
1
i ( kt ⋅r − k r ⋅r−δ r )
− i( k t ⋅r− k r ⋅r −δr ) 
 (E 0( t ) )2 .
cos 2 θ1 1 + R − R1/2  e 1 1
+e 1 1


 1
2
Substituting cosΦ =
E1x2 =
1 iΦ − iΦ
(e + e ) we obtain
2
[
]
2
1
cos 2 θ1 1 + R − 2R 1/2 cos( k1t ⋅ r − k1r ⋅ r − δ r ) (E10( t ) ) .
2
We simplify the argument of the cosine by using the geometry of the p-polarized electric field
components to get
k1t ⋅ r − k1r ⋅ r =
4πn1
cosθ1z .
λo
Therefore, we can find the final form for the tangential (x) component of the electric field,
24
E1x2 =

 4πn1
2
1

cos2 θ1 1+ R − 2R1/2 cos
cosθ 1z − δ r  (E10(t ) ) .
2
 λo


(3.8)
The normal (z) component of the electric field is found by taking
E1z2 =
1
E1z ⋅ E1∗z )
(
2
which similarly yields
E1z2 =

 4πn1
2
1

sin 2 θ 1 1+ R + 2R 1/2 cos
cosθ 1z − δ r  (E10( t ) ) .
2
 λo


(3.9)
These equations describe the tangential and normal components of the p-polarized fields in the
incident medium. If one wishes to know the combined p-polarized field strengths, this can be
found by simply taking E12 = E12x + E12z . This equation also applies in the substrate and
intermediate layers, though this is the only time it will be mentioned.
SUBSTRATE
The electric field in the substrate consists only of a traveling wave moving away from the last
interface, since we are assuming that the substrate is a semi-infinite medium. Anywhere in the
(
i k tm ⋅r−ω t
substrate the electric field can be written as E m = E(mt) e
)
, where E (mt ) is the component of
the electric field transmitted across the last interface and r is a position vector, measured from
the last interface pointing into the substrate.
We now need to calculate E (mt ) . The H-field vector is continuous across all interfaces since it is
always tangential for p-polarized light. We can then define a transmittance coefficient, t˜1H′ as
H (mt) = t˜1′H H10( t ) , where H 10 (t) is the amplitude of the H-field in the incident beam at the first
interface.
25
We recall that
H
 ε˜ 
= 1
 µ1 
0(t )
1
1/2
(Sˆ
0(t )
1
×E
0(t )
1
)
 ε˜ 
= 1
 µ1 
1/2
( )
E 10(t ) + ˆj .
Thus
H
 ε˜ 
= t˜1H
′  1
 µ1 
(t )
m
1/2
E10(t )ˆj .
Since
µ 
E = − m 
 ε˜ m 
1/2
(t )
m
(Sˆ
( t)
m
)
× Hm( t) and
Sˆ (mt) =− sinθ m iˆ +cos θ mkˆ , then
(S
ˆ ( t)
E
×H
m
(t)
m
(t )
m
)
 ε˜ 
= −t˜1H′  1 
 µ1 
 µ ε˜ 
= − m 1 
 ε˜ m µ1 
1/2
1/2
[
]
E10(t ) cosθ˜m ˆi +sin θ˜m kˆ . Therefore
[
]
t˜1H
′ E10(t ) cosθ˜m ˆi +sin θ˜ m kˆ ,
just across the boundary inside the substrate.
The field in the substrate a distance z from the last interface is
E
(t)
m
 µ ε˜ 
= − m 1 
 ε˜ m µ1 
1/2
[
]
i ( k ⋅r -ω t )
t˜1′H E10(t ) cos θ˜m iˆ +sin θ˜m kˆ e m
.
t
Breaking this field into its tangential component, Emx, and its normal component, Emz, we get
Emx
 µ ε˜ 
=  m 1
 ε˜ m µ1 
E mz
 µ ε˜ 
= m 1
 ε˜ m µ1 
1/2
1/2
i( k ⋅r-ω t )
t˜1′H E10(t ) cos θ˜m e m
t
i ( k ⋅r -ω t )
t˜1′H E10(t ) sin θ˜m e m
.
t
Now
26
 µ m ε˜1 


 ε˜ m µ1 
1/2
t˜1′H = t˜1E′ ,
due to the relations between the E- and H-fields for p-polarized light. So we get
(
)
i k mt ⋅r -ω t
E mx = t˜1E′ E10(t ) cosθ˜ m e
and
i( k ⋅r- ω t )
E mz = t˜1E
′ E10( t) sin θ˜m e m
.
t
We wish to calculate real measurable quantities, so we want to find time averages, i.e.
2
E mx
=
E mz ⋅ E
1
1
∗
2
E mx ⋅ Emx
and E mz
= ( E mz ⋅ E ∗mz ) .
(
)
2
2
∗
mz
{
}
(
)
∗ i ( ktm ⋅r-ω t ) 
*
i (k t ⋅r -ω t )

] 
= t˜1E′ E10( t ) cosθ˜m e m
* (t˜1′E ) E10( t ) cosθ˜ m e [


= t˜1′E
2
*
2
2
(E10( t ) ) cos θ˜m e i (k m⋅ r-ω t) +[i (km ⋅ r-ω t)] .
t
*
t
The argument of the exponential can be analyzed with a method identical to that which we used
to simplify the argument of the exponential in the s-polarized substrate equation, where we
derived the result:
i( km ⋅ r) + [i( km ⋅ r)] = −
*
(
)
4π
ℑmξ˜ m z .
λo
Thus:
2
1
= t˜1E′ cos θ˜m
2
2
E
2
mx
1
= t˜1E′
2
2
E
2
mz
2
sin θ˜ m
(E )
0( t) 2
1
(E )
0(t ) 2
1
−
e
−
e
(
)
4π
ℑm n˜ m cos θ˜m z
λo
(
)
4π
ℑm ˜nm cos θ˜m z
λo
.
INTERMEDIATE PHASES
27
(3.10)
(3.11)
We now want to calculate the electric field at any depth in an intermediate layer.
We write the total electric field anywhere in the (j+1) medium as
E j +1 = E (tj+) e
(
i k tj +1 ⋅ r−ω t
)
+ E (jr)+ e
(
i krj+1 ⋅r −ω t
)
.
We wish to make use of the fact that the H-field is continuous across the interface, so we need
to calculate E (j+t) and E (jr+) in terms of H.
E
(t )
j+
 µ j+1 

= −
 ε˜ j+1 
E
(r )
j+
 µ j +1 

= −
 ε˜ j +1 
1/2
(Sˆ
1/2
)
(t )
(Sˆ
× H(tj+) and
j+
( r)
j+
)
× H (jr)+ .
(
) (
(
) (
)
Sˆ (j t+) × H (jt+) = iˆ − cosθ˜ j+1 H (j +t ) − kˆ sin θ˜ j +1 H (j +t) and
)
Sˆ (j r+) × H (rj +) = iˆ cosθ˜ j+1 H (j +r) − kˆ sinθ˜j +1 H (rj+ ) , so
E
( t)
j+
 µ j+1 

=
 ε˜ j +1 
E
(r )
j+
µ 
=  j +1 
 ε˜ j +1 
1/2
1/2
[cos θ˜
j+1
[− cosθ˜
]
iˆ +sin θ˜j+1 kˆ H (j+t) and
]
ˆi +sin θ˜ kˆ H ( +r) .
j +1
j
j +1
Thus
E j+1
µ 
=  j +1 
 ε˜j +1 
1/2
 µ j +1 

+
 ε˜ j +1 
H (t+)ei ( k tj +1 ⋅r −ω t ) − H( +r )e i( k rj+1 ⋅r −ω t)  cosθ˜ iˆ
j +1
j
 j

1/2
H ( +t )e i( k jt +1 ⋅r −ω t) + H (r+ )e i (k rj+1 ⋅r −ω t ) sin θ˜ kˆ .
j+1
j
 j

Note that Ej+1 has a tangential (x) component and a normal (z) component:
28
1/2
E( j+1) x
 µ j+1 

=
 ε˜ j+1 
1/2
E( j+1) z
 µ j +1 

=
 ε˜ j +1 
H ( +t )e i( k tj +1⋅r −ω t ) − H (r+ ) e i( krj+1⋅r −ω t )  cosθ˜
j+1
j
 j

(3.12)
H (t+)e i( k jt+1 ⋅r −ω t ) + H ( +r) e i (k rj+1 ⋅r−ω t )  sinθ˜ .
j +1
j
 j

(3.13)
Just inside the jth interface,
E( j+1) x = E (tj +)x + E (j+r)x and E( j+1)z = E (j t+)z + E (j r+z) .
Let us define the sum of E-fields from incoming and outgoing light on one side of an interface
as
E j +x ≡ E (j+t)x + Ej(r+x) and E j − x ≡ E (j −t )x + E (rj −x) .
The tangential component of the electric field is continuous across an interface, so E j +x = E j −x ,
which can be related to equation 4.5 Single layer quarter wavelength AR coating: 72 nm layer HfO2
4.6 with
substrate with light incident at 30o and λ o = 550 nm. RS = 1.4% and
RP = 0.74%. An uncoated silicon substrate would have reflectances of
RS = 41.0% and RP = 30.6%
E j +x (new notation) = E( j+1) x (old notation) and
E j −x (new notation) = E jx (old notation) to yield
 µj 
 
 ε˜ j 
1/2
[H
(t )
j−
−H
(r )
j−
]
µ 
cosθ˜ j =  j +1 
 ε˜ j +1 
1/2
[H
( t)
j+
]
− Hj(r+ ) cosθ˜ j +1 .
We rewrite with ξ˜ j = n˜ j cosθ˜j , ξ˜ j+1 = n˜ j+1 cosθ˜ j +1 and n˜ 2j = µ j ε˜ j :
ξ˜ j
ξ˜ j +1 (t )
H j(t−) − H (j−r) =
H + − H (j+r) .
˜ε j
˜ε j +1 j
[
]
[
]
The magnetic field is all tangential, so
Hj(t+) + H (j +r) = H j(t−) + H(j −r ) , and we can eliminate one of these four variables Let us use
H j(r+ ) = H (j −t ) + H j(r−) − H (j +t ) to get
29
[
)]
ξ˜ j
ξ˜ j +1 (t )
(t )
( r)
H j − − H j− =
H j + − H (tj−) + H j(r− ) − H (tj+) , which we re-write as
ε˜ j
ε˜ j +1
[
]
(
 ξ˜ j ξ˜ j +1 
 ξ˜ j +1 ξ˜ j 
2ξ˜ j +1 (t )
(t)
( r)
 +
H
+

−
H
=
H+.
 j−
 j−
ε˜ j +1 j
 ε˜ j ε˜ j+1 
 ε˜j +1 ε˜ j 
Now H j(r− ) = r˜j ′H j(t−) , where r˜j ′ is the total reflection coefficient due to all interfaces beyond the jth
interface, so
 ξ˜ j ξ˜ j +1 
 ξ˜ j+1 ξ˜ j 
2ξ˜ j+1 (t )
(t)
(t)
 +
− H j− =
H+.
 H j− + r˜j ′
ε˜ j+1 j
 ε˜ j ε˜ j+1 
 ε˜ j+1 ε˜j 
We multiply by
ε˜ j+1
and collect terms to get
2ξ˜
j+1
H
(t )
j+
1  ε˜ j +1ξ˜ j   ε˜ j +1ξ˜ j   (t )
= 1 + ˜  + 1 − ˜  r˜j′H j − .
2  ε˜ j ξ j+1  
ε˜ jξ j +1  
(3.14)
We can similarly eliminate H j(t+) from the same equation to get
H
(r )
j+
ε˜ j+1ξ˜j   (t )
1  ε˜ j +1ξ˜ j  
= 1− ˜  +  1 + ˜  r˜j′H j − .
2 
ε˜ jξj+1  
ε˜ jξ j +1  
(3.15)
Tangential Component
These equations for H j(t+) and H j(r+ ) can now be substituted into equations 4.5 Single layer quarter waveleng
substrate with light incident at 30o and λ o = 550 nm. RS = 1.4% and
RP = 0.74%. An uncoated silicon substrate would have reflectances of
RS = 41.0% and RP = 30.6%
4.6 and (3.13). First, the tangential component:
E( j +1) x
µ 
=  j +1 
 ε˜j +1 
1/2
 1  ε˜ ξ˜   ε˜ ξ˜   i kt ⋅r −ω t
( j +1
)
j +1 j
j+1 j
 1 + ˜  +  1− ˜  r˜ j′e
2
ε˜ j ξj +1  
ε˜ jξ j+1  
 
30
1  ε˜ j +1ξ˜ j   ε˜ j+1ξ˜ j   i( kr ⋅ r− ω t ) 
(t )
− 1 − ˜  +  1+ ˜  r˜ j′e j +1
 cosθ˜ j +1H j − .
2  ε˜ j ξ j +1  
ε˜ j ξ j+1  

Let A =1 +
ε˜ j+1 ξ˜ j
ε˜ j +1ξ˜ j
and B =1 −
:
ε˜ ξ˜
ε˜ ξ˜
j
E( j+1) x
j +1
1  µ j +1 

= 
2  ε˜j +1 
j
1/2
j+1
cosθ˜ j+1 H (j −t) ( A+ Br˜j′)e

(
i ktj+1 ⋅r−ω t
)
− ( B + Ar˜j ′)e
(
i k rj +1⋅r−ω t
)
.

And as we had before,
k tj +1 ⋅ r =
k rj+1 ⋅r =
E( j +1) x
(
)
2πn˜ j+1
−xsin θ˜ j +1 + zcosθ˜ j +1 and
λo
2πn˜ j +1
λo
(−x sin θ˜
1  µ j +1 

= 
2  ε˜ j+1 
j+1
)
− zcos θ˜ j+1 , so
− 2πin˜ j +1
1/2
− (B + Ar˜ j′ )e
cos θ˜ j+1 H e
(t)
j−
−2 πi˜n j+1
λo
z cos θ˜j +1
−2πin˜j +1
We can again ignore e
Let ϕ˜ j+1 =
E( j+1) x
2π˜n j+1
λo
1/2
x sin θ˜j +1 −iωt
2πin˜ j +1

z cos θ˜j +1
λo
( A + B r˜j′)e


.

x sin θ˜ j+1 − iωt
, for the same reasons given before.
zcosθ˜ j +1 , and use e
1  µ j +1 

= 
2  ε˜j +1 
+i sin ϕ˜ j+1
λo
λo
{
[(A + Br˜ ′) + ( B + Ar˜ ′)]} .
iϕ˜ j+ 1
= cos ϕ˜ j +1 + i sin ϕ˜ j +1 to get
[
]
cosθ˜ j+1 H (j −t) cos ϕ˜ j+1 ( A + Br˜j ′) − (B + A r˜j ′)
j
A + B = 2 and A - B=
j
2 ε˜ j +1ξ˜ j
, so
ε˜ ξ˜
j
j +1
31
E( j +1) x
 µ j +1 

=
 ε˜ j +1 
 ξ˜ ε˜ 

j j +1
˜
˜
˜
˜
cos θ˜ j+1 H (j −t) 
cos
ϕ
1
−
r
′
+
i
sin
ϕ
1
+
r
′

j +1 (
j )
j +1 (
j ) .
˜
˜
ξ
ε
 j +1 j 

1/2
We now need to rewrite H j(t−) in terms of E (j −t ) .
H
( t)
j−
 ε˜ 
= j
 µj 
E( j +1) x
1/2
 ε˜ 
Sˆ (t) × E (tj −) =  j 
µj 
(
1/2
)
E (j −t ) ˆj . Thus
 µ j+1  1 / 2  ε˜ j+1  1 / 2
 

= cos θ˜ j +1  
˜
µ
ε



j
j 

 µ j+1 

+i 
 µj 
 ε˜ j 


 ε˜ j+1 
1/2
Now n˜ j = (µ j ε˜ j )
1/2
1/2
ξ˜ j
cos ϕ˜ j +1(1− r˜j′)
ξ˜
j +1

˜
˜
sin ϕ j+1 (1 + r j′) E (j −t ) .

and ξ˜ j = n˜ j cosθ˜ j , so

 2π˜n j +1 cos θ˜ j +1z 
 n˜ j cosθ˜ j+1 µ j +1   2π n˜ j +1 cos θ˜ j+1 z 

E( j +1) x = cos θ˜ j cos
(1− r˜j ′) + i
 sin 
 (1 + r˜j ′) Ej(t−)
λo
n˜ ( j+1) µ j
λo



 



(3.16)
This result gives the p-polarized electric field all through any intermediate layer. The field
intensities for the tangential component are continuous across each interface.
Normal Component
To calculate the normal component of the p-polarized E-field, we start with equation (3.13):
E( j +1) z
µ 
=  j +1 
 ε˜ j +1 
1/2
H (t+)ei ( k tj +1 ⋅r −ω t ) + H( +r )e i( k rj+1 ⋅r −ω t)  sinθ˜ .
j +1
j
 j

We now use equations (3.14) and 4.1 with the result
H
(t)
j−
 ε˜ j 
= 
 µj 
1/2
E (j −t ) ˆj .
32
(3.13)
1 µ 
=  j +1 
2  ε˜ j +1 
1/2
E( j +1) z
 ε˜ j 
 
 µj 
1/2
{
[
]
E (j −t ) sin θ˜ j +1 cosϕ˜ j +1 ( A + Br˜j′) + ( B + A r˜j ′)
]}
[
+i sin ϕ˜ j+1 (A + Br˜j′) − ( B + Ar˜j ′) ,
ε˜ j +1ξ˜ j
ε˜ j+1ξ˜ j
2π˜n j+1
with A =1 + ˜ , B =1 − ˜ , and ϕ˜ j+1 =
zcosθ˜ j +1 .
λo
ε˜ j ξ j+1
ε˜ jξ j +1
Simplifying as before, the result is
E( j+1) z
1  ε˜ j µ j+1 

= 
2  ε˜ j+1 µ j 
1/2
{
[
]
]}
[
E (j−t ) sinθ˜ j +1 cos ϕ˜ j+1 ( A+ B)(1+ r˜j ′) +i sin ϕ˜ j+1 ( A − B)(1− r˜j ′) .
2ε˜ j +1ξ˜ j
1/2
Substituting A + B =2; A - B = ˜
and using n˜ j = (µ j ε˜ j ) and ξ˜ j = n˜ j cosθ˜ j , we obtain
ε˜ ξ
j
E( j+1)z
j+1

 n˜ j µ j +1 
 cos θ˜ j 
( t)
˜
˜
.

˜
˜

˜

sin
ϕ
1
−
r
′

= sin θ j +1 
cos ϕ j +1 (1 + r j′) +i
j +1 (
j )  E j−
˜
˜
n
µ
cos
θ




j+1
j
+1
j


Now n˜ j+1 sin θ˜ j+1 = n1 sinθ 1 , which is real, so we substitute this into the expression and get
 n˜ j µ j+1 
 2π n˜ j +1 cos θ˜ j+1 z
 cos θ˜ j   2π n˜ j +1 cos θ˜ j +1 z 

(t)
 cos 
sin
1− r˜ j′) E j −
E( j +1) z = (n1 sinθ 1)  2
 (1 + r˜j′) + i


(
˜
˜
λo
λo

 n˜ j +1 cos θ j+1  

 n j+1 µ j  

(3.17)
This result gives the p-polarized electric field through any intermediate layer. The field
intensities for the normal component are not continuous across each interface.
We need an expression for E (jt−) , as we did for s-polarized light. Starting with equation (3.14),
H
(t )
j+
1  ε˜ j +1ξ˜ j   ε˜ j +1ξ˜ j   (t )
= 1 + ˜  + 1 − ˜  r˜j′H j −
2  ε˜ j ξ j+1  
ε˜ jξ j +1  
.
(3.14)
2 πi˜n j+1 cosθ˜j +1
We let Hj(+t) propagate to the (-) side of the (j+1) interface using H((j+t) 1)− = e
where lj+1 is the thickness of the (j+1) layer, to get
33
λo
l j +1
H (jt−) ,
H((tj+) 1)−
2πin˜j +1 cosθ˜ j+ 1
l j +1
ε˜ j+1 ξ˜ j  
1  ε˜ j +1ξ˜ j  
λo
˜
= 1+
+
1
−
r
′
e
H (j −t) .
 
 j
˜
˜
2 
ε˜ j ξ j+1  
ε˜ j ξ j +1  

)
Substituting as above and with H j(t−) = n˜ j E(j −t ) and H((tj+) 1)− = n˜ j +1 E(( jt +1
, we get
)−
2πin˜j +1 cosθ j+ 1
l j +1
n˜ j +1 cos θ˜ j  
n˜ j +1 cos θ˜ j  
1  n˜ j  
λo
 1 +
=
 +  1−
 r˜ j′e
E (j −t ) .
2  n˜ j +1  
n˜ j cosθ˜ j+1  
n˜ j cos θ˜ j + 1  
˜
(t)
E( j +1) −
(3.18)
EQUATION SUMMARY
We have now derived nine equations that allow one to calculate electric field strengths for s- or
p-polarized light propagating through a multilayer thin film structure. The table of equations on
the following page lists these equations in the order they were derived.
34
Equation Summary
S-POLARIZED
incident
1

2
4πn1

E12 =  (1+ R ) + R1/2 cos  δ r −
cosθ 1z  ( E10( t ) )

λo

2
(3.1)
substrate
4π
1 ˜ 2 0(t ) 2 − λo ℑm ( n˜ m cos θ˜m ) z
2
E m = t1′ (E1 ) e
2
(3.2)
intermediate
4.1
(3.7)
P-POLARIZED
incident
4.1
4.
E1z2 =

 4πn1
2
1

sin 2 θ 1 1+ R + 2R 1/2 cos
cosθ 1z − δ r  (E10( t ) )
2
 λo


(3.8)
substrate
4.
4.1
E
2
mz
1
= t˜1E′
2
2
sin θ˜ m
2
(E )
0(t ) 2
1
−
e
(
)
4π
ℑm ˜nm cos θ˜m z
λo
(3.11)
intermediate

 2π˜n j +1 cos θ˜ j +1z 
 n˜ j cosθ˜ j+1 µ j +1   2π n˜ j +1 cos θ˜ j+1 z 

˜
˜
˜
E( j +1) x = cos θ j cos
(1− rj ′) + i
 sin 
 (1 + rj ′) Ej(t−)
λo
n˜ ( j+1) µ j
λo



 



(3.16)
 n˜ j µ j+1   2π n˜ j+1 cos θ˜ j +1 z 
 cos θ˜ j   2π n˜ j+1 cos θ˜ j +1 z 

(t)
 cos
sin
1 − r˜j′) E j −
E( j+1)z = (n 1 sin θ 1 )  2
 (1 + r˜j′) + i 


(
˜
˜
λo
λo

 n˜ j +1 cos θ j+1  

 n j+1 µ j  

(3.17)
35
Chapter IV
Numerical Analysis
In this chapter we will use the equations just derived to generate graphs illustrating electric field
strengths for several thin film structures. We will choose examples that illustrate several
common thin film design goals and strategies.
Two Layers on an Absorbing Substrate
For an introduction to the form and function of electric field plots, we first consider a thin film
structure consisting of two intermediate layers. For incident light of wavelength 550 nm, we
will let air be the incident medium, the first layer will be crystalline silicon ( n˜ = 3.9822 - 0.0334
i) with a thickness of 400 nm, the second layer will be a 400 nm layer of Al2 O3 (n = 1.6203),
and the substrate will be GaAs ( n˜ = 4.047 - .324 i). The light is incident on the first interface at
an angle of 45o .
36
45o
Air
Crystalline Silicon
Al2 O3
400 nm
400 nm
GaAs Substrate
Figure 4.1: Diagram of a thin film
The graph of the electric field strengths for this example is given in Figure 4.2.
37
Air
Silicon
Pz2Al2 O 3
Pz3
Pz4
GaAs
3
E
S
2
(E )
Px
0 ()t 2
1
Pz
2
1
0
Depth (nm)
Figure 4.2: Electric field strengths for a thin film consisting of 400 nm Si, 400 nm Al2 O3 on a
GaAs Substrate, with light incident at 30o and λ o = 550 nm
To see the detail of the field strength plot in the intermediate layers and substrate, we enlarge the
vertical scale:
38
Air
Pz2Al
Pz3
Pz4
Silicon
2
0.4
O3
GaAs
S
0.3
E2
(E )
0 ()t
1
Px
Pz
2
0.2
0.1
0
Depth (nm)
Figure 4.3: Detail of Figure 4.2
To generate the data graphed above, the following sequence was followed:
1. Propagation angles for light at each layer were calculated using Snell’s law.
2. Fresnel’s reflection and transmission coefficients were calculated at each interface, for both
s- and p-polarized light.
3. Rouard’s expression was used to find a total reflectance and transmittance for the stack.
4. δ r was calculated for the s- and p-polarized cases.
5. The electric field equations were programmed and numerical values for the electric field
strengths were generated.
All of the above numerical calculations were performed using Mathematica. Data were then
exported to CA-Cricket Graph III to generate the graphs in this paper.
39
The field strengths are given as relative values, which is equivalent to graphing E 2 with the
(
assumption that the incident intensity of the light E10 ( t)
)
2
is equal to one.
In the graph above, one can note that the field strengths of the s-polarized light and the x
component of the p-polarized light are both continuous at the interfaces, as Maxwell’s equations
require for tangential field components. The z component of the p-polarized light is obviously
discontinuous.
In all layers that precede the substrate, the electric field strength plot is oscillatory. This is not a
“stop action” picture of the light waves, but rather the time average of the electric field. The
plot is oscillatory because of interference between the reflected and transmitted portions of the
incident light. There is no oscillation in the substrate because there is no reflected field to
interfere with the transmitted field, so the time-averaged plot of the transmitted light merely
decays because of the absorptive properties of GaAs.
The field strength plot in the silicon layer shows an oscillation that is attenuated because silicon
is an absorbing material. Since n˜silicon ≠ ℜe( n˜ silicon ) , the exponential terms in our equations “die
out” as z increases. The field also “dies out” in the substrate, but does not do so in the air and
Al2 O3 , which are transparent.
Single Layer AR Coating
40
One of the simplest common thin film structures is a quarter wavelength single layer antireflective (AR) coating. AR coatings are commonly used on optical instruments where it is
important to increase the transmission of light. They work through the well-known mechanism
of destructive interference that occurs between light waves that reflect off the front surface of the
coating and those that reflect off its back surface. If the layer thickness is equal to a quarter
wavelength, the destructive interference is maximized. It is to be noted that the quarter
wavelength thickness is determined by the wavelength of the light in the material, which in this
example we label as λ 1 .
In Figure 4.4, we see the electric field strength plot for a single layer AR coating with the
following parameters: λ o = 550 nm, incident medium is air (n = 1.00), the single intermediate
layer is HfO2 (n = 1.916), substrate is silicon ( n˜ = 3.98 - .0334 i). The thickness of the
intermediate layer is 72 nm (λ 1 / 4). The incident angle of the light is 0o . At normal incidence,
there is no z component of the p-polarized light. Furthermore, the x component of the ppolarized light becomes identical to s-polarized light so the graph contains only a single line.
The reflectance for this design is quite low, R = 0.17%. In comparison, an uncoated silicon
substrate would have a reflectance of R = 36% at normal incidence.
41
Air
HfO2
Silicon
1.25
S
1
E2
Px
(E )
0 ()t
1
Pz
2
0.75
0.5
0.25
0
Depth (nm)
Figure 4.4: Single layer quarter wavelength AR coating: 72 nm layer HfO2 on Si substrate
with light at normal incidence and λ o = 550 nm, R = 0.17%. Uncoated silicon
substrate: R = 36%.
We note that the electric field strength in the incident medium oscillates about a value of
approximately 1.0, which is the incident intensity. This makes sense, since the reflectance is
low enough that there should not be much of a reflected field to increase the field strength
values in the air. If the reflectance had been very high, we would expect the field to oscillate
about a value of approximately two, since that would be the value of the sum of the incident and
reflected fields.
42
Next, we use the same design, but make the incident angle 30o . These parameters yield total
reflectances of RS = 1.4% and RP = 0.74%. An uncoated silicon substrate would have
reflectances of RS = 41.0% and RP = 30.6% at this angle of incidence.
Pz3
Pz2
Air
HfO2
Silicon
1.25
S
E
(E )
0 ()t
1
Px
1
2
Pz
2
0.75
0.5
0.25
0
Depth (nm)
Figure 4.5: Single layer quarter wavelength AR coating: 72 nm layer HfO2 on Si substrate
with light incident at 30o and λ o = 550 nm. RS = 1.4% and RP = 0.74%. An
uncoated silicon substrate would have reflectances of RS = 41.0% and RP = 30.6%
The anti-reflective properties of the film become much less effective if the layer thickness is not
equal to a quarter wavelength. Figure 4.6 was created with parameters identical to those used to
produce Figure 4.5, except the layer thickness was set at 150 nm. This thickness is close to a
half wavelength, which is a very bad AR design. The reflectances for this design are RS =
41.0% and RP = 30.6%, which are nearly identical to an uncoated silicon substrate.
43
Air
Pz2
HfO2Pz3
Silicon
3
2.5
S
E2
(E )
0 ()t
1
2
2
Px
Pz
1.5
1
0.5
0
Depth (nm)
Figure 4.6: Imperfect single-layer AR coating: 150 nm layer HfO2 on Si substrate with light
incident at 30o and λ o = 550 nm. . RS = 41.0% and RP = 30.6%.
In comparing this plot to Figure 4.5, we note the much higher reflected field in the incident
medium due to the imperfect layer thickness. Since the HfO2 layer is not a quarter-wave, the
multiple reflections are not out of phase and they add, generating a large reflected wave.
Dielectric HR Mirror
Another interesting example to consider is a high reflectance structure composed only of
dielectric materials. One common design that is used for this purpose is a thin film stack
44
composed of quarter-wavelength layers that alternate between high and low-index materials, as
illustrated in the following figure.
Incident
Medium
High
Inde
x
Low
Inde
x
High
Inde
x
Low
Inde
x
λ H/4
λ L/4
λ H/4
λ L/4
Repeated Pattern ...
Substrate
Figure 4.7: Schematic of a design for a dielectric HR mirror
Thin film structures with a large number of repeated high-low stacks can be made to maximize
reflectance for a given wavelength.
Figure 4.8 shows the electric field within an eight layer stack containing alternating layers of
TiO2 (n = 2.2303) and MgF 2 (n = 1.3862) on a glass substrate for an incident angle of 30o and
light with a wavelength of 550 nm. Each layer is a quarter wavelength thick at 30o incidence (60
nm for TiO2 and 100 nm for MgF2 ), which yields reflectances of RS = 95.9% and RP = 90.4%,
for the given wavelength and angle of incidence.
45
Air
Pz9
Pz4
TiO2 MgF 2 TiO2 MgF 2 TiO2 MgF 2 Pz10
Pz5
Pz3
Pz6
Pz7
Pz8
TiO2 MgF 2 Glass
Pz2
4
S
Px
Pz
3
E
2
(E )
0 ()t 2
1
2
1
0
Depth (nm)
Figure 4.8: A dielectric high reflectance structure: Eight alternating layers of quarter
wavelength layers of TiO2 and MgF2 on glass substrate with light incident at 30o
and λ o = 550 nm. RS = 95.9% and RP = 90.4%.
Here we see the s-polarized field with a maximum value near 4.0, so its average value is almost
2.0, which is the value we would obtain for a perfect mirror.
Critical Angle
We now consider the critical angle. As light passes from a higher index material into one that
has a lower index, the beam is refracted away from the normal, as predicted by Snell’s Law. As
the incident angle is increased, an angle is eventually reached where the beam is refracted so
much that the refracted angle becomes greater than ninety degrees. At this point, the beam is
46
“trapped” inside the higher index incident medium, and does not pass through the interface at
all, but instead exhibits total internal reflection. We consider a system where light travels from
glass (n = 1.5) into air with an incident wavelength of 550 nm (in air). First, Figure 4.9 shows a
graph of the reflectance of the light plotted vs. the incident angle. The reflectance goes to 1.0 at
the critical angle of 41.8o .
100
90
Reflectance
(%)
80
S
70
P
60
50
40
30
20
10
0
Incident Angle
(degrees)
Figure 4.9: Reflectance vs. angle for light traveling from glass into air
Next, we graph the electric field strengths for light at an incident angle of 40o , which is just
lower than the critical angle.
47
Glass
Pz2
Air
4
S
3
E
2
Px
Pz
(E )
0 ()t 2
1
2
1
0
Depth (nm)
Figure 4.10: Electric field strengths for glass to air at 40o with λ o = 550 nm
In the graph above, we note the constant electric field values in the substrate. The field strength
is constant because there is only a transmitted field, with no reflected field to interfere with it
and cause oscillations. There is also no absorption in the substrate.
In Figure 4.11, the parameters are the same, except the incident angle is 45o . This is greater
than the critical angle, so the light is totally reflected at the interface.
48
Pz2
Glass
Air
6
S
Px
5
Pz
4
E2
(E )
0 ()t
1
2
3
2
1
0
Depth (nm)
Figure 4.11: Electric field strengths for glass to air at 45 o with λ o = 550 nm
The field plots in Figure 4.11 are quite interesting. The s-polarized field intensity in the
incident medium has maxima at exactly 4.0, which tells us that the average value of the field is
2.0. This corresponds to 100% reflection. Furthermore, the sum of the components of the ppolarized light is also two, so the p-polarized light is 100% reflected as well.
In the substrate, we see that the field intensities “die off” exponentially past the interface, even
though air is a transparent medium. Mathematically, this occurs because the refracted angle is
imaginary, so the argument of the exponential term in the substrate equations is not zero. But in
this case the imaginary portion of the argument is not a consequence of the physical properties
of the substrate, but results from the geometric relationships that occur due to the refraction of
the light. To further elaborate, we have Snell’s law, Equation (2.2): n˜1 sin θ˜1 = n˜ 2 sin θ˜2 . In this
49
example, n1 = 1.5, θ1 = 45o , and n2 = 1. Substituting these values into Snell’s Law, we get
sin θ˜ 2 = 2 ≅1.414 . The only way the value of the sine can be greater than one is for the
refracted angle to be imaginary, particularly θ˜2 ≅ (1.57 − .881i ) . Thus we acquire the non-zero
argument for the exponential in the substrate equations.
It may seem odd that there is any field in the substrate medium at all, since the reflection at the
interface is 100%. But energy is conserved since no energy propagates away from the
interface. The energy in the substrate medium propagates parallel to the interface, and is thus
present as a sort of “phantom field.”
Finally, we note that the z component of the p-polarized electric field is very high on the
outgoing side of the interface, exceeding a value of 6.5 in our example. Thin film designers
must be aware of this when working with designs intended for high-intensity applications, such
as high energy lasers. Problems can occur at the interface in a number of ways. For instance, if
there is a particle impurity in the film near the interface, such as a dust mote, the high fields at
the critical angle can vaporize the particle in a “flash” of energy, possibly damaging the film.
Damage can also be magnified if the film contains cracks or scratches, since electric fields are
further increased by “edge effects.”
Plasmon Resonance Angle
In this section we will consider a system where the incident medium is quartz, the intermediate
medium is a 50 nm layer of silver ( n˜ = 3.7681 - .04115 i at λ o = 550 nm), with an air substrate.
Figure 4.12 is a plot of the reflectance of this structure vs. the incident angle of the light.
50
100
75
Reflectance
(%)
S
50
P
25
0
Incident Angle
(degrees)
Figure 4.12: Reflectance vs. incident angle for light traveling from quartz through a 50 nm
layer of silver into air with λ o = 550 nm
The sharp “dip” in the p-polarized reflectance occurs at the plasmon resonance angle. This
occurs because at this particular angle the free electrons in the silver at the interface experience
oscillations that are greatly augmented by the geometrical relationship that exists between them
and the p-polarized electric field vectors. The electrons oscillate and absorb the light, thus
decreasing the reflectance of the thin film. These free electrons are referred to as a surface
“plasmon” since they are part of a crystal lattice but still have some freedom of motion and are
thus similar to a plasma. The s-polarized light is unable to excite these exaggerated oscillations
because its field vector is tangential to the interface and it cannot “couple” to the plasmon field.
First, we plot the field intensities for the above system at an incident angle of 40o :
51
Quartz
Pz3
Pz2
Silver
Air
4
S
Px
3
Pz
E2
(E )
0 ()t
1
2
2
1
0
Depth (nm)
Figure 4.13: Electric field strengths for light traveling from quartz through a 50 nm layer of
silver into air at 40o incident angle with λ o = 550 nm
The above plot is consistent with a fairly ordinary high reflectance structure, with absorptive
attenuation in the silver layer and relatively low transmitted intensities in the air substrate.
We now examine the electric field distribution at the surface plasmon resonance. At the
plasmon resonance angle (θ1 ≅ 45.3o ), we see much greater penetration of the field for the ppolarized light.
52
Quartz
Pz2
Silver
Air
25
S
Px
20
E2
(E )
0 ( t)
1
Pz
2
15
10
5
0
Depth (nm)
Figure 4.14: Electric field strengths for light traveling from quartz through a 50 nm layer of
silver into air at 45.3o incident angle with λ o = 550 nm
In Figure 4.14, we note that the s-polarized light is highly reflected, but the p-polarized light is
transmitted into the silver quite efficiently. The plot of the z component of the p-polarized light
is not visible in the substrate because the relative value of the field strength exceeds 300 just
across the interface. At the plasmon resonance angle, the geometrical relationships between the
p-polarized electric fields and the free electrons in the silver are such that there is a very efficient
coupling between the two, because of energy and momentum conservation for the p-polarized
light. The resonant oscillations of the free electrons cause the very strong fields that occur at
the interface, which a thin film designer would need to be aware of when working with designs
of this sort.
53
Transmittance Properties of Copper
For our final example, we briefly observe how the transmittance properties of copper vary with
wavelength. We will compare two electric field plots for light incident on a 50 nm layer of
copper on a glass substrate, one where the incident wavelength is 500 nm, and one with an
incident wavelength of 1000 nm.
When λ o = 500 nm, the optical constant for copper is n˜ = 1.1411 - 2.5718 i. In this
configuration, TS = 2.4% and TP = 3.1%.
Air
Pz3
Pz2
Copper
Glass
4
S
E
2
(E )
0 ( t)
1
3
Px
2
Pz
2
1
0
Depth (nm)
Figure 4.15: Electric field strengths for a 50 nm layer of copper on glass at 30o with λ o =
500 nm
The reflectivity of the above structure is RS = 62% and RP = 53%. We note that R + T ≠ 100%
since copper is an absorbing medium.
54
For Figure 4.16, when the incident wavelength of the light is 1000 nm and n˜ = 0.3616 - 6.3181
i, we have TS = .51%, TP = .74%, RS = 96% and RP = 94%.
Air
Pz3
Pz2
Copper
Glass
4
S
Px
3
E
(
2
E10 ( t)
)
Pz
2
2
1
0
Depth (nm)
Figure 4.16:
Electric field strengths for a 50 nm layer of copper on glass at 30o with λ o =
1000 nm
The plot shows that the field in the incident medium is much higher than in the previous graph,
indicating a reflectivity that is nearing 100%. We have found that the reflection and
transmission characteristics for a structure can be very dissimilar for light of different incident
wavelengths.
55
Chapter V
Summary
In this paper we have derived equations that calculate electric field strengths in a multilayer thin
film structure. Starting with several important equations that describe the electric field, we made
use of several physical principles to motivate the derivation, especially reflection and
transmission coefficients at interfaces, and the continuity of tangential field components. The
equations were simplified using basic rules of algebra and vector calculus, and an effort was
made to make the notation logical and consistent throughout the paper. The equations are
recursive, and can be used for any arbitrary number of intermediate layers. They are in a form
that is well-suited to numerical analysis with a computer.
After the equations were derived, they were used to calculate the fields for a variety of thin film
designs, showing the behavior of the electric field in several interesting situations. The
oscillatory nature of the time-averaged electric field strengths in thin films that have a reflected
field was evident in our graphs. We investigated an AR and a HR design. We observed the
interesting field penetration effects that occur near the plasmon resonance angle for a thin metal
layer. We saw the field that exists beyond an interface that is exhibiting total internal reflection
for light incident at angles greater than the critical angle. The transmittance properties of two
wavelengths of light passing through a thin copper layer were compared.
The numerical analysis in this paper was a mere “dip” into the enormous field of thin film
optical design applications. The examples included in this paper were chosen to exemplify a
few simple examples that make use of the derived equations, but do not represent a thorough
56
study of thin film optics. While the main work of this paper was to actually derive the
equations “from scratch,” the equations represent a useful tool to further investigate deeper and
more interesting questions of thin film design.
57
References
1. Jackson, John David, Classical Electrodynamics, Second Edition; John Wiley and Sons:
New York, 1975, p. 271.
2. Klein, Miles V., Optics; John Wiley and Sons: New York, 1970, p. 534
3. Anders, Hugo, Thin Films in Optics; The Focal Press: London, 1965, p. 15
4. Ref. 1, p. 280
5. Macleod, H.A., Thin-Film Optical Filters; American Elsevier: New York, 1969, p. 14
6. Ref. 5, p. 10
7. Ref. 2, p. 568
8. Ref. 3, p. 19
9. Born, Max and Wolf, Emil, Principles of Optics; Third Edition; Pergamon Press: Oxford,
1965, p. 40.
10. Ref. 9, p. 40
11. Ref. 3,p. 59
12. Hansen, Wilford N., Opt. Soc. Am. 58; 381 (1968).
58