* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download average power - Department of Electrical Engineering
Valve RF amplifier wikipedia , lookup
Power MOSFET wikipedia , lookup
Radio transmitter design wikipedia , lookup
Standby power wikipedia , lookup
Power electronics wikipedia , lookup
Audio power wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Rectiverter wikipedia , lookup
Captain Power and the Soldiers of the Future wikipedia , lookup
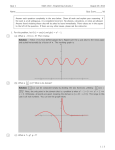
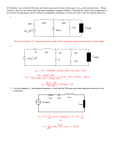
Chapter 11 AC Steady-State Power Matching Network for Maximum Power Transfer Cellular Telephone Design the matching network to transfer maximum power to the load where the load is the model of an antenna of a wireless communication system. George Westinghouse, 1846-1914 The greatest engineer of his day, George Westinghouse modernized the railroad industry and established the electric power system. Nikola Tesla, 1856-1943 Tesla was responsible for many inventions, including the ac induction motor, and was a contributor to the selection of 60Hz as the standards ac frequency in the United States. Instantaneous Power and Average Power Instantaneous Power p (t ) v (t ) i (t ) A circuit element If v(t) is a periodic function v (t ) v (t T ) Then for a linear circuit i(t) is also a periodic function i (t ) i (t T ) p (t ) v (t T ) i (t T ) Instantaneous Power and Average Power(cont.) Average Power 1 P T t0 T p(t ) dt t0 Arbitrary point in time If v(t) is a sinusoidal function v(t ) Vm (cos t V ) For a linear circuit i(t) is also a sinusoidal function i (t ) I m (cos t I ) p(t ) Vm I m (cos t V )(cos t I ) Vm I m p (t ) cos(V I ) cos(2 t V I ) 2 T 1 Vm I m P cos(V I ) cos(2 t V I ) dt T 0 2 T T 1 Vm I m 1 Vm I m cos(V I ) dt cos(2 t V I ) dt T 0 2 T 0 2 T T Vm I m 1 Vm I m cos(V I ) dt cos(2 t V I ) dt 2T T 0 2 0 Vm I m cos(V I ) 0 2 Vm I m cos(V I ) 2 average value of the cosine function over a complete period is zero Example 11.3-1 P=? Using the period from t = 0 to t = T Im i t ;0t T T i(t) through a resistor R The instantaneous power is 2 Im R 2 pi R 2 t T ;0t T 2 The average power is 2 1 Im R 2 P t dt 2 T 0 T T 2 2 3 2 Im R Im R T Im R 2 P 3 t dt 3 0 T T 3 3 T W Example 11.3-2 PL = ? PR = ? i (t ) 721cos(100t 41) mA The element voltages are vs (t ) 20cos(100t 15) V vR (t ) 18cos(100t 41) V vL (t ) 8.66cos(100t 49) V The average power delivered by the voltage source is (20)(0.721) Ps cos( 15 ( 41)) 6.5 W 2 The average power delivered to the voltage source is 6.5 W Example 11.3-2 (cont.) The average power delivered to the resistor is (18)(0.721) PR cos( 41 ( 41)) 6.5 W 2 The average power delivered to the inductor is (8.66)(0.721) PL cos(49 ( 41)) 0 W 2 WHY the average power delivered to the inductor = 0 ? The angle of vL always be 90larger than the angle of iL and cos(90) 0 Effective Value of a Periodic Waveform The goal is to find a dc voltage, Veff (or dc current, Ieff), for a specified vs(t) that will deliver the same average power to R as would be delivered by the ac source. The energy delivered in a period T is W PT The average power delivered to the resistor by a periodic current is 1 T P T 0 i 2 Rdt Effective Value of a Periodic Waveform (cont.) The power delivered by a direct current is PI R 2 eff 1 P T Solve for Ieff T 0 i Rdt I R 2 2 eff 1 T 2 I eff i dt T 0 I rms rms = root-mean-square The effective value of a current is the steady current (dc) that transfer the same average power as the given time varying current. Example 11.4-1 Ieff = ? Express the waveform over the period of t = 0 to t = T Im i t ;0t T T i(t) = sawtooth waveform I eff 1 T 2 1 T I m2 2 i dt t dt 2 T 0 T 0 T T I t 3 T T 0 2 m 3 3 I eff 2 m I 3 Im 3 Complex Power A linear circuit is excited by a sinusoidal input and the circuit has reached steady state. The element voltage and current can be represented in (a) the time domain or (b) the frequency domain Complex Power (cont.) To calculate average power from frequency domain representation of voltage and current i.e. their phasors I( ) I m I and V( ) VmV The complex power delivered to the element is defined to be VI ( I m I )(VmV ) S 2 2 I mVm (V I ) 2 * Apparent power where I complex conjugate of I * Complex Power (cont.) The complex power in rectangular form is I mVm I mVm S cos(V I ) j sin(V I ) 2 2 P Q or S P jQ real or average power reactive power Units S : VA, P:W, Q:VAR Volt-Amp Volt-Amp Reactive Complex Power (cont.) The impedance of the element can be expressed as V ( ) VmV Vm Z( ) (V I ) I( ) I m I I m In rectangular form Vm Vm Z( ) cos(V I ) j sin(V I ) Im Im R X or Z( ) R jX resistance reactance Complex Power (cont.) The complex power can also be expressed in terms of the impedance I mVm I mVm S cos(V I ) j sin(V I ) 2 2 2 2 I m Vm I m Vm cos(V I ) j sin(V I ) 2 Im 2 Im I 2 2 m Re( Z) P I j 2 2 m Im( Z) Q Complex Power (cont.) The impedance triangle The complex power triangle The complex power is conserved all elements * k k VI 0 2 The sum of complex power absorbed by all elements of a circuit is zero. Complex Power (cont.) The complex power is conserved implies that both average power and reactive power are conserved. * VI V I k k 0 Re 2 2 all all elements elements * V I k k Re 0 2 all elements * V I Im k k all 2 elements * V I k k Im 0 2 all elements * k k and or all elements Pk 0 and all elements Qk 0 Example 11.5-1 S is conserved ? vs 100cos1000t V =1000 Solving for the mesh current Vs I( ) 7.07 45 1 R j L j C Use Ohm’s law to get the element voltage phasors VR ( ) RI( ) 70.7 45 VL ( ) j LI( ) 141.445 j VC ( ) I( ) 70.7 135 C Example 11.5-1 (cont.) Consider the voltage source Vs I* supplied by the source SV 2 353.545 VA For the resistor VR I* SR absorbed by the resistor 2 2500 VA For the inductor VLI* delivered to the inductor SL 2 50090 VA Example 11.5-1 (cont.) For the capacitor VC I* delivered to the capacitor SC 2 250 90 VA The total power absorbed by all elements (except source) S R S L SC 2500 50090 250 90 353.545 SV For all elements all elements Vk I*k 0 2 Example 11.5-2 P is conserved ? vs 100cos1000t V =1000 The average power for the resistor, inductor, and capacitor is I m2 P Re( Z) 2 I m2 PR R 250 W PL PC 0 2 The average power supplied by the voltage source is Vs I* PV Re SV Re 2 Re(353.545) 250 W Power Factor The ratio of the average power to the apparent power is called the power factor(pf). I mVm average power P cos(V I ) 2 S apparent power pf cos (V I ) pf angle Therefore the average power I mVm P pf 2 Power Factor (cont.) The cosine is an even function cos( ) cos( ) pf cos(V I ) cos( I V ) Need additional information in order to find the angle Ex pf 0.8 leading for V I 0 36.87 and pf 0.8 lagging for V I 0 36.87 Ex The transmission of electric power Time domain Power Factor (cont.) Frequency domain We will adjust the power factor by adding compensating impedance to the load. The objective is to minimize the power loss (i.e. absorbed) in the transmission line. R1 L1 R1 L1 The line Z LINE ( ) j j impedance 2 2 2 2 R1 j L1 Power Factor (cont.) The average power absorbed by the line is PLINE I m2 I m2 Re( Z LINE ) R1 2 2 The customer requires average power delivered to the load P at the load voltage Vm Solving for Im Vm I m P pf 2 2P Im Vm pf 2 PLINE P 2 R1 Vm pf max pf =1 Power Factor (cont.) compensating impedance A compensating impedance has been attached across the terminals of the customer’s load. pf 1 pfc cos c corrected The load impedance is Z R jX and the compensating impedance is ZC RC jX C We want ZC to absorb no average power so ZC jX C Power Factor (cont.) The impedance of the parallel combination ZP ZZC ZP RP jX P Z P P Z ZC The power factor of the new combination 1 X P pfc cos P cos tan RP Calculate for R and X P P ZZC ( R jX ) jX C ZP Z ZC ( R jX ) jX C RX C2 j R 2 X C ( X C X ) XX C R 2 ( X X C )2 RX C2 R 2 X C ( X C X ) XX C 2 j 2 R ( X XC ) R 2 ( X X C )2 Power Factor (cont.) X P R2 ( X C X ) X RP RX C 1 X P From pfc cos tan RP XP tan(cos 1 pfc) RP Solving for XC R2 X 2 XC R tan(cos1 pfc) X Typically the customer’s load is inductive ZC = capacitive j ZC jX C C 1 R2 X 2 C R tan(cos1 pfc) X Power Factor (cont.) Solving for C X R tan(cos1 pfc) C R2 X 2 R X 1 2 tan(cos pfc ) 2 R X R Let tan 1 X R R C 2 tan tan C 2 R X where cos1 pf and C cos1 pfc Example 11.6-1 I and pf = ? Load = 50 kW of heating (resistive) and motor 0.86 lagging pf Load 1 50 kW resistive load S1 P1 50 kW Load 2 motor 0.86 lagging pf 2 0 1 1 2 cos ( pf 2 ) cos (0.86) 30.7 P Q S2 S2 2 10030.7 86 j51 kVA Example 11.6-1 (cont.) S S1 S2 136 j51 145.220.6 kVA pf cos(20.6) 0.94 To calculate the current Vm I m S Vrms I rms 2 S I rms Vrms 145200 4 10 14.52 Arms Example 11.6-2 pf ==> 0.95, 1 C = ? 377 rad/s Z=100+j100 cos cos 45 0.707 pf lagging We wish to correct the pf to be pfc pfc 0.95 lagging R2 X 2 XC R tan(cos1 pfc) X 297.9 1 C 8.9 μF XC Example 11.6-2 (cont.) pfc 1 R2 X 2 XC R tan(cos1 pfc) X 200 1 C 13.3 μF XC Or use R C 2 tan tan C 2 R X C 13.3 μF The Power Superposition Principle i i1 i2 p i R (i1 i2 ) R (i i 2i1i2 ) R 2 2 2 1 2 2 1 T R T 2 2 P pdt (i1 i2 2i1i2 )dt T 0 T 0 R T 2 R T 2 2R T i1 dt i2 dt i1i2dt T 0 T 0 T 0 2R T 0 P1 P2 i1i2dt T 0 The Power Superposition Principle (cont.) 2R T i1i2dt 0 ? T 0 Let the radian frequency of the 1st source = m and the radian frequency of the 2nd source = n integer i I cos(m t ) 1 1 i2 I 2 cos(n t ) 2R T P12 i1i2dt T 0 2R T I1 I 2 cos(m t ) cos(n t )dt T 0 The Power Superposition Principle (cont.) 2 RI1 I 2 T P12 cos(m t ) cos(n t )dt 0 T 2 RI1 I 2 T (cos(( m n ) t ( )) cos(( m n ) t ( )))dt 0 T ;m n 0 RI1 I 2 cos( ) ;m n 2 For the case that m and n are not integer for example m = 1, n = 1.5 0 1 2t 1 2t P12 lim t pdt lim t 2 RI1I 2 cos t cos(1.5 t )dt t T t T 2 2 1 2t lim t 2 RI1 I 2 (cos0.5 t cos 2.5 t )dt 0 t T 2 The Power Superposition Principle (cont.) The superposition of average power The average power delivered to a circuit by several sinusoidal sources, acting together, is equal to the sum of the average power delivered to the circuit by each source acting alone, if and only if, no two of the source have the same frequency. If two or more sources are operating at the same frequency the principle of power superposition is not valid but the principle of superposition remains valid. For N sources I I1 I 2 I3 IN I m2 R P 2 Example 11.7-1 P=? (1) v A (t ) 12cos3t V and iB (t ) 2cos 4t A (2) v A (t ) 12cos 4t V and iB (t ) 2cos 4t A Example 11.7-1(cont.) Case I I1 ( ) 1.414 45 and I 2 ( ) 1.6 143 These phasors correspond to different frequencies and cannot be added. i1 (t ) 1.414cos(3t 45) and i2 (t ) 1.6cos(4t 143) Using the superposition i (t ) 1.414 cos(3t 45) 1.6cos(4t 143) The average power can be calculated as R T P (1.414 cos(3t 45) 1.6cos(4t 143)) 2 dt T 0 Since the two sinusoidal sources have different frequencies 1.4142 1.62 P P1 P2 6 6 13.7 W 2 2 Example 11.7-1(cont.) Case II I1 ( ) 1.2 53.1 and I 2 ( ) 1.6 143 Both phasors correspond to the same frequency and can be added. I ( ) 1.2 53.1+1.6 143 2.0 106.3 The sinusoidal current is i (t ) 2.0cos(4t 106.3) The average power can be calculated as 2.02 P 6 12 W 2 Power superposition cannot be used here because Both sources have same frequencies The Maximum Power Transfer Theorem Zt Rt jX t and ZL RL jX L Vt I ( Rt jX t ) ( RL jX L ) 2 2 m Vt RL I P RL 2 ( Rt RL )2 ( X t X L )2 We wish to maximize P set X L X t 2 Vt RL P 2 ( Rt RL ) dP For 0 we get RL Rt dRL Z L Rt jX t Z*t Maximum Power Transfer Coupled Inductors di1 di2 v1 L1 M dt dt di2 di1 v2 L2 M dt dt (a) both coil currents enter the dotted ends of the coils di1 di2 v1 L1 M dt dt di2 di1 v2 L2 M dt dt (b) one coil current enters the dotted end of the coil, but the other coil current enters the undotted end Summary Instantaneous Power and Average Power Effective Value of a Periodic Waveform Complex Power Power Factor The Power Superposition Principle The Maximum Power Transfer Theorem Coupled Inductor and Transformer