Download simple measurements

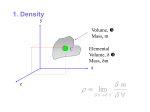
1. SIMPLE MEASUREMENTS
An objective of the first experiment in any first year physics lab is to give a student lots
of practice in making different kinds of measurements. In addition to measuring one
must learn how to estimate the uncertainties in reading the instruments one uses and to
calculate the uncertainties that accumulate in derived quantities. In this experiment the
actual activity is the study of a marble which is freefalling through a fluid. The final
result is the calculation of the property of a fluid called viscosity.
Theory
Basic and Derived Quantities
In physics, a quantity is described as being either
basic or derived. A derived quantity is one which
can be defined in terms of others, like speed
being distance divided by elapsed time. A basic
quantity is one which cannot be so defined. The
most obvious example is time.
Length
Length is a basic quantity being dependent only
on the unit that is used. You can measure a length
with a ruler, a vernier caliper or micrometer caliper and express the result in any unit you like, in
centimeters, or even in inches. The uncertainty in
reading the ruler is a reading uncertainty. You
can’t eliminate a reading uncertainty completely
but you can reduce its effect by measuring the
same thing a number of times and then taking an
average. You learned in the Orientation Workshop that the uncertainty in the average is the
standard deviation of the average. This statistical
number you have to calculate.
Area
Area is a derived quantity too. You can’t actually
measure an area because there is no instrument
for measuring one directly. But you can calculate
the area of a circle, for example, by first measuring its diameter and then using a formula. In the
same way the volume of an object is also a
derived quantity.
Mass
The mass of an object is a basic quantity whereas
weight is derived. These quantities are sometimes
confusing to the student because they are treated
as synonymous in everyday speech. But mass is a
measure of the amount of matter in a body, meaning atoms and molecules, and is therefore a fundamental quantity. Under everyday nonchemical
conditions, and nonrelativistic speeds, mass is constant. An astronaut has the same mass whether he
or she is floating in space or standing on the earth.
The unit of mass in the SI system of units is the
kilogram (kg). The mass of an object can be found
in terms of a standard mass in an experiment
involving accelerated motion.1
Weight
The weight of an object is the force of gravity on
the object and is therefore different from mass.
Unhappily, for purposes of understanding, the
magnitude of weight is found by “weighing” the
object with an instrument like a balance. But a
balance depends for its operation on gravity, and
therefore weight is a derived quantity.2 Weight is
a force expressed in newtons (abbreviated N). The
weight F g of an object of mass m where the
acceleration due to gravity is g is therefore 3
r
r
Fg = mg .
…[1]
Weight is therefore a derived quantity. At some
B1-1
1 Simple Measurements
place on the earth an object’s weight is constant
(independent of time) because neither the mass of
the object nor g change with time. But an object’s
weight will vary from one location to another over
the surface of the earth because the magnitude of
g varies slightly from place to place. More dramatically, the weight of an astronaut on the moon will
differ from his/her weight on earth. If an
astronaut is “floating” in space where the force of
gravity is zero his/her weight is zero. These facts
underline the derived nature of weight.
Density and Buoyancy
The density of an object is a simple scalar ratio—
the mass m of the object divided by its volume V.
It is commonly denoted ρ
ρ=
m
.
V
…[2]
Density, being dependent on mass and volume, is
a derived quantity and has no unit of its own; it is
commonly expressed in units kg.m–3.
A fluid’s density gives rise to its buoyancy.
One form of buoyancy is experienced by all of us
every day. If you place an object like a bar of soap
on the surface of water in a bathtub it will either
sink or float. If it sinks it is most often seen to
move downward through the water more slowly
than if released in air. It can be shown that if an
object is weighed in a fluid with a balance the
weight is less than the weight obtained in air. The
former is called the apparent weight, the latter the
actual weight. 4 This effect is buoyancy and is articulated by Archimides’ Principle: “The apparent
weight of an object is diminished by an amount
equal to the weight of the medium the object
displaces.” Clearly, a buoyant force acts in a direction opposite gravity and is directly proportional
to the density of the medium.
Why Study Fluids?
This experiment, besides providing lots of practice
in measuring things, involves the study of an
important property of a fluid. The study of fluid
behaviour is a large component of the environmental sciences. After all, our climate is driven by
the large-scale movement of water in rivers and
oceans. Rain is one fluid flowing through another
(air). Certain aspects of geology cannot be understood without knowing a little of the flow characteristics of molten rock. Also important is the topic
of an object moving down through a fluid as will
be studied here. This requires a little knowledge
of the physics of a freely falling body which we
consider next.
The Physics of a Body in Free Fall
The object you will actually study is a falling
sphere, a marble. The free body diagram of such
a sphere falling in a vacuum is drawn in Figure
1a. The sphere is subject to the force of gravity F g.
If the sphere should be falling in a medium like
air then the air will exert a frictional force, say F s,
on the sphere (Figure 1b). This force is in some
way dependent on the speed of the sphere, and
like all frictional forces, acts in a direction opposite
to the direction of motion. And finally, if the
B1-2
medium is of sufficient density then the sphere
may be subject to an appreciable buoyant force as
well, here represented in Figure 1c as F b. F b does
not depend on speed.
Calculating F b is easy; it is just the force exerted on the sphere by the mass of the medium the
sphere displaces (ala Archimedes’ Principle). The
calculation of F s is rather more difficult; it involves
the property of a fluid called viscosity, which we
consider next.
Simple Measurements 1
How Viscosity was Originally Defined
Viscosity was defined in the days of the Industrial
Revolution when oil began to be widely used as a
lubricant. From numerous experiments it was
found that a body which is pulled (or that falls)
through a fluid is subject to a resistive or damping
force which is not just a function of the body’s size,
but is also a function of the body’s speed and by
what could be termed the fluid’s “stickiness”. This
stickiness is a manifestation of the property called
viscosity. Viscosity was first modelled in terms of
the force exerted on a unit area of a flat plate
being pulled through a fluid (Figure 2). The force
per unit area on the plate was modelled as
proportional to the velocity gradient ∆v/∆d of the
fluid in the region adjacent to the plate, that is, the
force per unit area is given by
Fs
∆v
=η
,
A
∆d
where A is the plate’s cross-sectional area. The
proportionality factor η (pronounced “eta”) is the
viscosity. Viscosity is found to be a constant for a
pure liquid at constant temperature and in the SI
system has the unit Poiseuille (abbreviated Pl; 1 Pl
= 1 kg.m –1.s–1.) Viscosity (very definitely a derived quantity) is dependent on temperature; it
decreases as the temperature increases.
dependant
on speed
Fs
(b)
(a)
…[3]
Fs
Fb
(c)
v
mg
mg
mg
Figure 1. Freebody diagrams of a sphere moving downwards under the force of gravity: (a) in a vacuum, (b) in air
or a fluid which exerts a resistive force on the sphere, and (c) in a fluid whose density is sufficiently large to
produce an appreciable buoyant force in addition to a resistive force.
velocity vectors
of fluid "dragged"
along by the plate
d
v
v
Fs
Figure 2. A body moving through a fluid is subject to a resistive force which depends on the body’s velocity.
B1-3
1 Simple Measurements
Viscosity Derived in terms of a Falling Sphere
As you might imagine it is difficult to measure the
velocity gradient of a fluid in the neighbor-hood
of a moving plate, making eq[3] of limited use in
an actual experiment. A simpler model is a sphere
which is falling under gravity at its ter-minal
velocity as has already been sketched in Figure 1.
The magnitude of the resistive force on such a
sphere was found by the British mathemat-ician
and physicist G. G. Stokes (1819-1903) to have the
following form:
r
d r
Fs = –6πη  v ,
2
…[4]
where d is the sphere’s diameter and v its terminal velocity. (As shown in Figure 1, the –ve
sign in eq[4] arises because F s and v point in
opposite directions.)
In general, as the sphere falls, three forces are
exerted on it: the gravitational force F g, the buoyant force F b, and the resistive force F s. The gravitational force is given by
r 4  d 3 r
Fg = π   g ds ,
3 2
B1-4
…[5]
where ds is the density of the sphere. (F g and g
point in the same direction.) The buoyant force is
the force exerted by the mass of the displaced
fluid. Thus
r
4 d 3r
Fb = – π   g dl ,
3 2
…[6]
where dl is the density of the fluid. (F b and g point
in opposite directions.)
When the sphere is moving at its constant, or
terminal velocity, Newton’s First Law demands that
the sum of the forces on it be zero:
r r r
Fb + Fs + Fg = 0 .
…[7]
One can show that by substituting eqs[4], [5] and
[6] into eq[7] η has the following form
2
2g d
η =     (ds – dl ) ,
9v 2
…[8]
where g = g and v = v . Calculating η from the
measurement of v, d, ds and dl is the objective of
this experiment.
Simple Measurements 1
The Experiment
Exercise 0. Preparation
Orientation
Identify the large glass cylinder of shampoo
mounted on a stand. On the surface of the cylinder two marks are inscribed a distance 0.50 meter
apart to assist you in measuring average velocity.
Identify three marbles of different color and the
Prosonic model 1301 stopwatch (precision ± 0.01s).
The stopwatch will enable you to measure times of
fall between the marks. A vernier caliper has
been issued to enable you to measure the diameter of the marbles and therefore to calculate their
volumes. There are a number of measurements
both basic and derived in this experiment.
First Measurements
As you can see from eq[8] the expression for viscosity involves a number of factors. The simplest
measurements are the diameter d of the marbles
and their mass m. (The density of the shampoo is
given as 1.013 kg.l–1 @ 20ºC.) You can measure the
mass of the marbles with the balance set up in the
lab.
You will use the diameter of your marble in
two places—in eq[8] and in the density ρ (=m/V).
=AVERAGE(B2:B7)
=STDEV(B2:B7)/SQRT(6)
Average:
STDM:
You are strongly urged to measure a diameter
several times and take an average (as your marbles might not be as spherical as you expect). Your
table of data might resemble Figure 3. Find an
average ds for each marble and, of course, the
uncertainty in the average. For completeness note
the temperature of the shampoo.
First Uncertainties
Though you can estimate reading uncertainties,
uncertainties in derived quantities you have to
calculate. To get some practice in calculating uncertainties using the quadrature formula, first find
the uncertainty in density. You may wish to confirm your answer with the following result from
the Maple worksheet Quadrature Calculator:
the_error := 6
9
∆( d ) 2 m 2
2
π d8
+
∆( m ) 2
2
π d6
where ∆(d) represents the uncertainty in d, ∆(m)
the uncertainty in m.
Diameter (cm)
2.458
2.469
2.457
2.473
2.471
2.448
2.46266667
0.00402216
(2.463 ±0.004) cm
Figure 3. An example table (taken from an Excel spreadsheet) showing how you might tabulate the data for the
diameter of a marble and calculate the average and standard deviation of the mean (STDM).
B1-5
1 Simple Measurements
Exercise 1. Finding Terminal Velocity
The most dramatic activity in this experiment is
finding a marble’s terminal velocity. You may be
skeptical at first that a marble will indeed move
downwards through the shampoo at a uniform
velocity.
For the sake of an initial demonstration therefore, choose one of the marbles and very carefully
release it with the tweezers from a point just
beneath the surface of the fluid. (If you do this
carefully you should be able to minimize the
formation of bubbles which might otherwise
influence the marble’s motion.) As you watch the
marble descending, does it appear to be moving
at a constant velocity (or constant speed)? Do you
think the marble is probably moving at a constant
speed by the time it reaches the upper mark on
the cylinder? (There is more on this in the section
“Activities Using Maple”.) When the marble has
reached the bottom of the cylinder you can
retrieve it using the tool provided.
Go ahead and find the terminal speed v of
each marble by releasing it in the fluid and measuring its time of fall between the two marks. Take
several readings, tabulate your results and estimate the uncertainties.
Exercise 2. Calculating Viscosity
Now that you have averages for the factors v, ds , dl
and d for each marble you can calculate an η for
the use of each marble from eq[8]. Keep track of
your experimental uncertainties very carefully.
There is no “accepted value” for the viscosity of
this type of shampoo. The distributor suggests it
may be anywhere in the range 12 - 15 Pl.
?
?
?
Questions and Problems:
? Is there a systematic change in your calculated
value of viscosity as you go to larger marbles?
? What is your average value of viscosity?
What is the difference expressed as a percent
between your average value and, say, what
might be described as a “suggested average”
of 13.5 Pl?
List those quantities you have measured or
calculated in this experiment and describe
them as basic or derived.
The SI system of units is also described as the
MKSA system. What do the letters “M”, “K”,
“S”, “A” stand for? Comment on their nature
—are they basic or derived?
Exercise 3. Calculating the Uncertainty in the Viscosity
Calculating the experimental uncertainty in the viscosity is a good test of the method of quadratures.
You should be able to show that eq[8] is just a special example of Example 3 in Appendix 1, i.e., ∆η is
 ∆( r ) 2 g 2 r 2 ( ds −dl ) 2 ∆( ds ) 2 g 2 r 4 ∆( g ) 2 r 4 ( ds −dl ) 2

the_error := sqrt 4
+
+

9
2
2

v
v
v2
2
+
∆( dl ) 2 g 2 r 4
B1-6
v2
∆( v ) 2 g 2 r 4 ( ds −dl ) 2 
+

4
v

Simple Measurements 1
Having calculated the uncertainty in the viscosity, ∆η, can you state that your value of η agrees
with the “suggested average” value to within ∆η?
Physics Demonstrations on LaserDisc
from Chapter 31 Viscosity
Demo 14-02 Viscous Drag
Demo 14-06 Oil Viscosity
Activities Using Maple
T04Quadrature Calculator
Quadrature Calculator is a Maple worksheet that will calculate the uncertainty in any function based on
the variables you input. An alias to Quadrature Calculator is inside all experiment folders. To run just
double click its icon.
E01Simple Measurements
Simple Measurements is a Maple worksheet that enables you to model the motion of your marble to
determine if it really is moving with terminal velocity by the time it passes the top mark on the
cylinder of shampoo. An example of its output is shown in Figure 5.
B1-7
1 Simple Measurements
Figure 5. Typical Output from the Maple worksheet Simple Measurements.
SQ97
EndNotes for Simple Measurements
1
The mass obtained in such an experiment is called inertial mass.
Weighing an object with a balance is a process of comparing the gravitational force that is exerted on the object
with the force exerted on an object of known mass. (The latter is commonly referred to as a standard mass.) It only
works if gravity is present. A balance is usually not calibrated in force units like it should be but rather in mass units
of grams or kilograms. The mass obtained is often called the gravitational mass (for obvious reasons, perhaps, and to
distinguish it from the inertial mass which is found from an experiment involving accelerated motion).
3
The magnitude of g in Scarborough, rounded to 3 decimal places, is 9.804 m.s–2 . The vector nature of weight is
often ignored as the direction of the weight vector is usually understood to be downwards towards the center of the
earth.
4
In physics we try to avoid the word “actual” because it implies the existence of some intrinsic reality beyond what
is establishable by measurement. By “actual weight” here is only meant the weight measured in the absence of a
buoyant force, as might be obtained in a vacuum.
2
B1-8