Download Parallel Lines and Transversals

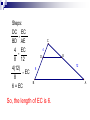
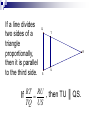
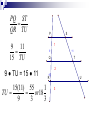
January 5, 2011
1)
2)
3)
Write your homework in your agenda:
Angle worksheet
Let’s practice constructing parallel and
perpendicular lines.
Then, let’s discuss angles and their
relationship to one another. Take out a
piece of paper to work out a few
problems.
Parallel Lines and
Transversals
The angle relationships that
are formed
What am I learning today?
Constructions
What will I do to show that I
learned it?
Determine the measurements of any
given angle created by the intersection
of parallel lines by a transversal
Parallel Lines and Transversals
What would you call two lines which do not intersect?
Parallel
B
A
D
C
The symbol || is used to
indicate parallel lines.
AB || CD
Parallel Lines and Transversals
A slash through the parallel symbol || indicates the
lines are not parallel.
B
AB || CD
A
D
C
Parallel Lines and Transversals
Transversal A transversal is a line which intersects two or
more lines in a plane. The intersected lines do
not have to be parallel.
j
k
m
t
Lines j, k, and m are
intersected by line t.
Therefore, line t is a
transversal of lines
j, k, and m.
Parallel Lines and Transversals
Identifying Angles -
j
1 3
2 4
k
5 7
6 8
t
Alternate
interior angles
___________________
are on the interior of
the two lines and on
opposite sides of the
transversal.
Alternate interior angles are:
3 and
or
6,
4 and
5
Parallel Lines and Transversals
Identifying Angles -
j
1 3
2 4
k
5 7
6 8
t
Alternate
exterior angles
___________________
are on the exterior of
the two lines and on
opposite sides of the
transversal.
Alternate exterior angles are:
1 and
or
8,
2 and
7
Parallel Lines and Transversals
Identifying Angles -
j
1 3
2 4
k
5 7
6 8
t
Corresponding angles
_____________________
are on the corresponding
side of the two lines and
on the same side of the
transversal.
Corresponding angles are:
1 and 5,
3 and 7,
2 and 6,
4 and
8
Parallel Lines and Transversals
Identifying Angles -
j
1 3
2 4
Vertical angles
_______________are
pairs of opposite
congruent angles formed
by intersecting lines.
k
5 7
6 8
t
Vertical angles are:
1 and 4,
2 and 3,
5 and 8,
6 and
7
Parallel Lines and Transversals
Identifying Angles -
j
1 3
2 4
Adjacent angles
_________________are
in the same plane and
share a common vertex
and a common side.
k
5 7
6 8
t
Adjacent angles are:
1 and 3,
2 and 4,
5 and 7,
6 and
8
Parallel Lines and Transversals
Identifying Angles – Check for Understanding
Determine if the statement is true or false. If false,
correct the statement.
1. Line r is a transversal
of lines p and q.
True – Line r intersects
4
3
both lines in a plane.
2
1
5
6
8 7
2.  2 and 10 are
alternate interior angles.
9 10
False - The angles are
11 12
16 15 14 13
corresponding angles on
transversal p.
Parallel Lines and Transversals
Identifying Angles – Check for Understanding
Determine if the statement is true or false. If false,
correct the statement.
3. 3 and  5 are
alternate interior angles.
1
2
8 7
3 4
6 5
9 10
11 12
16 15 14 13
False – The angles are
vertical angles created
by the intersection of q
and r.
4. 1 and 15 are
alternate exterior angles.
True - The angles are
alternate exterior angles
on transversal p.
Parallel Lines and Transversals
Identifying Angles – Check for Understanding
Determine if the statement is true or false. If false,
correct the statement.
5. 6 and  12 are
alternate interior angles.
1
2
8 7
True – The angles are
alternate interior angles
on transversal q.
3 4
6 5
6.
9 10
11 12
16 15 14 13
11 and 12 are
complementary interior
angles.
False – The angles are
supplementary.
Parallel Lines and Transversals
Identifying Angles – Check for Understanding
Determine if the statement is true or false. If false,
correct the statement.
7. 3 and 4 are
alternate exterior angles.
1
2
8 7
9 10
False – The angles are
supplementary.
3 4
6 5
11 12
16 15 14 13
8.
16 and 14 are
corresponding angles.
True – The angles are
corresponding on
transversal s.
EXAMPLE 1
Identify congruent angles
The measure of three of the numbered angles is 120°. Identify the
angles. Explain your reasoning.
SOLUTION
By the Corresponding Angles Postulate, m5 = 120°. Using the Vertical
Angles Congruence Theorem, m4 = 120°. Because  4 and  8 are
corresponding angles, by the Corresponding Angles Postulate, you
know that m 8 = 120°.
EXAMPLE 2
Use properties of parallel lines
ALGEBRA
Find the value of x.
SOLUTION

By the Vertical Angles Congruence Theorem, m 4 = 115°. Lines a
and b are parallel, so you can use the theorems about parallel lines.
m
4 + (x+5)°
= 180°
Consecutive Interior Angles Theorem
115° + (x+5)°
= 180°
Substitute 115° for m
x + 120 =
180
x = 60
4.
Combine like terms.
Subtract 120 from each side.
GUIDED PRACTICE
for Examples 1 and 2
Use the diagram at the right.
1.
If m
1 = 105°, find m
SOLUTION
m
4 = 105°
m
5 = 105°
m
8 = 105°
4, m
5, and m
8.
GUIDED PRACTICE
for Examples 1 and 2
Use the diagram at the right.
2. If m
3 = 68° and m
your steps.
8 = (2x + 4)°, what is the value of x? Show
GUIDED PRACTICE
for Examples 1 and 2
SOLUTION
m
7+m
8 = 180°
m
3= m
7
m
3 = 68°
68° + 2x + 4 =
72 + 2x =
180°
180°
2x = 108
x = 54
7 and
8 are supplementary.
Corresponding Angles
Substitute 68° for m
7 and (2x + 4)for m
Combine like terms.
Subtract 72 from each side.
Divide each side by 2.
8.
January 6, 2011
1)
2)
3)
Write your homework in your agenda:
Part Three: Problem Sets worksheet
Take out your homework and leave it on
your desk.
Here’s your Warm-Up….
WARM-UP…
Parallel Lines are cut by a transversal to create parking spaces.
Two angle measures are given. Determine the 8 angle
measures and label the diagram.
3x + 2 + 2x – 4 = 180
x = 36.4
111.2
68.8
111.2
2x - 4
68.8 degrees =
68.8
111.2
68.8
3x + 2 = 111.2 degrees
What am I learning today?
Triangle Proportionality Theorem
What will I do to show that I
learned it?
Use proportionality theorems to
determine segment length
If a line parallel to
one side of a
Q
triangle intersects
the other two sides,
then it divides the
two side
S
proportionally.
T
R
U
RT RU

If TU ║ QS, then TQ US
Finding the length of a segment

AB ║ ED, BD = 8, DC = 4, and AE = 12.
What is the length of EC?
C
4
D
8
B
E
12
A
Steps:
DC EC
=
BD AE
4 = EC
8 12
4(12)
= EC
8
6 = EC
C
4
D
8
B
So, the length of EC is 6.
E
12
A
QUESTION
What is the
Triangle
Proportionality
Theorem?
If a line divides
two sides of a
triangle
proportionally,
then it is parallel
to the third side.
Q
T
R
S
U
RT
RU
, then TU ║ QS.
If

TQ US
Determining Parallels

Given the diagram, determine whether
MN ║ GH.
LM
G
56
=
MG
8
=
21
3
21
M
LN
NH
56
=
48
16
8
L
N
48
16
H
=
3
3
1
≠
3
1
MN is not parallel to GH.
QUESTION
What is the Converse
of the Triangle
Proportionality
Theorem?
 If
three parallel lines intersect two
transversals, then they divide the
transversals proportionally.
 If r ║ s and s║ t and l and m
intersect, r, s, and t, then UW VX
r
U
WY
t
s
W
Y
m
V
X
Z

XZ
Using Proportionality Theorems
the diagram 1
 2  3, and
PQ = 9, QR = 15,
and ST = 11.
What is the length
of TU?
 In
P
S
1
9
11
Q
T
2
15
R
U
3
PQ ST

QR TU
9
11

15 TU
9 ● TU = 15 ● 11
15(11) 55
1
TU 
 or18
9
3
3
P
S
1
9
11
Q
T
2
15
R
U
3
QUESTION
What is the
Proportionality
Theorem for Parallel
Lines?
EXAMPLE 1
Find the length of a segment
In the diagram, QS || UT , RS = 4, ST = 6, and QU = 9. What is the length of
RQ ?
SOLUTION
RQ
QU
=
RQ
=
9
RQ = 6
RS
ST
Triangle Proportionality Theorem
4
6
Substitute.
Multiply each side by 9 and simplify.
GUIDED PRACTICE
1.
Find the length of YZ .
SOLUTION
XW
WV
44
35
=
XY
YZ
Triangle Proportionality Theorem
=
36
YZ
Substitute.
315
11
Simplify
YZ =
ANSWER
So length of YZ =
315
11
GUIDED PRACTICE
2. Determine whether PS || QR .
SOLUTION
PQ
PN
=
50
90
=
RS
SN
5
9
=
40
72
ANSWER
So Because =
PS is parallel to QR
PQ
PN
=
RS
SN
PS || QR ,
=
5
9