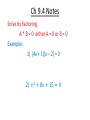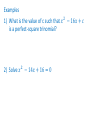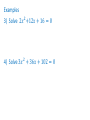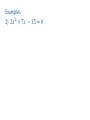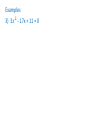* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ch 9
Linear algebra wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Signal-flow graph wikipedia , lookup
Cubic function wikipedia , lookup
Factorization wikipedia , lookup
System of polynomial equations wikipedia , lookup
System of linear equations wikipedia , lookup
Quartic function wikipedia , lookup
Elementary algebra wikipedia , lookup
History of algebra wikipedia , lookup
Chapter 9.1 & 9.2 Common Core – F.IF.7.a, A.CED.2, F.IF.4, F.IF.5, F.IF.8a, F.IF.9, & F.BF.3 Graph linear and quadratic functions and show intercepts, maxima, and minima. Objective – To graph quadratic functions of the form y = ax2, y = ax2 + c and y = ax2 + bx +c . Ch 9.1 – 9.2 Notes Quadratic Graphs y = a𝑥 2 + bx + c If a is positive it cups up If a is negative it cups down To find the vertex −𝑏 ( 2𝑎 , plug it in) Axis of symmetry x = the x-coordinate of the vertex If you factor the quadratic it will tell you were you cross the x-axis. Chapter 9.1 Solving Quadratic Equations When you solve the Quadratic it tells you where you cross the x-axis. 1) x = 2 & x = 3 (Crosses the x-axis in 2 places) 2) x = -4 & x = -4 (Crosses the x-axis in 1 place) 3) Not factorable (Doesn’t cross the x-axis) Chapter 9.3 Common Core – A.REI.4.b, N.Q.2, A.APR.3, A.CED.1, & A.CED.4 Solve quadratic equations by inspection, taking square roots. Objective – To solve quadratic equations by graphing and using square roots. Ch 9.3 Notes Solving Quadratic Equations When you solve the Quadratic it tells you where you cross the x-axis. 1) x = 2 & x = 3 (Crosses the x-axis in 2 places) 2) x = -4 & x = -4 (Crosses the x-axis in 1 place) 3) Not factorable (Doesn’t cross the x-axis) Chapter 9.4 Common Core – A.REI.4.b, A.SSE.3.a, A.CED.1, & A.F.IF.8a Solve quadratic equations by factoring. Objective – To solve quadratic equations by factoring. Ch 9.4 Notes Solve by Factoring A * B = 0 either A = 0 or B = 0 Examples 1) (4x + 1)(x – 2) = 0 2) 𝑥 2 + 8𝑥 + 15 = 0 Examples 3) 4𝑥 2 - 21x = 18 4) You are constructing a frame for a 17 inch by 11 inch photo. You want the frame to be the same width all the way around and the total area of the frame and photo to be 315 𝑖𝑛2 . What is the outer dimensions of the frame? Chapter 9.5 Common Core – A.REI.4.a, N.Q.3, A.SSE.1.a, A.SSE.1.b, A.SSE.3.b., A.CED.1, A.REI.1, A.REI.4.b, & A.F.IF.8a Use the method of completing the square to transform any quadratic equation in s into an equation of the form (x – p)2 = q Objective – To solve quadratic equations by completing the square. Ch 9.5 Notes Completing the Square 1) Make sure the leading coefficient is equal to 1 (a = 1) 2) Move the constant term c to the right of the equal sign. (move c.) 3) Take b and divide by two, square it and add it 𝑏 2 to both sides of the equation. ( ) 2 4) Factor and Solve the Equation Examples 1) What is the value of c such that 𝑥 2 − 16𝑥 + 𝑐 is a perfect-square trinomial? 2) Solve 𝑥 2 − 14𝑥 + 16 = 0 Examples 3) Solve 2𝑥 2 +12𝑥 + 16 = 0 4) Solve 3𝑥 2 + 36𝑥 + 102 = 0 Chapter 9.6 Common Core – A.REI.4.a, N.Q.3, A.CED.1, & A.REI.4.b Use the method of completing the square to transform any quadratic equation in s into an equation of the form (x – p)2 = q… Derive the quadratic formula from this form. Objectives – To solve quadratic equations by using the quadratic formula. To find the number of solutions of a quadratic equation. Ch 9.6 Notes Quadratic Formula a𝑥 2 + 𝑏𝑥 + 𝑐 = 0 x= Example 1) 𝑥 2 - 8 = 2x −𝑏± 𝑏2 −4𝑎𝑐 2𝑎 Examples 2) 2𝑥 2 + 7𝑥 − 15 = 0 Examples 3) 3𝑥 2 - 17x + 11 = 0 a𝑥 2 + 𝑏𝑥 + 𝑐 = 0 x= −𝑏± 𝑏2 −4𝑎𝑐 2𝑎 𝑏 2 - 4ac is called the discriminate 𝑏 2 - 4ac > 0 (There are 2 real solutions) 𝑏 2 - 4ac = 0 (There is 1 real solutions) 𝑏 2 - 4ac < 0 (There is no solution) Find the number of real-number solutions of each equation. 1) 3𝑥 2 − 6𝑥 + 9 = 0 2) 2𝑥 2 − 15 = 0 3) 4𝑥 2 − 20𝑥 + 25 = 0 Chapter 9.7 Common Core – F.LE.a, F.IF.4, F.LE.2, F.LE.3 & S.ID.6a Prove that linear functions grow by equal differences…and that exponential functions grow by equal factors over equal intervals. Objective – To choose a linear, quadratic, or exponential model for data. Ch 9.7 Notes Linear, Quadratic, Exponential Models y = mx + b (Linear) y = a𝑥 2 + bx + c (Quadratic) y = a * 𝑏 𝑥 (Exponential)