* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download (buoyancy-driven) stack ventilation
Computational fluid dynamics wikipedia , lookup
Compressible flow wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Fan (machine) wikipedia , lookup
Fluid thread breakup wikipedia , lookup
Aerodynamics wikipedia , lookup
Reynolds number wikipedia , lookup
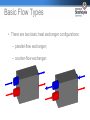
Ventilation for Low Energy Buildings Dr Nick Kelly Energy Systems Research Unit (ESRU) Mechanical Engineering University of Strathclyde Overview • Ventilation and Infiltration • Natural Ventilation – wind-driven pressure – buoyancy-driven flow • Mechanical Ventilation – fans – system resistance – operating conditions – heat recovery (heat exchangers) Ventilation and Infiltration • all buildings require some form of ventilation – supply of fresh air (comfort) –for removal or dilution of contaminants (health) • ventilation is the deliberate supply of air to a building – natural ventilation – using a fan and ductwork • infiltration is the unwanted leakage of air onto a building through cracks and apertures in the building fabric Measuring Infiltration • measurement of air leakage [infiltration] in buildings is done using a blower door test • the building is pressurised to 50Pa and the decay rate of pressure measured to get a leakage rate • … this can be divided by 20 to get the typical infiltration under normal conditions • some typical infiltration levels are: > 1.5 (leaky [older house]) < 1.5 – 0.5 (average) < 0.5 (low leakage) 0.03 (PassivHaus) Natural Ventilation • is the ventilation type in most smaller UK buildings • driven by wind pressure and density variations (buoyancy) – single sided ventilation (buoyancy-driven) – stack ventilation (buoyancydriven) – cross flow ventilation (wind driven) Natural Ventilation • driving force will often be a combination of wind + density (buoyancy) forces • influenced by: – wind direction – wind speed – ventilation opening location – interior/exterior temp. difference – internal gains – building geometry • no energy required for ventilation • but results in highly variable flow (magnitude and direction) Buoyancy Driven Flow • from the Gas Laws (PV=mRT); air density 1/T • The weight of two vertical columns of air at different temperatures separated by a vertical surface will differ and a pressure difference, Ps, will be created across the intervening surface. If openings exist in this surface, Ps will cause a flow of air to occur. Pa P gz Ra 1 1 T1 T2 1 1 P 3462 z T1 T2 Buoyancy Driven Flow • The pressure gradients in the two columns will differ, the greater of the gradients occurring where the temperature has the lower value. Tint Text Ph2 Height h2 neutral plane Ph1 h1 external pressure internal pressure gradient Pressure Buoyancy Driven Flow • The total induced stack effect pressure is: Ps = Ph1 + Ph2 1 1 1 1 Ps 3462h2 3462h1 Text Tint Text Tint 1 1 Ps 3462h2 h1 Text Tint Wind Induced Pressure • when wind blows over a building it creates regions of either positive or negative (below atmospheric pressure) • these can be used to promote flow Wind Induced Pressure • the generated pressure on a surface is can be approximated using: 1 2 Pi ,d Cid U d 2 • Ci,d is a pressure coefficient for a surface at some angle i in relation to the wind direction d • the coefficient is generally positive for surfaces facing the wind and negative for leeward surfaces • lists of ‘typical’ coefficients are tabulated for different surface types at 22.5o intervals • alternatively, Cp values can be taken from C FD models or wind tunnel tests Flow Through Fabric • wind-induced flow can occur deliberately (open window) or be unintentional – though cracks and other small openings • typically the flow rate through the opening is expressed as a function of the pressure difference across it m f ( P ) • e.g. power law flow n m a P Flow Through Fabric Natural Ventilation • given the range of driving forces and general complexity of natural ventilation (strongly coupled with temperatures) computer modelling is often used to assess natural ventilation schemes • gives an indication of the variability of flow and the influence on internal temperatures, comfort and air quality Natural Ventilation the reality! the drawing … Mechanical Ventilation • ventilating a building mechanically requires one or more fans and a distribution system Fan Performance • in mechanical ventilation systems fans can be used to move large volumes of air from one point to another • the pressure and resulting flow generated by a fan is an order of magnitude greater than that achievable from either buoyancy or wind induced pressure 2 m m m P ao a1 a2 a3 P • the flow induced by a fan is typically expressed as a 3rd order function m/ 3 Ducting Pressure Losses • the job of the distribution system is merely to convey air from one point to another • the fan is required to overcome various frictional losses in the system; there are proportional to the air velocity2 P V2 pL K 2 4 fL V 2 pL D 2 • these losses occur: - at the interface of the air and the ducting - at fittings (junctions, expansions, etc) - due to equipment (heating/cooling coils, etc) m/ System Flow Rate • the flow rate achieved by a particular fan is determined by identifying the intersect of the fan performance and system resistance P m/ Fan Laws • the so-called fan laws can also be applied to assess the effect of changes in fan speed • volume flow (m3/s) varies proportionally to the fan speed Q 2 N 2 Q1 N1 • Pressure (Pa) varies as the square of the fan speed P2 N 2 P1 N1 2 • power consumed (W) varies as the cube of the fan speed p2 N 2 p1 N1 2 MVHR • modern low energy buildings are typically tightly sealed and employ mechanical ventilation heat recovery rather than relying on natural ventilation • this gives a consistent supply of fresh air, without a significant heating energy penalty • heat recovery in an MVHR system is typically achieved using a plate heat exchanger • this takes heat from the warm exhaust stream and transfers it to the incoming Exchanger Basics • As the name implies a heat exchanger is a device that promotes the transfer of heat between two or more fluids. • Heat exchange can take place due to: – mixing of the fluids; – heat flow between fluids separated by a solid surface (no mixing can take place). hot fluid into heat exchanger at temperature T1 cold fluid exits heat exchanger at temperature T4 heat exchange from hot to cold. hot fluid exits heat exchanger at temperature T2 cold fluid enters heat exchanger at temperature T3 Consider the simple heat exchanger shown above: as a "warm" fluid passes over the exchanging surface it losses heat; this heat is absorbed by the "cold" fluid, which is in contact with the reverse side of the heat exchanging surface. Energy Analysis • Heat exchangers can be analysed using the steady flow energy equation (SFEE). heat transfer with surroundings – work = output energy rate – input energy rate Simplifies to: Energy Analysis • For a simple two stream heat exchanger the energy balance is: If Then the equation becomes heat lost from hot stream = heat gained by cold stream Basic Flow Types • There are two basic heat exchanger configurations: – parallel-flow exchanger; – counter-flow exchanger. Parallel Flow • • In a parallel-flow exchanger, the fluid inlet ports of the two air streams are located at the same end of the exchanger. The stream-to-stream temperature difference is the greatest at the inlet and at it’s smallest at the outlet. Hot fluid outlet 2 Hot fluid inlet 1 Cold fluid inlet 3 Cold fluid outlet 4 1 Temp. T Hot fluid temp. 2 4 • The greatest heat transfer between the streams occurs at the inlet. Cold fluid temp. 3 Length Counter Flow • • In a counter-flow exchanger, the fluid inlets are located at opposite ends of the exchanger results in a near constant temperature difference throughout the length of the exchanger Hot fluid outlet 2 Hot fluid inlet 1 Cold fluid outlet 4 Cold fluid inlet 3 1 Temp. T Hot fluid temp. • near constant heat exchange per unit length. 2 4 Cold fluid temp. 3 Length Efficiency • In any heat exchange process the efficiency can be defined as: The primary stream is the stream in the heat exchanger that gets the “useful” effect of the heat transfer: the stream being heated or cooled. The secondary stream performs the useful effect, removing heat from or giving up excess heat to the primary stream. Efficiency • By this definition of efficiency equation (5) would give us an ideal efficiency of 100%! Hot fluid outlet 2 Hot fluid inlet 1 Cold fluid outlet 4 Cold fluid inlet 3 Qloss A more realistic form of equation 5 is therefore: Effectiveness • A useful measure of a heat exchanger’s ability to transfer heat is its effectiveness. • The maximum theoretical energy transfer occurs when the cold fluid exits at the inlet temperature of the warm fluid. • The fluid with the smallest heat capacity, (W/K), will experience the largest temperature rise and the maximum amount of heat transfer is dictated by the maximum amount of heat which this fluid can lose or pick up. Effectiveness • The maximum possible heat transfer is therefore: The effectiveness for a cold primary stream (fluid being heated) is: Hot fluid outlet 2 Hot fluid inlet 1 Cold fluid outlet 4 Cold fluid inlet 3 Qloss Effectiveness Similarly, the effectiveness for a warm primary stream (fluid being cooled) is: Hot fluid outlet 2 Hot fluid inlet 1 Cold fluid outlet 4 Cold fluid inlet 3 Qloss It is important to recognize the correct primary stream to get a correct value of effectiveness! Common Heat Exchangers • • • a common heat exchanger in ventilation systems is the plate heat exchanger used for transferring heat between two gases or two liquids used extensively in buildings for ventilation heat recovery Common Heat Exchangers • • • • finned tube heat exchangers are used to transfer heat between a fluid and a gas the fluid flows inside the tubes the gas flows over the fins heat is transferred much more readily to and from a fluid than to and from a gas the fins act to greatly increase the heat transfer to the gas