Download Blackbody Radiation

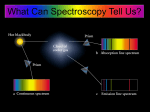
Blackbody Radiation
Blackbody Radiation
Blackbody = something that absorbs all electromagnetic radiation incident on
it.
A blackbodyy does not necessarilyy look black.
Its color depends on its temperature.
The Sun and other stars behave
approximately like blackbodies.
The amount of electromagnetic radiation, with a given wavelength, emitted by a
square meter
t off a blackbody’s
bl kb d ’ surface
f
iin one second
d iis given
i
bby th
the Pl
Planckk blackbody
bl kb d
radiation law. It is displayed as a graph on the following slide.
The temperature scale used by physicists and astronomers is the absolute Kelvin scale.
The temperature at which a body can emit no energy is absolute zero. One Kelvin = 1
Celsius degree = 1.8 Fahrenheit degree. The freezing point of water is about 273 K =
32oF.
1
flux in watts per square m
meter
Comparison of the Solar (T = 5800 K)
Continuous Spectrum with that of a 3500 K Star
wavelength in nanometers
The 3500 K star is brightest at a wavelength around 828 nm. This is infrared
radiation, so we don’t see it. Since the visible part of this star’s spectrum is
strongest at red and orange wavelengths, it has a faint red - orange color.
flux in watts per square meter
Planck’s Law for Blackbody Radiation
For a star with T = 7500 K
For a star with T = 5800 K
The visible spectrum
(about 400 to 700 nm)
is superimposed on the
graph).
wavelength in nanometers
The peak of the graph for the star with a surface temperature of 7500 K is at a
wavelength of 386 nm (violet). In the visible light from this star, there would be a
bit more blue and violet than the other colors. The star would have a faint blue
color.
Our sun has a surface temperature of 5800 K. The wavelength at which it is brightest
is 500 nm (green). It has a faint yellow color.
2
Wien’s Law and the Stefan-Boltzman Law
7000 K
Notice that (a) the higher the temperature, the
shorter the wavelength at which the star is
brightest and (b) the higher the temperature
the greater the area under the graph.
5800 K
F
3500 K
(a) is Wien’s law. Stated more precisely, it
says that the wavelength λmax at which the
blackbody is brightest is inversely
proportional to its absolute temperature T. If
T is in Kelvins and λ is in nm, then
λ=
2.898 × 106
T
(b) is the Stefan-Boltzman Law: The energy radiated in one second by one
square meter of the blackbody’s surface (E) is directly proportional to the fourth
power of its temperature. If E is in watts per square meter and T is in Kelvins,
4
E = σT 4
or
E A ⎛ TA ⎞
=⎜ ⎟ .
E B ⎝ TB ⎠
σ is a constant whose value we won’t need
because we’ll always use the second form of the
Stefan-Boltzman law.
Example 1: The surface temperature of the Sun is about 5800 K, and the surface
temperature of Sirius is about 11,000 K. Compare the surface flux (the
electromagnetic energy emitted by 1 m2 of surface in 1 second) of the star Sirius
with the surface flux of the Sun.
A = Sirius and B = Sun
FA ⎛ 11000 ⎞
=⎜
⎟
FB ⎝ 5800 ⎠
4
TA = 11,000 K
FA
4
= (1.897 )
FB
TB = 5800 K
FA
= 12.9
FB
Sirius is about 13 times
brighter than the sun.
Example 2: At what wavelength does Sirius emit the most electromagnetic
energy?
λ=
2.898 × 106
.
T
T = 11,000 K
λ=
2.898 × 106
.
11000
λ = 263 nm
This is a bit shorter than violet, so Sirius is brightest at ultraviolet wavelengths.
The visible wavelengths at which it is brightest are violet and blue, so Sirius has
a pale blue color.
3
Atoms
•
•
•
•
•
•
•
A neutral atom consists of a nucleus, made of protons and neutrons, and
enough electrons to neutralize the positive charge of the protons.
The diameter of the nucleus is about 1 femtometer (1 fm = 10-15m).
m)
The “cloud” of electrons, on the other hand, occupies a volume with a
diameter of about 0.1 nm (1 nm = 10-9 m).
Since mp = 1836 me and mn = 1839 me, most of the mass of an atom is
concentrated in its nucleus.
An ion is an atom that has either a deficit or a surplus of electrons.
The process of removing an electron from an atom is called “ionization”.
The number of protons in the nucleus determines the chemical identity of the
atom.
The Bohr Model of the Hydrogen Atom
n=3
n=2
The electron in a hydrogen atom moves in a
circular orbit. The radius can only have one of
a set of discrete values, rn (n = 1, 2, 3, …).
n = 1,
1 the
th lowest
l
t possible
ibl orbit,
bit is
i called
ll d the
th
ground state of the atom. The states above the
ground state are called excited states.
n=1
The electron can transfer to a higher orbit if it
absorbs a photon of energy equal to the energy
difference between the two orbits.
When an electron transfers to a lower orbit, it
emits a photon with energy equal to the energy
difference between the two orbits.
A transfer from one orbit to another is called a
transition.
4
An energy level diagram is a graphical representation of the energies that are
available to the electron in the atom. The following is an energy level diagram for the
hydrogen atom.
Paschen Series - infrared
n=5
n=4
n=3
Balmer Series - visible
n=2
α β γ
Lyman Series - ultraviolet
n=1
Any atom can be described in terms of its
energy levels. He, for example, has twice as
many protons as H. Its energy levels are closer
together, and the ionization potential for
removing one electron from a neutral He atom
in its ground state is 24.5 eV.
The higher energy levels are
increasingly close together and
blend into the continuum at an
energy of 13.6 eV above the
ground state. When a hydrogen
atom absorbs a photon with
energy greater than or equal to
13.6 eV, the electron is removed
from the atom. 13.6 eV is the
ionization potential of the
hydrogen atom.
λ Hα = 656.3nm
λ Hβ = 486.1nm
λ Hχ = 434.0nm
Kirchoff’s Rules
I. A solid, liquid, or dense gas has a continuous spectrum.
II. A hot, low-density gas has an emission (bright line) spectrum.
III. When light with a continuous spectrum passes through a cool gas, the result is an
absorption spectrum.
The dominant component of a star’s spectrum is a set of absorption lines. The visible lines
in the absorption spectrum of the Sun are shown below.
5
3000 K
4500 K
5500 K
7500 K
10,000 K
20,000 K
40,000 K
Dependence of Stellar Spectra on Temperature
(Spectral Classification)
Spectral Classes
Type
Hydrogen
Balmer
Line
Strength
Approximate
Surface
Temperature
Main Characteristics
Examples
Singly ionized helium lines either in
emission or absorption. Strong
ultraviolet continuum.
10 Lacertra
11,000 - 25,000
Neutral helium lines in absorption.
Rigel
Spica
Strong
7,500 - 11,000
Hydrogen lines at maximum strength for A0
stars, decreasing thereafter.
Sirius
Vega
F
Medium
6,000 - 7,500
Metallic lines become noticeable.
Canopus
Procyon
G
Weak
5,000 - 6,000
Solar-type spectra. Absorption lines of
neutral metallic atoms and ions (e.g.
once-ionized calcium) grow in strength.
Sun
Capella
K
Very
Weak
3,500 - 5,000
Metallic lines dominate. Weak blue
continuum.
Arcturus
Aldebaran
M
Very
Weak
< 3,500
Molecular bands of titanium oxide
noticeable.
Betelgeuse
O
Weak
> 25,000 K
B
Medium
A
6
7
The Luminosity Effect
From “An Atlas of Stellar Spectra” by Morgan, Keenan, and Kellman
•
•
•
•
•
In a dense stellar atmosphere, the atoms collide more frequently than in a low
density stellar atmosphere.
The collisions broaden the absorption lines in the star’s spectrum.
spectrum
Giant stars are larger and less dense than main sequence stars, so their
absorption lines are narrower than those of main sequence stars.
The spectra shown above illustrate this effect. Notice that the absorption lines
in the spectra of the giant (13 Mono ) and supergiant (HR 1040) stars are
narrower than the absorption lines in the main sequence star α Lyrae.
This enables us to use the star’s spectrum to determine its luminosity as well
as its temperature.
8
T = 50,000 K
T = 27,000 K
9
T = 11,000 K
T = 7200 K
10
T = 6000 K
T = 5100 K
11
T = 3700 K
Composition of the Sun
Element
Hydrogen
% by Number
of Atoms
91 0
91.0
% by Mass
70 9
70.9
Helium
8.9
27.4
Carbon
0.03
0.3
Nitrogen
0.008
0.1
Oxygen
0.07
0.8
Neon
0.01
0.2
Magnesium
0.003
0.06
Silicon
0.003
0.07
Sulfur
0.002
0.04
Iron
0.003
0.1
12
The Doppler Effect
Vr
Vr
V
Vt
Vt
Doppler Simulation
V
Vr < 0
Vr λ observed − λ lab
=
c
λ lab
Vr = radial velocity
Vr > 0
Vt = tangential velocity
Example: The laboratory wavelength of the blue-green line in the hydrogen spectrum is
486.1 nm. If the wavelength of this line in the spectrum of a star is 485.9 nm, what is the
d ve
velocity
oc y of
o thee star?
s
radial
λ lab = 486.1 nm,
Vr = c
λ observed − λ lab
λ lab
λ observed = 485.9 nm,
c = 3.00 × 108 m / s
m ⎞ 485.9 − 486.1
⎛
= ⎜ 3.00 × 108 ⎟
= −1.2 × 105 m / s = −1.2 × 102 km / s
s ⎠
486.1
⎝
13