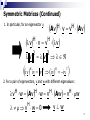Download Eigenvectors

Tutorial 6.
Eigenvalues &
Eigenvectors.
1. Reminder: Eigenvectors
A vector x invariant up to a scaling by λ to a multiplication by
matrix A is called an eigenvector of A with eigenvalue λ :
A x  x
The eigenvectors can be found via:
A x  x 
A x  I x 
A  Ix  0
This equation a has nontrivial (nonzero) solutions only for λ
satisfying:
det A  I   0
2
Reminder (continued)
det A  I   0
•
For an n-by-n matrix, this is a polynomial of order n.
•
It is known as the characteristic polynomial.
•
This poynomial has exactly n roots (possibly with multiplicities) λ1, …,
λn. The eigenvector xj , corresponding to λj, is found via solution of
A   jI x j  0
3
Symmetric Matrices - Theorem
Let A be a symmetric real n-by-n matrix. then:
1. All the eigenvalues are real λ1, …, λn.
2. Eigenvectors with different eigenvalues are orthogonal.
3. There is an orthonormal basis consisting of eigenvectors of A.
Proof
First, let us note that
Indeed,
Av 
 w  v  Aw
H
v H  A w  
n
n
n
j 1
k 1
i,k 1
 v j  a jk wk   v ja jk wk
a jk  akj 

H
n

akj v j w k  A v H  w
i,k 1
4
Symmetric Matrices (Continued)
Av   v  v  Av 
H
H
 v   v  v   v 
H
1. In particular, for an eigenvector v,
v
2
v
iv iv  v
H
2
2
H
 
 i v   i v
H
T

2. For a pair of eigenvectors, v and w with different eigenvalues:
v  w  A v   w  v  Aw  v  w
H
H
    vH  w  0
H
H
vw
5
Symmetric Matrices (Continued)
3. (There is an orthonormal basis consisting of eigenvectors of A)
For the case d=1, the proof is trivial. We proceed by induction.
Consider the general case d=n>1. The matrix A has at least one
eigenvalue (solution, possibly multiple of characteristic equation) for
which we have an eigenvector, and it is real due to (1). Let v1 be the
associated eigenvector. Let
V   {w  n v1H  w  0}
The dimension of V  is n-1, and for a vector w from it, the
transformation by A keeps it within V  :
v1H  A w   A v1 H  w  1 v1H  w  0
6
Symmetric Matrices (Continued)
(3) In the subspace V  an orthonormal basis y1,…yn-1 can be constructed.
The linear transformation produced by A in V  is described by a n-1·n-1
matrix B in the basis of y1,…yn-1.
Consider the n·n-1 matrix Y, describing the transition from coordinates
y1,…yn-1, to x1,…xn. Then, B=YTAY, and therefore B is symmetric, and real.
Therefore, B has at least one eigenvector, vB. Then for this eigenvector:
Bv B   B v B  YT AY v B   B v B  AY v B   BY v B
We have shown that YvB is another eigenvector of A, orthogonal to v1.
From here the proof continue by induction via d=n-2 to d=1.
7
Spectral Factorization
In the basis of eigenvectors of matrix A, the action of A on arbitrary
vector x is very simple:



 
A x  A v1H  x v1    v1H  x v n  c11 v1  ...  c nn v n
Now, consider an action of orthonormal
 v H
1

matrix Q, built of eigenvectors of A, on QH x  

 v H
an arbitrary vector x:
n

Therefore,
|  1  0   v1T
|



H
QΛ Q x   v1  v n       

 |
|   0  n   v nT

 
 
vH  x 


 1 
x    
vH  x 

 n 



x 


 1 v1H x v1  ...  n v H
n x vn
8
Spectral Factorization (continued)
Since for any vector x,
QΛ QH x  A x  QΛ QH  A
Example: Perform a spectral factorization of the following matrix:
 3  1  1


A   1 2
0
 1 0
2 
First, let’s find the eigenvalues of A:
1 
3    1


det   1 2  
0   3   2   2   1 12      12    
  1
0
2   


 2   3   2     1  1  2    2  5  4  0
9
Spectral Factorization (continued)
First, let’s find the eigenvalues of A:
2   2  5  4   0
1  2
5  25  16
 2,3 
 4 ,1
2
Now we can find corresponding eigenvectors:
 1  1  1



1
0
0

 x1  0
 1 0
0 

x1  0 1 / 2
1 / 2

T
10
Spectral Factorization (continued)
 1  1  1 



1

2
0

x2  0
 1 0  2
 1  1  1


0

1
1

x2  0
 0
1  1
 1  1  1


0

1
1

x2  0
 0
0
0 
x 2  1 / 6  2 1 1T
 2  1  1



1
1
0

x3  0
 1 0
1 
1 
2  1


0
1
/
2

1
/
2

x3  0
0  1 / 2 1 / 2 
1 
2  1


0
1
/
2

1
/
2

x3  0
0 0
0 
x 3  1 / 3 1 1 1T
11
Spectral Factorization (continued)
|

Q   v1
 |
A  QQ T
 3 1

  1 2
 1 0
|
v2
|
 2 / 6

  1/ 6
 1/ 6

 1

0
2 
|   2 / 6
 
v3    1 / 6
|   1 / 6

1 / 3

1 / 2 1 / 3
1 / 2 1 / 3

0
1 / 3  4 0 0   2 / 6 1 / 6


1 / 2 1 / 3  0 2 0   0
1/ 2
 1 / 2 1 / 3  0 0 1   1 / 3 1 / 3


0
1/ 6 

1/ 2
1/ 3 

12