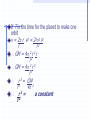Download Summary Presentation, Topic 9.4 File

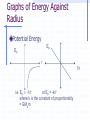
Mechanics
AHL 9.4 Orbital Motion
Orbital Motion
Gravitation provides the centripetal force for
circular orbital motion
The behaviour of the solar system is
summarised by Kepler´s laws
Kepler´s laws state


1. Each planet moves in an ellipse which has the
sun at one focus
2. The line joining the sun to the moving planet
sweeps out equal areas in equal times
Deriving the Third Law
Suppose a planet of mass m moves with
speed v in a circle of radius r round the
sun of mass M
The gravitational attraction of the sun for
the planet is = G Mm
r2
From Newton’s Law of Universal
Gravitation
If this is the centripetal force keeping
the planet in orbit then
G Mm = mv2 (from centripetal equation)
r2
r
 GM = v2
r
If T is the time for the planet to make one
orbit
v = 2 r v2 = 222 r2
T
T2
 GM = 4 2 r 2 r
T2
 GM = 4 2 r 3
T2
 r 3 = GM
T2
4 2
 r3=
a constant
T2
Kepler´s Third Law
The square of the times of revolution of
the planets (i.e. Their periodic time T )
about the sun are proportional to the
cubes of their mean distance (r) from it.
We have considered a circular orbit but
more advanced mathematics gives the
same result for an elliptical one.
Energy of Orbiting Satellites
Potential Energy, Ep
A satellite of mass m orbiting the Earth at a
distance r from its centre has
Gravitational Potential, V = - G Me
r
Therefore the gravitational potential energy,
Ep = - G Mem
r
Energy of Orbiting Satellite
Kinetic Energy, Ek
By the law of Universal Gravitation and
Newton’s Second Law
G Mem = mv2
r2
r
Therefore the kinetic energy,
Ek = ½mv2 = G Mem
2r
Energy of Orbiting Satellite
Total Energy, Ep+ Ek
Total Energy = - G Mem + G Mem
r
2r
Total Energy = - G Mem
2r
Total energy is constant for a
circular orbit.
Graphs of Energy Against
Radius
Potential Energy
Ep
Ep
r
1/r
i.e. Ep  -1/r
or Ep = -k/r
where k is the constant of proportionality
= GMem
Graphs of Energy Against
Radius
Kinetic Energy
Ek
Ek
r
1/r
i.e. Ek  1/r
or Ek = k/r
where k is the constant of proportionality
= GMem
2
Graphs of Energy Against
Radius
Total Energy
Etotal
Etotal
r
1/r
i.e. Etotal  -1/r
or Etotal = -k/r
where k is the constant of proportionality
= GMem
2
Weightlessness
Consider an object of mass m hanging
from a spring balance which is itself
hanging from the roof of a lift
T
mg
a
The body is subjected to a downward
directed force mg due to the Earth, and an
upwards force T, due to the tension in the
spring.
The net down ward force is (mg – T ), and by
Newton´s second law
mg – T = ma
Where a is downward directed acceleration of
the body
If the lift is stationary, or is moving with a
constant speed, a = 0 and therefore T = mg
i.e. The balance registers the weight of the
body as mg
However, if the lift is falling freely under
gravity, both it and the body have a
downward directed acceleration of g
i.e. g = a
It follows from the equation that T = 0
i.e. The balance registers the weight of the
body as zero
It is usual to refer to a body in this situation
as being weightless
The term should be used with care, a
gravitational pull of magnitude mg acts on
the body whether it is in free fall or not, and
therefore, in the strictest sense it has weight
even when in free fall.
The reason it is said to be weightless is that,
whilst falling freely, it exerts no force on its
support.
Similarly, a man standing on the floor of a lift
would exert no force on the floor if the lift
were in free fall. In accordance with
Newton´s third law, the floor of the lift would
exert no upwards push on the man and
therefore he would not have the sensation of
weight.
Orbital Weightlessness
An astronaut in an orbiting spacecraft has a
centripetal acceleration equal to g1, where g1
is the acceleration due to gravity at the
height of the orbit
The spacecraft also has the same centripetal
acceleration
The astronaut therefore has no acceleration
relative to his spacecraft, i.e. he is weightless