Download Stat 281 Chapter 9

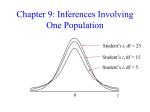
Chapter 9: Inferences Involving
One Population
Student’s t, df = 25
Student’s t, df = 15
Student’s t, df = 5
0
t
Estimation of m (s unknown)
• We have seen how to form confidence intervals for m when
we have a normal distribution and known s, using the z
distribution.
• We now turn to the situation where s is unknown but the
sample size is large or the sample population is normal.
• Since s is unknown, we use s in its place.
• However, without knowing s, we are not able to make use
of the z table in building a confidence interval.
• Instead, we will use a distribution called t (Student’s t).
• The t distribution is symmetric and bell-shaped like the
standard normal, and also has a m=0, but s>1, so the shape
is flatter in the middle and thicker in the tails.
Student’s t-Distributions:
Normal distribution
Student’s t, df = 15
Student’s t, df = 5
0
t
Degrees of Freedom, df:
A parameter that identifies each different distribution of
Student’s t-distribution. For the methods presented in this
chapter, the value of df will be the sample size minus 1, df = n
- 1.
Using t
• As the previous graph shows, the t distribution has
another parameter, called degrees of freedom (df).
So this is actually a family of distributions, with
different df values.
• The higher the df, the closer the t distribution
comes to the standard normal.
• For our purposes, df=n-1. It is actually related to
the denominator in the formula for s2.
• There is a t-table in the back of the book. It is
different from the z-table, so we have to
understand how it works.
The t table
• Refer to the table. First you will notice the lefthand column is for df.
• When df ≥100, the z-table can be used, because the
values will be very close.
• This table gives tail probabilities, similar to z(a).
However, only a selection of probabilities is given,
across the top in red.
• The interior of the table gives the t-values, so it is
arranged almost opposite of the z-table.
• The notation used for t-values is t(df,a).
• Just like z(a), a refers to the upper tail probability.
t-Distribution Showing t(df, a):
a
0
t (df ,a )
t
Confidence Intervals
• When we build our confidence interval, a
refers to the probability in both tails.
• This is not the same a used in looking up
the distribution! So what we have to look
up is actually a/2, because that’s the upper
tail probability.
• And so we come to the formula for a
(1-a)100% CI for m when s is unknown:
x  t( df ,a / 2) sx
Example: Find the value of t(12, 0.025).
0.025
0.025
- t (12,0.025)
- 2.18
Portion of
Table 6
df

12
0
t (12,0.025)
2.18
t
Amount of a in one-tail


0.025
2.18
Example: A study is conducted to learn how long it takes the
typical tax payer to complete his or her federal income tax
return. A random sample of 17 income tax filers showed a
mean time (in hours) of 7.8 and a standard deviation of 2.3.
Find a 95% confidence interval for the true mean time
required to complete a federal income tax return. Assume the
time to complete the return is normally distributed.
Solution:
1. Parameter of Interest: the mean time required to complete
a federal income tax return.
2. Confidence Interval Criteria:
a. Assumptions: Sampled population assumed normal, s
unknown.
b. Distribution table value: t will be used.
c. Confidence level: 1 - a = 0.95
3. The Sample Evidence:
n = 17, x = 7.8, and
s = 2.3
4. Calculations:
t (df ,a / 2) = t (16,0.025) = 2.12
s
2.3
=
= 0.5578
n
17
x  t( df ,a / 2) sx = 7.8  (2.12)(.5578)
(7.8 - 1.18, 7.8  1.18)
= (6.62, 8.98)
5. (6.62, 8.98) is the 95% confidence interval for m.
Hypothesis test involving m,
s unknown
• We have seen how to conduct hypothesis tests involving m
when we have a normal distribution and known s, using
the z distribution.
• We now turn to the situation where s is unknown but x has
a normal distribution (because the sample size is large or
the sample population is normal).
• Since s is unknown, we use s in its place.
x-m
• However, the random variable s / n does not have a have
a standard normal distribution so we do not call it z* and
we cannot refer to the z table for comparison.
• Instead, the we will use the t distribution, and the test
statistic will be
x-m
t* =
with df = n - 1
s n
Example: A random sample of 25 students
registering for classes showed the mean waiting time
in the registration line was 22.6 minutes and the
standard deviation was 8.0 minutes. Is there any
evidence to support the student newspaper’s claim
that registration time takes longer than 20 minutes?
Use a = 0.05 and assume waiting time is
approximately normal.
Solution:
1. State the null and alternative hypotheses :
H0: m = 20 () (no longer than)
Ha: m > 20 (longer than)
2.
3.
4.
Determine the distribution to use:
The sampled population is approximately normal.
s is unknown.
Use t with df = n - 1 = 24
Determine the Rejection Region or Decision Rule:
This is a right-tailed test with a=.05, so we
reject H0 if t*  t(24,.05) = 1.71 .
Calculate the test statistic:
t* =
5.
x - m 22.6 - 20 2.6
=
=
= 1.625
s n
8 25
1.6
State the conclusion: We do not reject H0, so we do not
have sufficient evidence to support the student
newspaper’s claim that registration time takes longer
than 20 minutes, in other words, we will assume the true
registration time is less than or equal to 20 minutes.
Using the p-value procedure:
p = P(t > t*) = P(t > 1.625)
Note:
1. If this hypothesis test is done with the aid of a computer a
fairly precise p-value can be calculated. Using the table,
we are somewhat limited by the probabilities available.
2. Using Table 6: place bounds on the p-value.
0.05 < p < 0.10
3. Using Table 7: read the p-value directly from the table for
many situations.
p  0.061
The p-value is not smaller than the level of significance, a.
Binomial Parameter p
1. p is the binomial parameter, the probability of success on
a single trial.
2. p’ is the observed or sample binomial probability.
x
x represents the number of successes that
p' =
n occur in a sample consisting of n trials.
3. For the binomial random variable x:
m = np,
s = npq ,
where
q = 1- p
4. The distribution of x is approximately normal if n is larger
than 20 and if np and nq are both larger than 5.
Sampling Distribution of p’:
If a sample of size n is randomly selected from a large
population with p = P(success), then the sampling distribution
of p’ has
1. a mean m p ' equal to p,
2. a standard error s p ' equal to ( pq) / n , and
3. an approximately normal distribution if n is sufficiently
large.
In practice, use of the following guidelines will ensure
normality:
1. The sample size is greater than 20.
2. The sample consists of less than 10% of the population.
3. The products np and nq are both larger than 5.
The assumptions for inferences about the binomial
parameter p:
The n random observations forming the sample are selected
independently from a population that is not changing during
the sampling.
Confidence Interval Procedure:
The unbiased sample statistic p’ is used to estimate the
population proportion p.
A (1-a)100% confidence interval for p is given by
p ' za / 2
p'q'
n
where p' = x / n and q' = 1 - p'
Example: A recent survey of 300 randomly selected fourth
graders showed 210 participate in at least one organized sport
during one calendar year. Find a 95% confidence interval for
the proportion of fourth graders who participate in an
organized sport during the year.
Solution:
1. Describe the population parameter of concern:
The parameter of interest is the proportion of fourth
graders who participate in an organized sport during the
year.
2. Specify the confidence interval criteria:
a. Check the assumptions.
The sample was randomly selected.
Each subject’s response was independent.
b. Identify the probability distribution:
z is the test statistic.
p’ is approximately normal
n = 300 > 20
np ' = 300(210 / 300) = 210 > 5
nq ' = 300(90 / 300) = 90 > 5
c. Determine the level of confidence: 1 - a = 0.95
3. Collect and present sample evidence.
Sample information: n = 300, and x = 210.
The point estimate: p' = x / n = 210 / 300 = 0.70
4. Determine the confidence interval:
a. Determine the confidence coefficients:
Using Table 4, Appendix B: z (a / 2) = z (0.025) = 1.96
b. The error bound:
p' q'
(0.70)(0.30)
E = z (a / 2) 
= 1.96
n
300
= (1.96) 0.0007 = (1.96)(0.0265) = 0.0519
c. Find the lower and upper confidence limits:
p ' E
(0.70 - 0.0519, 0.70  0.0519)
(0.6481, 0.7519)
d. The Results:
(0.6481, 0.7519) is a 95% confidence interval for the
true proportion of fourth graders who participate in an
organized sport during the year.
Sample Size Determination:
[ z (a / 2)]2  p * q *
n=
E2
E: maximum error of estimate.
1 - a: confidence level
p*: provisional value of p (q* = 1 - p*)
If no provisional values for p and q are given use p* = q* = 0.5
(Always round up.)
Example: Determine the sample size necessary to estimate the
true proportion of laboratory mice with a certain genetic defect.
We would like the estimate to be within 0.015 with 95%
confidence.
Solution:
1. Level of confidence: 1 - a = 0.95, z(a/2) = z(0.025) = 1.96
2. Desired maximum error is E = 0.015.
3. No estimate of p given, use p* = q* = 0.5
4. Use the formula for n:
[ z (a / 2)]2  p * q * (1.96) 2  (0.5)  (0.5)
n=
=
2
E
(0.015) 2
0.9604
=
= 4268.44  n  4269
0.000225
Note: Suppose we know the genetic defect occurs in
approximately 1 of 80 animals.
Use p* = 1/80 = 0.125
[ z (a / 2)]2  p * q * (1.96) 2  (0.0125)  (0.9875)
n=
=
2
E
(0.015) 2
0.0474
=
= 210.75  n  211
0.000225
As illustrated here, it is an advantage to have some indication
of the value expected for p, especially as p becomes
increasingly further from 0.5.
Hypothesis-Testing Procedure:
For hypothesis tests concerning the binomial parameter p, use
the test statistic z*:
p '- p0
z* =
p0 q0
n
where
x
p' =
n
Example (Probability-Value Approach): A hospital
administrator believes that at least 75% of all adults have a
routine physical once every two years. A random sample of
250 adults showed 172 had physicals within the last two
years. Is there any evidence to refute the administrator's
claim? Use a = 0.05.
Solution:
1. State the null and alternative hypotheses:
H0: p = 0.75
Ha: p < 0.75
2. Determine the Distribution:
a. Assumptions: 250 adults independently surveyed, a
binomial distribution.
b. Test statistic: z*.
n = 250
np = (250)(0.75) = 187.5 > 5
nq = (250)(0.25) = 62.5 > 5
c. Level of significance: a = 0.05
3. Decision Rule: Reject H0 if p<.05.
4. Calculating the test statistic:
a. Sample information:
n = 250, x = 172, and p' = 172 / 250 = 0.688
b. The test statistic:
p '- p0
0.688 - 0.75
z* =
=
p0 q0
(0.75)(0.25)
250
n
-0.062
-0.062
=
=
= -2.26
0.00075 0.02738
p-value
- 2.26
0
z
p = P( z  -2.26) = 0.5000 - 0.4881 = 0.0119
b. The p-value is smaller than the level of significance, a.
5. Conclusion: There is evidence to suggest the proportion of
adults who have a routine physical exam every two years is
less than 0.75.
Example (Classical Procedure): A university bookstore
employee in charge of ordering texts believes 65% of
all students sell their statistics book back to the
bookstore at the end of the class. To test this claim,
200 statistics students are selected at random and 141
plan to sell their texts back to the bookstore. Is there
any evidence to suggest the proportion is different from
0.65? Use a = 0.01.
Solution:
1. The null and alternative hypotheses:
H0: p = 0.65
Ha: p  0.65
2. Determine the Distribution:
a. Assumptions: Sample randomly selected. Each
subject’s response was independent of other responses.
b. Test statistic: z*
n = 200
np = (200)(0.65) = 130 > 5 ; nq = (200)(0.35) = 70 > 5
c. Level of significance: a = 0.01
3. Decision Rule: Reject H0 if z*>2.58 or z*<-2.85
4. Calculate the value of the test statistic:
p '- p0
0.705 - 0.65
z* =
=
p0 q0
(0.65)(0.35)
200
n
0.055
0.055
=
=
= 1.63
0.0011375 0.03373
5.
Conclusion: There is no evidence to suggest the true
proportion of students who sell their statistics text back
to the bookstore is different from 0.65.
Note:
1. There is a relationship between confidence intervals and
two-tailed hypothesis tests when the level of confidence
and the level of significance add up to 1.
2. The confidence interval and the width of the noncritical
region are the same.
3. The point estimate is the center of the confidence interval,
and the hypothesized mean is the center of the noncritical
region.
4. If the hypothesized value of p is contained in the
confidence interval, then the test statistic will be in the
noncritical region.
5. If the hypothesized value of p does not fall within the
confidence interval, then the test statistic will be in the
critical region.