Download 3.2 Use Parallel Lines and Transversals

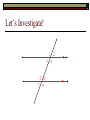
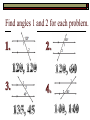
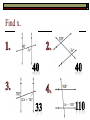
BELL RINGER






Lines q, r, and s are distinct in a plane. If line q is
perpendicular to line r, and line r is perpendicular to
s, then which of following is true?
q parallel s
q perpendicular to s
Q and s are skew
Q intersects s
S is a transversal of q and r
BELL RINGER cont.









Draw a line and label it line q.
Draw a line that is perpendicular to line q and label
this line r.
Draw a line s that is perpendicular to r.
What do you see? Remember choices…
q parallel s
q perpendicular to s
Q and s are skew
Q intersects s
S is a transversal of q and r
Chapter 3
Parallel and Perpendicular Lines
Lesson 3.2: Use Parallel Lines and Transversals
LEARNING TARGET
Solve problems using the corresponding angles postulate, alternate interior angles
theorem, alternate exterior angles theorem and consecutive interior angles theorem.
Let’s Investigate!
1
3 4
5 6
7 8
2
Postulate 15

Corresponding Angles
If two parallel lines
are cut by a transversal
then the pairs of
corresponding angles
are congruent.

2  6 3  7
1  5 4  8
1
3 4
5 6
7 8
2
Theorem 3.1

Alternate Interior Angles Theorem
If two parallel lines are cut by a
transversal, then the
1 2
3 4
pairs of alternate
interior angles are
5 6
congruent.

4  5
3  6
7 8
Theorem 3.2

Alternate Exterior Angles Theorem
If two parallel lines are cut by a transversal,
then the pairs of alternate exterior angles
1 2
are congruent.

3 4
1  8
2  7
5 6
7 8
Theorem 3.3

Consecutive Interior Angles Theorem
If two parallel lines are cut by a transversal, then
the pairs of consecutive interior angles
are supplementary.

1
3 4
3  5  180
4  6  180
5 6
7 8
2
Find angles 1 and 2 for each problem.
Let’s Try!

Find the value of x.
m4  ( x  5)  180
115  ( x  5)  180
x  60
115o
4
(x + 5)o
Find x.
Example 1 – Use properties of parallel lines
Find the value of x.
Example 2 – Use properties of parallel lines
Find the value of x.
Example 3 – Use properties of parallel lines
Find the value of x and y.
Example 4 – Use properties of parallel lines
Find the value of x and y.
Homework

Page 157

4-18 even, 22,28