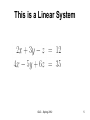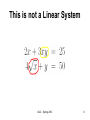Download Lecture6

GUC - Spring 2012
1
Lecture 6
Linear Algebra (III)
Linear Systems of
Equations
GUC - Spring 2012
2
Linear System of Equations
• A system of m-linear equations in n
variables x1, x2, ..., xn has the general form
(1)
GUC - Spring 2012
3
Linear System of Equations
• where the coefficients aij(i = 1, 2, ...,m;
j = 1, 2, ..., n)
• and the quantities bi
• are all known scalars (numbers).
GUC - Spring 2012
4
This is a Linear System
GUC - Spring 2012
5
This is not a Linear System
GUC - Spring 2012
6
Matrix Representation of a
Linear System of Equations
• Any linear system of the form (1) can be
written in the matrix form
AX = B
GUC - Spring 2012
7
Matrix Representation of a
Linear System of Equations
• With
A is the coefficient matrix
GUC - Spring 2012
8
Matrix Representation of a
Linear System of Equations
X is the column of variables
GUC - Spring 2012
9
Matrix Representation of a
Linear System of Equations
B is the column of constants
GUC - Spring 2012
10
Example
• Can be represented as
 x
2 3  1   12 
4  5 6   y   35

 z   
 
GUC - Spring 2012
11
Example
• The matrix form
• Represents the system
GUC - Spring 2012
12
Gauss Elimination Method
• The method consists of four steps
 1. Construct an augmented matrix for the
given system of equations.
 2. Use elementary row operations to
transform the augmented matrix into an
augmented matrix in row-reduced form.
 3. Write the equations associated with the
resulting augmented matrix.
 4. Solve the new set of equations by back
substitution.
GUC - Spring 2012
13
Augmented Matrix
• The augmented matrix for AX = B is the
partitioned matrix [A|B]
• E.g.
• has its augmented matrix as
GUC - Spring 2012
14
Elementary Row Operations
elementary row operations are :
• 1- Interchange any two rows in a matrix
• 2- Multiply any row of a matrix by a
nonzero scalar
• 3- Add to one row of a matrix a scalar
times another row of the same matrix
GUC - Spring 2012
15
Row-Reduced Form
•
A matrix is in row-reduced form if it satisfies the
following four conditions:
1.
All zero rows appear below nonzero rows when both
types are present in the matrix.
2. The first nonzero element in any nonzero row is 1.
3. All elements directly below (that is, in the same column
but in succeeding rows form) the first (left- to- right)
nonzero element of a nonzero row are 0 .
4. The first nonzero element of any nonzero row appears
in a later column (further to right) than the first nonzero
element in any preceding row.
GUC - Spring 2012
16
Example
• Use Gaussian elimination to solve the
system
GUC - Spring 2012
17
Step 1
The augmented matrix
• The augmented matrix of the system is:
GUC - Spring 2012
18
Step 2
Elementary row operations
We use elementary row operations to
transform the augmented matrix into
row-reduced form as follows,
GUC - Spring 2012
19
GUC - Spring 2012
20
GUC - Spring 2012
21
GUC - Spring 2012
22
GUC - Spring 2012
23
GUC - Spring 2012
24
This is a Row Reduced Form
GUC - Spring 2012
25
Step 3
The Resulting System
• We write the equations
augmented matrix
GUC - Spring 2012
of
the
resulting
26
Step 3
Writing the Resulting System
• We write the equations associated with the
resulting augmented matrix
GUC - Spring 2012
27
Step 4
Solving the Resulting System
• we Solve the derived set of equations by back
substitution.
• The third equation implies that z = 5,
• Substituting in the second equation, we get y =
12 − 15 = −3,
• substituting with the values of z and y in the first
equation, we get x = 4
GUC - Spring 2012
28
Example
• Use Gauss elimination method to solve
the linear system of equations
GUC - Spring 2012
29
Example
1 0 
I2  

0
1


1 0 0 
I 3  0 1 0


0 0 1
GUC - Spring 2012
30
The Augmented Matrix
GUC - Spring 2012
31
Getting Row Reduced Form
GUC - Spring 2012
32
Getting Row Reduced Form
GUC - Spring 2012
33
Writing the Resulting System
• The resulting system of equations is
GUC - Spring 2012
34
Solving the Equations
• Solving the last system by
substitution, we get the solution
back
• x = 1 and y = 1
GUC - Spring 2012
35
Example
• Use Gauss elimination method to solve
the linear system of equations
GUC - Spring 2012
36
The Augmented Matrix
GUC - Spring 2012
37
Getting Row Reduced Form
GUC - Spring 2012
38
Getting Row Reduced Form
GUC - Spring 2012
39
Writing the Resulting System
GUC - Spring 2012
40
Important Note
• Since the final system has the number of
variables (4) greater than the number of
equations (3),
• then one of the variable will be arbitrary,
• and the other variables will be found in
terms of it.
GUC - Spring 2012
41
Solving The Resulting System
• The solution will be found in terms of x4 as
follows,
GUC - Spring 2012
42
Note
• Since x4 is arbitrary, then the system has
infinite number of solutions, depending on
the value of x4
• for example if you choose
• Then,
GUC - Spring 2012
43
Japan !
GUC - Spring 2012
44
No Comment
GUC - Spring 2012
45