* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 15
Valve RF amplifier wikipedia , lookup
Broadcast television systems wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Electronic paper wikipedia , lookup
Opto-isolator wikipedia , lookup
Standing wave ratio wikipedia , lookup
Current mirror wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Power electronics wikipedia , lookup
Electrical ballast wikipedia , lookup
Index of electronics articles wikipedia , lookup
Surge protector wikipedia , lookup
Rectiverter wikipedia , lookup
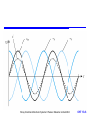
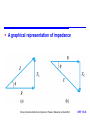
Alternating Voltages and Currents Chapter 15 Introduction Voltage and Current Reactance of Inductors and Capacitors Phasor Diagrams Impedance Complex Notation Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Introduction 15.1 From our earlier discussions we know that v Vp sin ( t ) where Vp is the peak voltage is the angular frequency is the phase angle Since = 2f it follows that the period T is given by T 1 2 f Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› If is in radians, then a time delay t is given by / as shown below Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Voltage and Current 15.2 Consider the voltages across a resistor, an inductor and a capacitor, with a current of i IP sin(t ) Resistors – from Ohm’s law we know v R iR – therefore if i = Ipsin(t) v R IP R sin(t ) Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Voltage and Current Inductors - in an inductor 15.2 di vL L dt – therefore if i = Ipsin(t) d(IP sin(t )) LIP cos(t ) dt 1 Capacitors - in a capacitor vC idt C – therefore if i = Ipsin(t) vL L Ip 1 vC IP sin(t ) cos(t ) C C Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Reactance of Inductors and Capacitors 15.3 Let us ignore, for the moment the phase angle and consider the magnitudes of the voltages and currents Let us compare the peak voltage and peak current Resistance Peak value of voltage Peak value of (IP Rsin(t )) IP R R Peak value of current Peak value of (IP sin(t )) IP Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Inductance Peak value of voltage Peak value of (LIP cos(t )) LIP L Peak value of current Peak value of (IP sin(t )) IP Capacitance Peak value of voltage Peak value of current Peak value of ( Ip C cos(t )) Peak value of (I p sin(t )) Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 Ip 1 C Ip C OHT 15.‹#› The ratio of voltage to current is a measure of how the component opposes the flow of electricity In a resistor this is termed its resistance In inductors and capacitors it is termed its reactance Reactance is given the symbol X Therefore Re ac tan ce of an inductor, X L L Reactance 1 Reactance Re ac tan ce of a capacitor, XC C Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Since reactance represents the ratio of voltage to current it has units of ohms The reactance of a component can be used in much the same way as resistance: – for an inductor V I XL – for a capacitor V I XC Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Example – see Example 15.3 from course text A sinusoidal voltage of 5 V peak and 100 Hz is applied across an inductor of 25 mH. What will be the peak current? At this frequency, the reactance of the inductor is given by X L L 2fL 2 100 25 10 3 15.7 Therefore VL 5 IL 318 mA peak X L 15.7 Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Phasor Diagrams 15.4 Sinusoidal signals are characterised by their magnitude, their frequency and their phase In many circuits the frequency is fixed (perhaps at the frequency of the AC supply) and we are interested in only magnitude and phase In such cases we often use phasor diagrams which represent magnitude and phase within a single diagram Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Examples of phasor diagrams (a) here L represents the magnitude and the phase of a sinusoidal signal (b) shows the voltages across a resistor, an inductor and a capacitor for the same sinusoidal current Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Phasor diagrams can be used to represent the addition of signals. This gives both the magnitude and phase of the resultant signal Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Phasor diagrams can also be used to show the subtraction of signals Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Phasor analysis of an RL circuit See Example 15.5 in the text for a numerical example Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Phasor analysis of an RC circuit See Example 15.6 in the text for a numerical example Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Phasor analysis of an RLC circuit Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Phasor analysis of parallel circuits in such circuits the voltage across each of the components is the same and it is the currents that are of interest Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Impedance 15.5 In circuits containing only resistive elements the current is related to the applied voltage by the resistance of the arrangement In circuits containing reactive, as well as resistive elements, the current is related to the applied voltage by the impedance, Z of the arrangement – this reflects not only the magnitude of the current but also its phase – impedance can be used in reactive circuits in a similar manner to the way resistance is used in resistive circuits Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Consider the following circuit and its phasor diagram Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› From the phasor diagram it is clear that that the magnitude of the voltage across the arrangement V is V VR 2 VL 2 (IR )2 (IX L )2 I R 2 XL2 IZ where Z R 2 X L 2 Z is the magnitude of the impedance, so Z =|Z| Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› From the phasor diagram the phase angle of the impedance is given by tan 1 VL IX X tan -1 L tan -1 L VR IR R This circuit contains an inductor but a similar analysis can be done for circuits containing capacitors In general Z R X 2 2 and tan 1 Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 X R OHT 15.‹#› A graphical representation of impedance Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Complex Notation 15.6 Phasor diagrams are similar to Argand Diagrams used in complex mathematics We can also represent impedance using complex notation where Resistors: ZR = R Inductors: ZL = jXL = Capacitors: ZC = -jXC = jL 1 1 j C jC Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Graphical representation of complex impedance Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Series and parallel combinations of impedances – impedances combine in the same way as resistors Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Manipulating complex impedances – complex impedances can be added, subtracted, multiplied and divided in the same way as other complex quantities – they can also be expressed in a range of forms such as the rectangular, polar and exponential forms – if you are unfamiliar with the manipulation of complex quantities (or would like a little revision on this topic) see Appendix D of the course text which gives a tutorial on this subject Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Example – see Example 15.7 in the course text Determine the complex impedance of this circuit at a frequency of 50 Hz. At 50Hz, the angular frequency = 2f = 2 50 = 314 rad/s Therefore Z Z C Z R Z L R j( X L XC ) R j(L 200 j(314 400 10 3 1 314 50 10 6 1 ) C ) 200 j62 ohms Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Using complex impedance Example – see Section 15.6.4 in course text Determine the current in this circuit. Since v = 100 sin 250t , then = 250 Therefore Z R j XC Rj 1 C 100 j 1 250 10 4 100 j40 Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Example (continued) The current is given by v/Z and this is easier to compute in polar form Z 100 j40 Z 1002 402 107.7 Z tan 1 40 21.8 100 Z 107.7 21.8 Therefore i v 1000 0.9321.8 Z 107.7 21.8 Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› A further example A more complex task is to find the output voltage of this circuit. The analysis of this circuit, and a numerical example based on it, are given in Section 15.6.4 and Example 15.8 of the course text Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#› Key Points A sinusoidal voltage waveform can be described by the equation v Vp sin ( t ) The voltage across a resistor is in phase with the current, the voltage across an inductor leads the current by 90, and the voltage across a capacitor lags the current by 90 The reactance of an inductor XL = L The reactance of a capacitor XC = 1/C The relationship between current and voltage in circuits containing reactance can be described by its impedance The use of impedance is simplified by the use of complex notation Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 15.‹#›