Download Slide 1 - msmatthewsschs

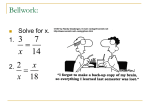
6.1 – Ratios, Proportions, and the Geometric Mean
Ratio: The relationship between 2 numbers,
has no units
a:b
a
b
Always simplify them!!!
a to b
Find the ratio of the width to the length of the
rectangle. Then simplify the ratio.
4 cm
1

12 cm 3
Find the ratio of the width to the length of the
rectangle. Then simplify the ratio.
6in
3

10in
5
Find the ratio of the width to the length of the
rectangle. Then simplify the ratio.
12in 2

18in 3
Use the number line to find the ratio of the
distances.
AB
AC
2
1

6
3
Use the number line to find the ratio of the
distances.
AB
CD
2
3
Use the number line to find the ratio of the
distances.
AE
BC
14 7

4
2
Use the number line to find the ratio of the
distances.
AE
AB
14 7

2
1
Proportion:
An equation that states two ratios are
equal
a c
b
To solve:

d
Cross multiply!
ad = bc
Solve the proportion.
3 x

4 12
4x = 36
4
4
x=9
3 x

4
12
1
3
x=9

Solve the proportion.
1 3

3 y
y = 9
1 3

3 y
y=9
Solve the proportion.
2
4

x  2 10
1
1
2
2
4

x  2 10
5
4(x + 2) = 20
4x + 8 = 20
4x = 12
x=3
x+2=5
x=3
Solve the proportion.
3
6

x x8
3(x + 8) = 6x
3x + 24 = 6x
24 = 3x
8=x
1
2
3
6

x x8
2x = x + 8
x=8
Solve the proportion.
x x  12

24
8
x x  12

24
8
3
24(x – 12) = 8x
24x – 288 = 8x
–288 = –16x
18 = x
1
3x – 36 = x
2x – 36 = 0
2x = 36
x = 18
Solve the proportion.
2
4

y 1 y  4
4(y + 1) = 2(y + 4)
4y + 4 = 2y + 8
2y + 4 = 8
2y = 4
y=2
1
2
2
4

y 1 y  4
2y + 2 = y + 4
y+2=4
y=2
The ratio of two side lengths for the triangle is
given. Solve for the variable.
AC:AB is 2:3.
2
x

3 12
3x = 24
3
3
x=8
2 x

3 12
1
4
x=8
The ratio of two side lengths for the triangle is
given. Solve for the variable.
1
1
8
2 16 x
AB:CB is 2:1.
2 16 x

1

24
16x = 48
16
16
x=3
1
24
3
x=3
The ratio of two side lengths for the triangle is
given. Solve for the variable.
1
3
7
AC:BC is 7:4.
21 7  21
4

2x  4 4
7(2x + 4) = 84
14x + 28 = 84
14x = 56
x=4
2x  4
2x + 4 = 12
2x = 8
x=4
Sally received a 64% on a 150 point test. How
many points did she earn on the test?
32
64
x

100 150
64
x

100 150
1
100x = 9600
100
100
x = 96
2
3
x = 96
If Taylor has a batting average of 0.275 and has
had 640 at bats, how many hits has he made?
x
0.275

640
1
x = 176
Geometric Mean:
The square root of the product of two numbers
a x

x b
x2 = ab
x  ab
Find the geometric mean.
1 and 4
x  ab
x  1 4
x 4
x2
Find the geometric mean.
2 and 50
x  ab
x  2  50
x  100
x  10
Find the geometric mean.
3 and 15
x  ab
x  3 15
x  45
x3 5
Find the geometric mean.
7 and 14
x  ab
x  7 14
x  98
x7 2
HW Problem
6.1
360-362
11-19 odd, 23-35 odd, 39-43 odd,
49, 51, 79, 80
# 19
2
x

9 36
Ans: AB = 8
BC = 28