* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Python Programming: An Introduction to Computer - comp
Pattern recognition wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Inverse problem wikipedia , lookup
Computational phylogenetics wikipedia , lookup
Theoretical computer science wikipedia , lookup
Determination of the day of the week wikipedia , lookup
Algorithm characterizations wikipedia , lookup
History of the Church–Turing thesis wikipedia , lookup
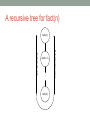
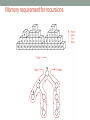
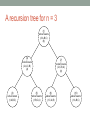
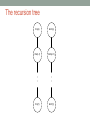
7. RECURSIONS Rocky K. C. Chang October 12, 2015 Objectives • To be able to design recursive solutions to solve "simple" problems. • To understand the relationship between recursion and mathematical induction. • To understand that recursion is a postponement of work. • To know how to design recursive algorithms systematically. WHAT IS RECURSION? Example 1: Computation of n! • Standard method: • fact(n) = 1 * 2 * … * n • Recursive method: • fact(n) = n * fact(n-1) • fact(n-1) = (n-1) * fact(n-2) • … • fact(2) = 2 * fact(1) • fact(1) = 1 * fact(0) • fact(0) = 1 EXERCISE 7.1 Implement a recursive function to compute n!. Example 2: Birthday cake cutting • Question: how many pieces of a circular cake as a result of n cuts through the center? • Write down your answer here. Example 2 • Recursive approach: Example 3: Fibonacci numbers • The rabbit population problem: • Start out with a male-female pair of rabbits. • It takes two months for each pair to be reproductive. • Each pair reproduces another male-female pair in each subsequent month. • How many pairs of male-female rabbits after n months if no rabbits die during this period? • Standard method: • 1st month: 1 • 2nd month: 1 • 3rd month: 2 • 4th month: 3 • … Example 3 • Recursive method: • Just prior to the start of nth month, there are fib(n-1) pairs. • However, only fib(n-2) pairs can reproduce new pairs. • Therefore, fib(n) = ? RECURSION AND MATHEMATICAL INDUCTION Parallel w. mathematical induction • Mathematical induction is a very powerful theorem- proving technique. • Proving that a statement T(n) is true for n ≥ 1 requires the proofs for • (Base) T(1) is true. • (Induction) For every n > 1, if T(n-1) is true, then T(n) is true. Mathematical induction, e.g., • Prove that for all natural numbers x and n, xn – 1 is divisible by x – 1. • Base: when n = 1, xn – 1 is divisible by x – 1. • Induction: For n > 1, assume that xn-1 – 1 is divisible by x – 1. • Write xn - 1 = x(xn-1 – 1) + (x – 1). • Therefore, xn – 1 is also divisible by x – 1. Mathematical induction, e.g., • Prove that if n is a natural number and 1 + x > 0, then (1 + x)n ≥ 1 + nx. • Base: for n = 1, LHS = RHS = 1 + x. • Induction: For n ≥ 1, assume that (1 + x)n ≥ 1 + nx. • (1 + x)n+1 = (1 + x)(1 + x)n • (1 + x)n+1 ≥ (1 + x)(1 + nx) = 1 + (n + 1)x + nx2 • (1 + x)n+1 ≥ 1 + (n + 1)x The parallels • A recursive process consists of two parts: • A smallest case that is processed without recursion (base case) • A general method that reduces a particular case into one or more of the smaller cases (induction step) • Factorials • Base: • Induction: • The birthday cake cutting problem • Base: • Induction: • Fibonacci numbers • Base: • Induction: RECURSION AS A POSTPONEMENT OF WORK Tracing the recursive calls fact(6) = = = = = = = = = = = = = 6 * fact(5) 6 * (5 * fact(4)) 6 * (5 * (4 * fact(3))) 6 * (5 * (4 * (3 * fact(2)))) 6 * (5 * (4 * (3 * (2 * fact(1))))) 6 * (5 * (4 * (3 * (2 * (1 * fact(0)))))) 6 * (5 * (4 * (3 * (2 * (1 * 1))))) 6 * (5 * (4 * (3 * (2 * 1)))) 6 * (5 * (4 * (3 * 2))) 6 * (5 * (4 * 6)) 6 * (5 * 24) 6 * 120 720 A recursive tree for fact(n) fact(n) : : fact(0) Returning the values Invoking the calls fact(n-1) How does recursion work? • When a program is run, each execution of a method is called an activation. • The data objects associated with each activation are stored in the memory as an activation record. • Data objects include parameters, return values, return address and any variables that are local to the method. • A stack is a data structure to store all activation records in a correct order. A recursive tree for fib(n) Memory requirement for recursions HOW TO DESIGN RECURSIVE ALGORITHMS? Several important steps • Find the key step. • How can this problem be divided into parts? • Find a stopping rule. • It is usually the small, special case that is trivial or easy to handle without recursion. • Outline your algorithm. • Combine the stopping rule and the key step, using an if statement to select between them. • Check termination. • Verify that the recursion will always terminate. • Draw a recursion tree. MORE COMPLEX EXAMPLES Tower of Hanoi • Problem: To move a stack of n disks from pole A to pole B, subjecting to 2 rules: • Only one disk can be moved at a time. • A larger disk can never go on top of a smaller one. • n = 1, trivial • n = 2, trivial again • n = 3: trivial to some people? • n = 4: trivial to fewer people? • n = 64? Think recursively … Think recursively … A recursive solution • solveTowers(n, A, B, C) • n: the number of disks • moving the disks from A to B via C • no larger disks put on top of smaller disks • A recursive approach: • Base: trivial and solved for n = 1 • Induction; for n > 1, solveTowers(n, A, B, C) can be solved by • solveTowers(n - 1, A, C, B) // the top n-1 disks • solveTowers(1, A, B, C) // the largest disk • solveTowers(n - 1, C, B, A) // the top n-1 disks A recursion tree for n = 3 (1) solveTowers (3,A,B,C) (6) (2) solveTowers (2,A,C,B) (4) (3) solveTowers (1,A,B,C) (7) solveTowers (2,C,B,A) (9) (5) solveTowers (1,B,C,A) (8) solveTowers (1,C,A,B) (10) solveTowers (1,A,B,C) Computing • Write R(n) = Q(1) × Q(2) × Q(3) × … × Q(n), where • Q(1) = sqrt[½+ ½ sqrt(½)], • Q(2) = sqrt[½+ ½ Q(1)], …, • Q(n) = sqrt[½+ ½ Q(n – 1)], n > 1. • Therefore, • Base: R(1) = Q(1) • Induction: Given R(n – 1) and Q(n – 1), Q(n) = sqrt[½+ ½ Q(n – 1)] and R(n) = R(n – 1) × Q(n). The recursion tree rhs(n) term(n) rhs(n-1) term(n-1) : : : : rhs(1) term(1) Summary • Recursion is a divide-and-conquer approach to solving a complex problem. • Divide, conquer, and glue • Similar to mathematical induction, recursion has a “base” case and an “induction” step. • A recursion implementation essentially postpones the work until hitting the base case. • Recursions appear in many, many, …, different forms. Acknowledgments • The figures on pp. 19-20 are taken from • Robert L. Kruse and Alexander J. Ryba, Data Structures and Program Design in C++, Prentice-Hall, Inc., 1999. • The figures on pp. 25-26 are taken from • F. Carrano and J. Prichard, Data Abstraction and Problem Solving with JAVA Wall and Mirrors, First Edition, Addison Wesley, 2003. END