* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Turning Probabilistic Reasoning into Programming
Abstraction (computer science) wikipedia , lookup
Functional programming wikipedia , lookup
C Sharp (programming language) wikipedia , lookup
Go (programming language) wikipedia , lookup
Relational model wikipedia , lookup
Object-relational impedance mismatch wikipedia , lookup
Corecursion wikipedia , lookup
Turning Probabilistic
Reasoning into Programming
Avi Pfeffer
Harvard University
Uncertainty
Uncertainty is ubiquitous
Partial information
Noisy sensors
Non-deterministic actions
Exogenous events
Reasoning under uncertainty is a central
challenge for building intelligent systems
Probability
Probability provides a mathematically
sound basis for dealing with uncertainty
Combined with utilities, provides a basis
for decision-making under uncertainty
Probabilistic Reasoning
Representation: creating a
probabilistic model of the world
Inference: conditioning the model on
observations and computing
probabilities of interest
Learning: estimating the model from
training data
The Challenge
How do we build probabilistic models of
large, complex systems that are
easy to construct and understand
support efficient inference
can be learned from data
(The Programming Challenge)
How do we build programs for
interesting problems that are
easy to construct and maintain
do the right thing
run efficiently
Lots of Representations
Plethora of existing models
Bayesian networks, hidden Markov models,
stochastic context free grammars, etc.
Lots of new models
Object-oriented Bayesian networks,
probabilistic relational models, etc.
Goal
A probabilistic representation language
that
captures many existing models
allows many new models
provides programming-language like
solutions to building and maintaining
models
IBAL
A high-level “probabilistic programming”
language for representing
Probabilistic models
Decision problems
Bayesian learning
Implemented and publicly available
Outline
Motivation
The IBAL Language
Inference Goals
Probabilistic Inference Algorithm
Lessons Learned
Stochastic Experiments
A programming language expression describes
a process that generates a value
An IBAL expression describes a process that
stochastically generates a value
Meaning of expression is probability
distribution over generated value
Evaluating an expression = computing the
probability distribution
Simple expressions
Constants
Variables
Conditionals
x = ‘hello
y=x
z = if x==‘bye
ffthen 1 else 2
Stochastic Choice
w = dist [ 0.4: ’hello,
0.6: ’world ]
Functions
fair ( ) = dist [0.5 : ‘heads, 0.5 : ‘tails]
x = fair ( )
y = fair ( )
x and y are independent tosses of a
ftfair coin
Higher-order Functions
fair ( ) = dist [0.5 : ‘heads, 0.5 : ‘tails]
biased ( ) = dist [0.9 : ‘heads, 0.1 : ‘tails]
pick ( ) = dist [0.5 : fair, 0.5 : biased]
coin = pick ( )
x = coin ( )
y = coin ( )
x and y are conditionally independent
ffgiven coin
Data Structures and Types
IBAL provides a rich type system
tuples and records
algebraic data types
IBAL is strongly typed
automatic ML-style type inference
Bayesian Networks
Smart
Good Test
Taker
Exam
Grade
Diligent
Understands
HW
Grade
S
s
s
s
s
D P(U| S, D)
d 0.9 0.1
d 0.3 0.7
d 0.6 0.4
d 0.01 0.99
nodes = domain variables
edges = direct causal influence
Network structure encodes conditional independencies:
I(HW-Grade , Smart | Understands)
BNs in IBAL
D
S
smart = flip 0.8
G
U
diligent = flip 0.4
E
H
understands =
case <smart,diligent> of
# <true,true> : flip 0.9
# <true,false> : flip 0.6
…
First-Order HMMs
H1
H2
Ht-1
Ht
O1
O2
Ot-1
Ot
Initial distribution P(H1)
Transition model P(Hi|Hi-1)
Observation model P(Oi|Hi)
What if hidden state is arbitrary data
structure?
HMMs in IBAL
init : () -> state
trans : state -> state
obs : state -> obsrv
sequence(current) = {
state = current
observation = obs(state)
future = sequence(trans(state)) }
hmm() = sequence(init())
SCFGs
S -> AB (0.6)
S -> BA (0.4)
A -> a (0.7)
A -> AA (0.3)
B -> b (0.8)
B -> BB (0.2)
Non-terminals are data generating
functions
SCFGs in IBAL
append(x,y) =
if null(x) then y else
cons (first(x), append (rest(x),y)
production(x,y) = append(x(),y())
terminal(x) = cons(x,nil)
s() = dist[0.6:production(a,b),
0.4:production(b,a)]
a() = dist[0.7:terminal(‘a),…
Probabilistic Relational Models
Actor
Appearance
Actor
Movie
Gender
Actor
Chaplin
Role-Type
…
Chaplin Mod T.
…
…
Movie
Genre
Role-Type Actor.Gender, Movie.Genre
Movie
Mod T.
…
PRMs in IBAL
movie( ) = { genre = dist ... }
actor( ) = { gender = dist ... }
appearance(a,m) = {
role_type = case (a.gender,m.genre) of
(male,western) : dist ... }
mod_times = movie()
chaplin = actor()
a1 = appearance(chaplin, mod_times)
Other IBAL Features
Observations can be inserted into programs
condition probability distribution over values
Probabilities in programs can be learnable
parameters, with Bayesian priors
Utilities can be associated with different
outcomes
Decision variables can be specified
influence diagrams, MDPs
Outline
Motivation
The IBAL Language
Inference Goals
Probabilistic Inference Algorithm
Lessons Learned
Goals
Generalize many standard frameworks
for inference
e.g. Bayes nets, HMMs, probabilistic CFGs
Support parameter estimation
Support decision making
Take advantage of language structure
Avoid unnecessary computation
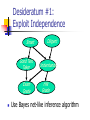
Desideratum #1:
Exploit Independence
Smart
Good Test
Taker
Exam
Grade
Diligent
Understands
HW
Grade
Use Bayes net-like inference algorithm
Desideratum #2:
Exploit Low-Level Structure
Causal independence (noisy-or)
x = f()
y = g()
z = x & flip(0.9) | y & flip(0.8)
Desideratum #2:
Exploit Low-Level Structure
Context-specific independence
x = f()
y = g()
z = case <x,y> of
<false,false> : flip 0.4
<false,true> : flip 0.6
<true> : flip 0.7
Desideratum #3:
Exploit Object Structure
Complex domain often consists of weakly
interacting objects
Objects share a small interface
Objects are conditionally independent given
interface
Student 1
Course Difficulty
Student 2
Desideratum #4:
Exploit Repetition
Domain often consists of many of the same
kinds of objects
Can inference be shared between them?
f() = complex
x1 = f()
x2 = f()
…
x100 = f()
Desideratum #5:
Use the Query
Only evaluate required parts of model
Can allow finite computation on infinite model
f() = f()
x = let y = f() in true
A query on x does not require f
Lazy evaluation is required
Particularly important for probabilistic languages,
e.g. stochastic grammars
Desideratum #6
Use Support
The support of a variable is the set of
values it can take with positive
probability
Knowing support of subexpressions can
simplify computation
f() = f()
x = false
y = if x then f() else true
Desideratum #7
Use Evidence
Evidence can restrict the possible values
of a variable
It can be used like support to simplify
computation
f() = f()
x = flip 0.6
y = if x then f() else true
observe x = false
Outline
Motivation
The IBAL Language
Inference Goals
Probabilistic Inference Algorithm
Lessons Learned
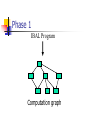
Two-Phase Inference
Phase 1: decide what computations
need to be performed
Phase 2: perform the computations
Natural Division of Labor
Responsibilities of phase 1:
utilizing query, support and evidence
taking advantage of repetition
Responsibilities of phase 2:
exploiting conditional independence, lowlevel structure and inter-object structure
Phase 1
IBAL Program
Computation graph
Computation Graph
Nodes are subexpressions
Edge from X to Y means “Y needs to be
computed in order to compute X”
Graph, not tree
different expressions may share subexpressions
memoization used to make sure each
subexpression occurs once in graph
Construction of
Computation Graph
1.
2.
Propagate evidence throughout
program
Compute support for each node
Evidence Propagation
Backwards and forwards
let x = <a:flip 0.4, b:1> in
observe x.a = true in
if x.a then ‘a else ‘b
Construction of
Computation Graph
Propagate evidence throughout
program
Compute support for each node
1.
2.
this is an evaluator for a nondeterministic programming language
•
•
•
lazy evaluation
memoization
Gotcha!
Laziness and memoization don’t go
together
Memoization: when a function is called,
look up arguments in cache
But with lazy evaluation, arguments are
not evaluated before function call!
Lazy Memoization
Speculatively evaluate function without
evaluating arguments
When argument is found to be needed
abort function evaluation
store in cache that argument is needed
evaluate the argument
speculatively evaluate function again
When function evaluates successfully
cache mapping from evaluated arguments to result
Lazy Memoization
let f(x,y,z) = if x then y else z
in f(true,’a,’b)
f(_,_,_)
Need x
f(true,_,_)
Need y
f(true,’a,_)
‘a
Phase 2
Computation Graph
Microfactors
Solution
P(Outcome=true)=0.6
Microfactors
Representation of function from
variables to reals
E.g.
X
False
False
True
Y
False
True
-
Value
0
1
1
is the indicator function of XvY
More compact than complete tables
Can represent low-level structure
Producing Microfactors
Goal: Translate an IBAL program into
a set of microfactors F
and a set of variables X
such that the P(Output) = f
X f F
Similar to Bayes net
Can solve by variable elimination
exploits independence
Producing Microfactors
Accomplished by recursive descent on
computation graph
Use production rules to translate each
expression type into microfactors
Introduce temporary variables where
necessary
Producing Microfactors
if e1 then e2 else e3
e1
e2
X
e1
X=True e2
X=False
X=True 1
e3
X=False e3
X=True 1
Phase 2
Computation Graph
Microfactors
Structured
Variable
Elimination
Solution
P(Outcome=true)=0.6
Learning and Decisions
Learning uses EM
Decision making uses backward
induction
like BNs, HMMs, SCFGs etc.
like influence diagrams
Memoization provides dynamic
programming
simulates value iteration for MDPs
Lessons Learned
Stochastic programming languages are
more complex than they appear
Single mechanism is insufficient for
inference in a complex language
Different approaches may each
contribute ideas to solution
Beware of unexpected interactions
Conclusion
IBAL is a very general language for
constructing probabilistic models
captures many existing frameworks, and allows
many new ones
Building an IBAL model = writing a
program describing how values are
generated
Probabilistic reasoning is like programming
Future Work
Approximate inference
loopy belief propagation
likelihood weighting
Markov chain Monte Carlo
special methods for IBAL?
Ease of use
Reading formatted data
Programming interface
Obtaining IBAL
www.eecs.harvard.edu/~avi/ibal