* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Special Angle Pairs Activity
Technical drawing wikipedia , lookup
Line (geometry) wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Rotation formalisms in three dimensions wikipedia , lookup
History of trigonometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Integer triangle wikipedia , lookup
Multilateration wikipedia , lookup
Trigonometric functions wikipedia , lookup
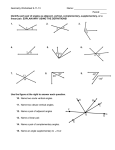
Special Angles Pre/Post-lesson Assessment Name: ________________________ I. For each of the following, indicate whether each pair are “Complementary Angles,” “Supplementary Angles,” “Vertical Angles,” and/or “Adjacent Angles.” Circle the correct answer(s). 80° 1 2 100° Complementary Angles Complementary Angles Supplementary Angles Supplementary Angles Vertical Angles Vertical Angles Adjacent Angles Adjacent Angles Linear Pair 45 1 45 2 Vertical Angles Vertical Angles Complementary Angles Complementary Angles Alternate Interior Angles Alternate Interior Angles Adjacent Angles Adjacent Angles Corresponding Angles Corresponding Angles 90° 1 90° 2 Complementary Angles Complementary Angles Supplementary Angles Supplementary Angles Vertical Angles Vertical Angles Adjacent Angles Adjacent Angles Linear Pair Linear Pair 45° 50° 45° 40° Complementary Angles Complementary Angles Supplementary Angles Supplementary Angles Vertical Angles Vertical Angles Adjacent Angles Adjacent Angles II. The measure of < 1 is x + 5, and the measure of < 2 is x – 9. A) Indicate whether < 1 and < 2 are “Complementary Angles,” “Supplementary Angles,” “Vertical Angles,” and/or “Adjacent Angles.” B) Find the value of x. C) Find the measure of < 1 and < 2 based on your value of x. III. Suppose <ABC is bisected by ray BD. The measure of <ABD is 6x – 22 , and the measure of < CBD is 2x + 34. A) Draw and label a diagram using the information above. B) Find the value of x. C) Find the measure of <ABD, <CBD, and <ABC. Special Angle Pairs Activity Materials Needed: Right triangle tessellated page (1/2 sheet is big enough) Copy of triangle on cardstock that matches the right triangle on the tessellated page (each angle is colored a different color) Wax paper or patty paper Colored pencils Directions: 1. Have students work in pairs to color the three angles of each triangle on the tessellated page to match the cardstock triangle. 2. Have students place patty paper over a portion of the tessellated page to find, draw, and write a description for each of the following concepts. a. b. c. d. e. f. 3. The sum of the angles in a triangle is 180 degrees. Vertical angles are congruent. If two parallel lines are cut by a transversal, corresponding angles are congruent. If two parallel lines are cut by a transversal, alternate interior angles are congruent. If two parallel lines are cut by a transversal, same side interior angles are supplementary. The sum of the angles in a linear pair is 180 degrees. Have students find other relationships that exist based on colors within the tessellated page. Examples include: 360 degrees in a rotation, 360 degrees in a quadrilateral, characteristics of congruent and similar triangles, complementary angles, and supplementary angles. Activity Extension: Tell if each statement is always, sometimes, or never true. Justify your reasoning. 1. Two angles that are complementary are also adjacent. 2. Vertical angles are also a linear pair. 3. Angles that form a linear pair are supplementary. 4. Alternate interior angles are congruent. 5. Same side interior angles are congruent. Solve each problem using the given diagrams. 6. 1 2 If the measure of < 1 is 3x + 2 and the measure of < 2 is 2x + 3, find the value of x. Find the measure of < 1 and < 2. Determine if the pair of angles are vertical, adjacent, complementary, supplementary, alternate interior, alternate exterior, corresponding, or if they form a linear pair. Justify your reasoning. 7. 1 2 If the measure of < 1 is 2x + 5 and the measure of < 2 is 3x – 15, then find the value of x. Find the measure of < 1 and < 2. Determine if the pair of angles are vertical, adjacent, complementary, supplementary, alternate interior, alternate exterior, corresponding, or if they form a linear pair. Justify your reasoning. Card-Sort Activity- Group the cards based on shared characteristics. Share with your partner how you decided to group them. Supplementa Complement Linear Pair ry ary Angles Angles Vertical Angles Two 45 degree Angles Two 90 degree angles Alternate Interior Same-Side Interior Alternate Exterior Correspond <1 and <5 ing Angles < 1 and the 76 degree < < 6 and <7 <4 and <6 <2 and the 130 degree < <2 and <1 <1 and <3 <2 and <D