* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 11_03 - Solving Systems of Equations by Graphing
Survey
Document related concepts
Transcript
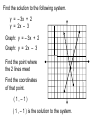
1) Graph y = 2x + 1 using slope & intercept 2) Graph x + 2y = 2 using x & y intercepts 2 The slope is 2 1 x intercept = 2 (2,0) y intercept is ( 0 , 1 ) y intercept = 1 (0,1) 11.03 Solving a System of Equations by Graphing Remember, a solution to a system of equations is an ordered pair ( x , y ) that make both equations true. One method for finding a solution to a system is using the graphing method. To solve a system of equations by graphing, graph each equation on the same coordinate plane and find the coordinates ( x , y ) of the point where the two lines meet. These coordinates ( x , y ) are the x and y values that are the solution to the system. Find the solution to the following system. y = – 3x + 2 y = 2x – 3 Graph: y = – 3x + 2 Graph: y = 2x – 3 Find the point where the 2 lines meet Find the coordinates of that point. (1,–1) ( 1 , – 1 ) is the solution to the system. Find the solution to the following system. x + y = 1 y = 2x + 4 Graph: x + y = 1 Graph: y = 2x + 4 Find the point where the 2 lines meet Find the coordinates of that point. (–1,2) ( – 1 , 2 ) is the solution to the system. Some systems do not have a solution. y = 3x – 2 y = 3x + 3 Graph: y = 3x – 2 Graph: y = 3x + 3 Find the point where the 2 lines meet The lines do not meet. They are parallel. What does this mean ? There is no solution to the system. Some systems have infinite solutions. 2x + 2y = 4 y = –x + 2 Graph: 2x + 2y = 4 Graph: y = – x + 2 Find the point where the 2 lines meet What two lines? They’re the same line. What does this mean ? There are infinite solutions, whatever numbers ( x , y ) work in the 1st equation will work in the 2nd. Try This: Find the solution to the following system. x + y = 4 y = 2x – 5 Graph: x + y = 4 Graph: y = 2x – 5 Find the point where the 2 lines meet Find the coordinates of that point. (3,1) ( 3 , 1 ) is the solution to the system.