Download RLC circuits

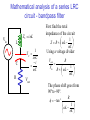
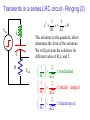
RLC circuits - Part 2
Resonance/Notches/Bandpass
Cartoon from Agilent, www.educatorscorner.com
Inductors - how do they work?
R
V0
dI
VL  L
dt
Start with no current in the circuit.
When the battery is connected, the
inductor is resistant to the flow of
L current. Gradually the current increases
to the fixed value V0/R, meaning that
the voltage across the inductor goes to
zero. In reality the inductor has a finite
resistance since it is a long wire so it
will then be more like a pair of series
resistances.
Inductors - time constant L/R
VR
V0
VL
Again the behavior of an inductor is seen
by analysis with Kirchoff’s laws.
Suppose we start with no current.
dI
V0  VR  VL  IR  L
dt
then I 
V0
R

 Rt 
1

exp

 L 


and
Rt 

 Rt 
VL  V0 exp   VR  V0 1  exp   
 L
 L 

There is a fundamental time scale set by L/R, which has units
of seconds (=Henry/Ohm)
RLC circuits with sinusoidal sources
The AC analysis of circuits with inductors is also easy, with the
effective resistance (impedance) of an inductor equal to iL.
From a phasor point of view this means that the inductor leads
the resistor by 90 degrees.
High pass and low pass filters can be made from inductors as
well. However the inductors are usually bulkier and relatively
expensive compared to capacitors (and more difficult to make in
an integrated circuit) so are not used as commonly.
Another limitation is that they are far from ideal. The impedance
is usually RL+iL, which means that in order to find the
breakpoint you use f = L/(2(RL+R)).
Notch and Bandpass
A filter can also serve to select or eliminate a narrow band of
frequencies. Examples are radio (select) and parental control
“channel eliminator” circuits.
Vout
Vout
Log10 f
Log10 f
Mathematical analysis of a series LRC
circuit - bandpass filter
Vin
Z L  iL
L
1
iC
i

C
ZC 
C
R
Vout
First find the total
impedance of the circuit
1 

Z  R  i  L 

C 

Using a voltage divider
Vout

Vin
R
1 

R  i  L 

C 

The phase shift goes from
90°to -90°.
   tan
1
R
1 


L



C 

Mathematical analysis of a series LRC
circuit - bandpass filter (2)
The magnitude of the gain, Av, is
Vin
Av 
L
C
R
Vout
Vout

Vin
R
1 

R 2   L 


C


2
Note that for high frequencies
L is dominant and the gain is
R/ L or small. At low
frequencies the gain is  RC
because the impedance of the
capacitor is dominant. At 2 =
1/LC the gain is one (assuming
ideal components).
Graphing for a series LRC circuit
RLC bandpass filter
1.2
f peak 
1
1
2 LC
Gain
0.8
0.6
0.4
0.2
0
0
2
4
Log10 Freq
6
Although the gain falls off
at 20 dB/decade at high and
low frequencies (this
means that it is
proportional to ) it is more
typical to plot it as shown
on a semi-log graph, since
this emphasizes the peak.
Q factor for a Series LRC circuit
RLC bandpass filter
1.2
1
Q
f 3dB
L

R LC
0.8
Gain
f peak
0.6
0.4
0.2
0
0
Solve
2
1

2
4
Log10 Freq
6
R
1 

R   L 

C 

2
2
The quality factor or Q is
defined as the energy
stored divided by the
energy loss/cycle. For an
electronic bandpass it is the
peak frequency divided by
the width of the peak or
bandwidth (defined by the
frequencies where the gain
is 3 dB lower than the
maximum).
f 3dB
R

L
Parallel LRC circuit
L
Z  Ri
 Ri
1 

1   2 LC 

 C 

L 

1
Vin
Vout
R

Vin R  i L
1   2 LC
C
R
Q
Vout
f peak
f 3dB
RC

LC
f valley 
1
2 LC
Av 
R
 L 
R2  

2
1


LC


Measured across the resistor, this
circuit is a notch filter, that is it
attenuates a small band of
frequencies. The bandwidth in this
case is defined by 3dB from the
lowest point on the graph.
2
Transients in a series LRC circuit - Ringing
Vin
L
C
R
Vout
Suppose instead of a sinusoidal source
we had a slowly varying square
waveform or a sharp turn on of
voltage. How would a LRC circuit
behave?
We can start by using Kirchoff’s
laws again.
dI Q
V0  VR  VL  VC  IR  L 
dt C
2
d Q dQ
Q
L 2 
R
dt
dt
C
This is a second order differential equation that can be solve
for the general and particular solutions.
Transients in a series LRC circuit - Ringing (2)
1
1
x 
x
0
RC
LC
The solutions to the quadratic above
determine the form of the solutions.
We will just state the solutions for
different value of R, L and C.
2
Vin
L
C
R
Vout
2
 1 
: Overdamped


LC
 RC 
2
 1 
: Critically damped


LC
 RC 
2
 1 
: Underdamp ed


LC
 RC 
Transients in a series LRC circuit - Ringing (3)
Vin
L
C
R
Vout
The last, underdamped, results in an
exponentially decaying envelope and a
sinusoidal oscillations. This ringing is
commonly observed. It can be thought of as
two parts: a loss of energy related to R and
an oscillation related to the product LC.
This not exact so lets look at the
mathematical solution.
 1
1 
t 

VR (t )  K1 cos 
 2 2 t  exp 

LC
4
R
C
2
RC



When (RC)2>>LC the cos will oscillate several times at a
frequency almost equal to the resonant frequency.