Download 1.1 Rectangular Coordinates 1.1rect_coord

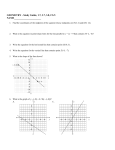
Objectives:
1. To do all kinds of
things with points in
the Cartesian plane:
scatter plot,
distance, midpoint,
slope, equation
2. To solve an equation
for a particular
variable
 As a class, use your
vast mathematical
knowledge to define
each of these words
without the aid of
your textbook.
Rectangular
Coordinates
Cartesian Plane
Origin
Quadrants
Ordered Pair
Scatter Plot
Pythagorean
Theorem
Midpoint
Slope
Linear Equation
The Cartesian Coordinate
Plane is a flat place where
points hang out
 Usually called a “graph”
 Uses ordered pairs of real
numbers to locate points
 Gives a visual
representation of the
relationship between x
and y
(Also called a Rectangular Coordinate System)




1596-1650
French philosopher-etc.
Cogito Ergo Sum
A fly taught him about
the Cartesian
coordinate plane and
analytic geometry, for
which he took full credit
Use your calculator to draw a scatter plot of the
following data. Then find the line of best fit.
x
0
1
2
3
4
5
6
7
8
y
1
3
6
8
4
5
7
8
10
From 1990 through
2003, the amounts A
(in millions of dollars)
spent on skiing
equipment in the
United States are
shown in the table,
where t represents
the year. Sketch a
scatter plot of the
data.
Year, t
Amount, A
1990
475
1991
577
1992
521
1993
569
1994
609
1995
562
1996
707
1997
723
1998
718
1999
648
In a right triangle, the
square of the length of
the hypotenuse is equal
to the sum of the
squares of the lengths of
the legs.
c2
a2
b2
If the coordinates of
points A and B are
(x1, y1) and (x2, y2),
then
AB 
x2  x1 2   y2  y1 2
To the nearest hundredth of a unit, what is the
approximate length of RS, with endpoints
R(3, 1) and S(-1, -5)?
The distance between (-4, k) and (4,4) is 10
units. Find the value of k.
If A(x1,y1) and B(x2,y2)
are points in a
coordinate plane,
then the midpoint M
of AB has coordinates
 x1  x2 y1  y2 
,


2 
 2
Find the midpoint of the segment with
endpoints at (-1, 5) and (3, 3).
The midpoint C of IN has coordinates (4, -3).
Find the coordinates of point I if point N is at
(10, 2).
Slope can be used to represent an average rate
of change.
 A rate of change is how much one quantity
changes (on average) relative to another.
 For slope, we measure how y changes relative
to x.
The slope m of a
nonvertical line is the
ratio of vertical
change (the rise) to
the horizontal change
(the run).
Find the slope of the line passing through the
points (-4, -5) and (6, -2).
Find the value of k such that the line passing
through the points (-4, 2k) and (k, -5) has
slope -1.
A linear function can have many forms, pick
your favorite:
 Slope-Intercept Form: y  mx  b
 Point-Slope Form: y  y1  m  x  x1 
 Standard Form: Ax  By  C
Write the equation of the line through the
points (-2, 5) and (4, -7). Write your answer in
point-slope, slope-intercept, and standard
forms.
Page 7 of your book contains these helpful
formulas. Number them thusly:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Given any of the previous formulas, what would
it mean to solve for a particular variable?
To solve for a variable in an equation or formula
means to isolate that variable on only one side
of the equation:
variable = everything else
Solve V = (4/3)r3 for r.
Objectives:
1. To do all kinds of
things with points in
the Cartesian plane:
scatter plot,
distance, midpoint,
slope, equation
2. To solve an equation
for a particular
variable