* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Heat As Energy Transfer Problem
Geothermal energy wikipedia , lookup
Internal energy wikipedia , lookup
Solar thermal energy wikipedia , lookup
Conservation of energy wikipedia , lookup
Solar water heating wikipedia , lookup
Energy applications of nanotechnology wikipedia , lookup
Environmental impact of electricity generation wikipedia , lookup
Heat exchanger wikipedia , lookup
Geothermal heat pump wikipedia , lookup
Compressed air energy storage wikipedia , lookup
Solar air conditioning wikipedia , lookup
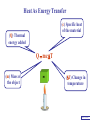
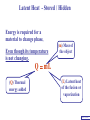
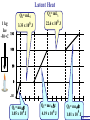
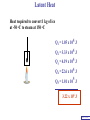
Heat Physics Lecture Notes Heat 14 (01 of 32) Heat 1) Heat As Energy Transfer 2) Internal Energy 3) Specific Heat 4) Calorimetry 5) Latent Heat 6) Heat Transfer: Conduction Heat 14 (02 of 32) Heat As Energy Transfer Heat is random thermal Energy Unit of heat: calorie (cal) 1 cal is the amount of heat necessary to raise the temperature of 1 g of water by 1 Celsius degree. 1 kcal is the amount of heat necessary to raise the temperature of 1 kg of water by 1 Celsius degree. Heat 14 (13 of 32) Heat As Energy Transfer Heat is a form of energy and can be equated to mechanical energy. The apparatus below is used to determine the mechanical equivalent of heat: 4 .186 J 1 cal 4186 J 1 kcal Heat 14 (13 of 32) Heat As Energy Transfer Definition of heat: Heat is thermal energy transferred from one object to another because of a difference in temperature. The sum total of all the energy of all the molecules in a substance is its internal (or thermal) energy. Temperature: measures molecules’ average kinetic energy Internal energy: total energy of all molecules Heat: transfer of energy due to difference in temperature Heat 14 (13 of 32) Heat As Energy Transfer (c) Specific heat of the material (Q) Thermal energy added Q mc T (m) Mass of the object m (T) Change in temperature Heat 14 (13 of 32) Chapter 14 Page 387 Heat 14 (13 of 32) Heat As Energy Transfer Problem: A 50 g piece of cadmium is at 20 oC. If 400 J of heat is added to the cadmium, what is its final temperature J ccadmium 230 kg Co Q mc T Q T mc 400 J 0.050 kg 230 J kg Co 34.8 C o Tf To T Tf 20 .0 o C 34 .8 C o 54.8 o C Heat 14 (13 of 32) Heat As Energy Transfer Problem: A 100 g lead bullet traveling at 300 m/s is stopped by a large tree. Half the kinetic energy of the bullet is transformed into heat energy and remains with the the bullet while the other half is transmitted to the tree. What is the increase in temperature of the bullet? J c lead 130 o kg C ΔK bullet Q bullet 2 mv 2 mcT 4 2 v T 4c 300 m/s 2 4 130 J o 173 C o kg C Heat 14 (13 of 32) Heat As Energy Transfer Problem: A 3.0 kg block of iron is dropped from rest from the top of a cliff. When the block hits the ground it is observed that its temperature increases by 0.50 oC. Assume that all the potential energy is used to heat the block. How high is the cliff? J c iron 450 kg Co U block Q block mgh mc T cT h g J 450 0.50o C kg Co 9.8 m/s 2 23 m Heat 14 (13 of 32) Heat As Energy Transfer Problem: A 1.5 kg copper block is given an initial speed of 30 m/s on a rough horizontal surface Because of friction, the block finally comes to rest. If the block absorbs 85% of its initial kinetic energy in the form of heat, Calculate its increase in temperature? J ccopper 390 o kg C Q block 0.85 K block mv 2 mcT 0.85 2 v2 T 0.85 2c 30 m/s 2 0.85 2 390 J 1 .0 o C kg Co Heat 14 (13 of 32) Calorimetry Problem: A 0.40 kg iron horseshoe that is initially at 500 oC is dropped into a bucket containing 20 kg of water at 22 oC. What is the final equilibrium temperature? Neglect any heat transfer to for from the surroundings. Q gain Q loss m W c W Δ TW m I c I Δ TI 20 4186 Tf J c iron 450 kg Co J c water 4186 kg Co 22 0 .4 450 500 Tf 83720Tf 1841840 90000 180 Tf Tf 23 o C Heat 14 (13 of 32) Calorimetry Problem: A 200 g block of copper at a temperature of 90 oC is dropped into 400 g of water at 27 oC. The water is contained in a 300 g glass container. What is the final temperature of the mixture J kg Co J c water 4186 kg Co J c glass 840 kg Co ccopper 390 Q gain Q loss m W c W Δ TW m G c G Δ TG m C c C Δ TC 0.4 4186 Tf 27 0 .3 840 Tf 27 0 .2 390 90 Tf 1674 .4 Tf 45208 252 Tf 6804 7020 78 Tf Tf 29 .5 o C Heat 14 (13 of 32) Example 1: A 500-g copper coffee mug is filled with 200-g of coffee. How much heat was required to heat cup and coffee from 20 to 960C? 1. Draw sketch of problem. 2. List given information. Mug mass mm = 0.500 kg Coffee mass mc = 0.200 kg Initial temperature of coffee and mug: t0 = 200C Final temperature of coffee and mug: tf = 960C 3. List what is to be Total heat to raise temperature found: of coffee (water) and mug to 960C. Example 1(Cont.): How much heat needed to heat cup and coffee from 20 to 960C? mm = 0.2 kg; mw = 0.5 kg. 4. Recall applicable formula or law: Heat Gain or Loss: Q = mc t 5. Decide that TOTAL heat is that required to raise temperature of mug and water (coffee). Write equation. QT = mmcm t + mwcw t 6. Look up specific Copper: cm = 390 J/kg C0 heats in tables: Coffee (water): cw = 4186 J/kg C0 Example 1(Cont.): How much heat needed to heat cup and coffee from 20 to 960C? mc = 0.2 kg; mw = 0.5 kg. 7. Substitute info / solve problem: Copper: cm = 390 J/kg C0 Coffee (water): cw = 4186 J/kg C0 QT = mmcm t + mwcw t Water: (0.20 kg)(4186 J/kgC0)(76 t = 960C - 200C 0 C) 0 = 76 C Cup: (0.50 kg)(390 J/kgC0)(76 C0) QT = 78.4 QT = 63,600 J + 14,800 J kJ Calorimetry m1 TH Q loss m2 TL Q gain Conservation of thermal energy: Q gain Q loss m 2 c 2 Δ T2 m 1c1Δ T1 m 2 c 2 Tf TL m 1c1 TH Tf Final Temperature: m1c1TH m 2c 2 TL Tf m1c1 m 2c 2 Heat 14 (13 of 32) Latent Heat - Stored / Hidden Energy is required for a material to change phase, Even though its temperature is not changing. (m) Mass of the object Q mL (Q) Thermal energy added (L) Latent heat of the fusion or vaporization Heat 14 (13 of 32) The water problem Table of latent heats The following table shows the latent heats and change of phase temperatures of some common fluids and gases. Substance Latent Heat Fusion kJ/kg Melting Point °C Latent Heat Vaporization kJ/kg Boiling Point °C Alcohol, ethyl 108 −114 855 78.3 Ammonia 339 −75 1369 −33.34 Carbon dioxide 184 −78 574 −57 21 −268.93 Helium Hydrogen(2) 58 −259 455 −253 Lead[8] 24.5 327.5 871 1750 Nitrogen 25.7 −210 200 −196 Oxygen 13.9 −219 213 −183 R134a −101 215.9 −26.6 Toluene −93 351 110.6 Turpentine Water 293 334 0 2260 100 Latent Heat Heat of fusion, Lf: heat required to change 1.0 kg of material from solid to liquid Heat of vaporization, Lv: heat required to change 1.0 kg of material from liquid to vapor Chapter 14 - Page 392 Heat 14 (13 of 32) Latent Heat 1 kg Ice -50 oC Q2= mLf Q4= mLv 3.33 x 105 J 22.6 x 105 J 150 100 50 0 50 Q1= mcIt 1.05 x 105 J Q3= mcWt Q5= mcSt 4.19 x 105 J 1.01 x 105 J Heat 14 (13 of 32) Latent Heat Heat required to convert 1 kg of ice at -50 oC to steam at 150 oC Q1 = 1.05 x 105 J Q2 = 3.33 x 105 J Q3 = 4.19 x 105 J Q4 = 22.6 x 105 J Q5 = 1.01 x 105 J 3.22 x 106 J Heat 14 (13 of 32) Latent Heat Problem: A large block of ice at 0 oC has a hole chipped in it, and 400 g of aluminum pellets at a temperature of 30 oC are poured into the hole. How much of the ice melts? Q ( gain ) Q loss m I L f m A c A TA J caluminum 900 kg Co kJ L f water 333 kg Co m A c A TA mI Lf J 0.4 kg 900 0 30 Co kg Co mI J 5 3.33 x 10 kg 0.032 kg Heat 14 (13 of 32) Conduction Heat conduction can be visualized as occurring through molecular collisions. x The heat flow per unit time is given by: Q kAT1 T2 t x Heat 14 (13 of 32) Conduction The constant k is called the thermal conductivity. Materials with large k are called conductors; those with small k are called insulators. Chapter 14 Page 396 Heat 14 (13 of 32) Conduction Problem: A window has a glass surface of 1.6 x 103 cm2 and a thickness of 3.0 mm. Find the rate of heat transfer by conduction through this pane when the temperature of the inside surface of the glass is 20 oC and the outside temperature is 40 oC. J k glass 0.84 s m Co Q kAT t x 2 W 1 m 0.84 1.6 x 10 3 cm 2 20 oC oC 100 cm m 3.0 x 10 3 m ΔQ 896 J / s Δt Heat 14 (13 of 32) Conduction Problem: A glass window pane has an area of 3.0 m2 and a thickness of 0.60 cm. If the temperature difference between its faces is 25 oC, how much heat flows through the window per hour? J k glass 0.84 o s m C Q kAT t x W 0.84 3 m 2 25 Co 3600 s kAT t m Co Q 0.006 m x ΔQ 3.78 x 10 7 J Heat 14 (13 of 32) Conduction Building materials are measured using R−values rather than thermal conductivity: L R k Where, L is the thickness of the material. Chapter 14 Page 397 Heat 14 (13 of 32) Summary Internal energy U refers to the total energy of all molecules in an object. For an ideal monatomic gas, U 3 NkT 3 nRT 2 2 Heat is the transfer of energy from one object to another due to a temperature difference. Heat can be measured in joules or in calories. Q mcΔ T Specific heat of a substance is the energy required to change the temperature of a fixed amount of matter by 1° C. Heat 14 (13 of 32) Summary In an isolated system, heat gained by one part of the system must be lost by another. Calorimetry measures heat exchange quantitatively. Energy in involved in phase changes even though the temperature does not change. Heat of fusion: amount of energy required to melt 1 kg of material. Heat of vaporization: amount of energy required to change 1 kg of material from liquid to vapor. Q mL Heat 14 (13 of 32) Summary Heat transfer takes place by conduction, convection, and radiation. In conduction, energy is transferred through the collisions of molecules in the substance. Q kAT t x Heat 14 (13 of 32) Internal Energy Internal energy of an ideal (monatomic) gas: 2 U N 1 mv2 kinetic energy in terms of the temperature 1 mv2 2 3 kT 2 NkT nRT U 3 NkT 2 U 3 nRT 2 Heat 14 (13 of 32)