Download Geometry-13-17 January 2013 -polygon - Shope-Math

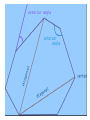
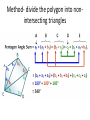
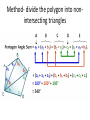
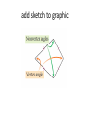
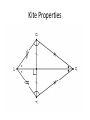
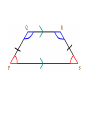
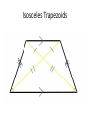
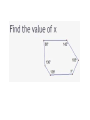
Geometry 13 January 2014
Warm Up- (keep pink sheets in left side )
1) Correct Homework
a) Work with your group to IDENTIFY and
CORRECT ERRORS. √ or X EACH PROBLEM.
b) Please do MORE than just write the ‘correct’
answer…. HOW do you get it!!?
Show the WORK to SUPPORT the correct answer!
2) Do #11 Flowchart Proof HANDOUT
objective
Students will develop, prove and apply polygon
interior and exterior sum conjectures.
Students will take notes, work collaboratively
and present to the class.
Homework:
DUE TODAY: pg. 259+: 3 – 10
Start with sketch. Clearly show K’s and W’s.
CHECK YOUR ANSWERS.
DUE SUNDAY/ Monday- KHAN ASSIGNMENT
DUE FRIDAY, January 17:
pg. 264: 7, 8, 10, 16
pg. 271: 1 – 8
FINISH 5.2 HANDOUT (both sides)
Write in your Notes
1)EXPLAIN in writing
THINK-PAIR- SHARE
WHAT are THREE DIFFERENT METHODS that
could be used to find the interior angle sum of
any polygon?
2) USE at least 2 different methods to find the
missing interior angle sum of a hexagon. Clearly
show your thinking.
Method- divide the polygon into nonintersecting triangles
Method- triangles with common
vertex somewhere inside polygon
Interior angle sum = 180n - 360
Method- develop/use the rule
Polygons
Term
Definition
Polygon
Sum
Conjecture
The sum of the measures of
the interior angles of an
n-gon is
Exterior
angle sum
conjecture
For any polygon, the
sum of the measures of
a set of external angles
is 3600
Equiangular
Polygon
Conjecture
Each interior angle of an
equiangular n-gon
1800  n  2 
1800  n  2 
n
Example
Sum of interior
angles
1800  n  2 
1800  n  2 
n
Prove Exterior Angle Sum
https://www.youtube.com/watch?v=btfso-DF2gkPROOF
https://www.youtube.com/watch?v=004BlxN06gg
Algebraic Proof
Practice
Do PROOF- two methods- HANDOUT
Start with words… divide the polygon into…..
KHAN QUIZ– when finished you may begin work on:
Do Lesson 5.2 Handout (finish for homework)
Be ready to share your work with the class.
Practice- Angle Chase, #12
Calculate the measure of each lettered angle
measure. Explain how you found your answer.
Show brief calculation and relationship.
Triangle Sum: a + b + 34 = 180
Quadrilateral Sum, LP, VA, CA, etc.
Be ready to share a PART of the puzzle with the
class!!
Debrief
What different methods can you use
to find the interior angle sum of any
polygon?
What is the exterior angle sum for any
polygon?
Geometry
14 January 2014
Warm Up
DO Four Pentagons Handout
Please work independently
We will discuss your work with a partner
later in the week.
objective
Students will develop, prove and apply polygon
interior and exterior sum conjectures.
Students will take notes, work collaboratively
and present to the class.
DUE FRIDAY, January 17:
pg. 264: 7, 8, 10, 16
pg. 271: 1 – 8
FINISH 5.2 HANDOUT (both sides)
NO SCHOOL next Monday, January 20
DUE Monday/ Tuesday- KHAN ASSIGNMENT
Method- divide the polygon into nonintersecting triangles
Method- triangles with common
vertex somewhere inside polygon
Interior angle sum = 180n - 360
Method- develop/use the rule
Polygons
Term
Definition
Polygon
Sum
Conjecture
The sum of the measures of
the interior angles of an
n-gon is
Exterior
angle sum
conjecture
For any polygon, the
sum of the measures of
a set of external angles
is 3600
Equiangular
Polygon
Conjecture
Each interior angle of an
equiangular n-gon
1800  n  2 
1800  n  2 
n
Example
Sum of interior
angles
1800  n  2 
1800  n  2 
n
Practice- Angle Chase, #12
Calculate the measure of each lettered angle
measure. Explain how you found your answer.
Show brief calculation and relationship.
Triangle Sum: a + b + 34 = 180
Quadrilateral Sum, LP, VA, CA, etc.
Be ready to share a PART of the puzzle with the
class!!
Practice
Do Lesson 5.2 Handout – BOTH SIDES
(finish for homework)
Be ready to share your work with the class.
Debrief
How can you find the measures of interior
angles of regular polygons if no measures are
given?
Geometry 15/16 January
WARM UP
1) Do work on finding angle measures on handout
2) FINISHED? WORK ON 5.2 handoutfocus #7
QUESTIONS?
objective
Students will explore properties of kites and
trapezoids.
Students will take notes, work collaboratively
and present to the class.
DUE FRIDAY, January 17:
pg. 264: 7, 8, 10, 16
pg. 271: 1 – 8
FINISH 5.2 HANDOUT (both sides)
NO SCHOOL next Monday, January 20
DUE Monday/ Tuesday- KHAN ASSIGNMENT
Syllabus
REVIEW briefly– homework policy
late work policy
BRING BACK signed pink slip for 8 easy
homework points---- I’ll accept them through
Friday, Jan 24
Summarizing Properties of Quadrilaterals
Quadrilateral
Kite
Parallelogram Trapezoid
Isosceles Trapezoid
Rhombus
Rectangle
Square
Review Quadrilateral DEFINITIONS
Use graphic organizer.
WRITE definitions for each quadrilateral.
MARK each figure with notation showing the
definition.
Is a cow ALWAYS a mammal?
Is a mammal ALWAYS a cow?
A square (ALWAYS, SOMETIMES, NEVER)
a parallelogram.
A parallelogram (ALWAYS, SOMETIMES, NEVER)
a square.
examples:
1) A kite is ALWAYS a __________________.
2) A parallelogram is SOMETIMES a ______________.
3) A square is ALWAYS a _____________.
4) A rectangle is ______________a square.
Geometry Properties of Polygons
see page 268– read together
add sketch to graphic
Using properties of kites
• A kite is a quadrilateral
that has two pairs of
consecutive congruent
sides, but opposite
sides are not congruent.
What about kites?
Are there any relationships with the angles?
Are any congruent?
What about the diagonals? Do they bisect each
other? Do they
Bisect angles?
read about trapezoids- pg. 269
read together
Using properties of trapezoids
• A trapezoid is a
quadrilateral with
exactly one pair of
parallel sides.
A
base
leg
leg
D
B
base
C
special quadrilaterals- see pg. 64+
Trapezoid: a quadrilateral with exactly one pair
of parallel sides
Isosceles Trapezoid: a trapezoid with nonparallel sides congruent
What about trapezoids?
Are any angles the same measure?
What about isosceles trapezoids? Angles?
Do you notice anything with the diagonals.
What relationships can you find?
Investigations pg. 268-270
Fill in your graphic organizer as we do the patty
paper investigations on polygon properties.
All students will do the investigations in sections 5.3 –
5.6, summarizing your conjectures with sketches and
related vocabulary on the handout.
Expectations- do your work on a separate paper/ patty
paper and attach to the handout. Label each paper
with page and investigation title.
THINK- PAIR-SHARE
THINK- LIST all the congruencies and properties
you can find that are true with your
KITE
EXAMPLE- segmentKT bisects angle EKI
PAIR- work with a partner to add to list
GROUP– who found the most? +1 cw point
Kite Properties
Isosceles Trapezoids
Debrief
Is a kite always a
quadrilateral?
What special properties
does a kite have?
Is a quadrilateral always a
kite?
What about a trapezoid?
Geometry
17 January 2014
1) CHECK homework √ or X each problem
DUE TODAY, January 17:
pg. 264: 7, 8, 10, 16
pg. 271: 1 – 8
FINISH 5.2 HANDOUT (both sides)
Work with a partner to identify and CORRECT your
work to support the correct answer
2) Done? Sketch a kite and an isosceles trapezoid.
MARK all you know to be true on the diagram (congruent
parts? 90⁰? Bisect?)
Objective
Students will show understanding of polygon
sums and kite/ trapezoid properties on a quiz.
NO SCHOOL next Monday, January 20
DUE Monday/ Tuesday- KHAN ASSIGNMENT
notes on videos
exercises
Polygons
Term
Definition
Polygon
Sum
Conjecture
The sum of the measures of
the interior angles of an
n-gon is
Exterior
angle sum
conjecture
For any polygon, the
sum of the measures of
a set of external angles
is 3600
Equiangular
Polygon
Conjecture
Each interior angle of an
equiangular n-gon
1800  n  2 
1800  n  2 
n
Example
Sum of interior
angles
1800  n  2 
1800  n  2 
n
QUIZ
Do you best.
Work silently.
FINISHED?
Begin to work on the
PROOF handout.