Download Stellar Evolution

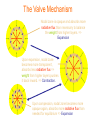
Pulsating Variables
Cepheid Variables
Discovered by J. Goodricke (1784):
Prototype:
d Cephei
Light curve of d Cephei
Cepheid Variables:
The Period-Luminosity Relation
The variability period P of a Cepheid variable is
positively correlated with its luminosity:
MV = -2.80 log10Pd – 1.43
Cepheid Variables
as Distance Indicators
Measuring a Cepheid’s period
 determine its absolute magnitude
 Distance
indicator!
Cepheids are Ib supergiants, L ~ 103 - 4 L0
=> Identifiable out to several Mpc!
The Instability Strip
Classical
Cepheids
W Virginis Stars:
metal-deficient
(Pop. II),
Cepheid-like
d Scuti Stars:
Evolved F stars
near MS
RR Lyrae Stars: Pop. II;
horizontal-branch;
nearly standard-candle
luminosity!
Increasing
Period
Stellar
Pulsations
Estimate from sound travel
time through the star:
P ~ r-1/2
Cepheids all have approx.
the same surface
temperature.
=> Higher L => Larger R
=> Smaller r => Larger P
Radial Pulsations
The Valve Mechanism
Nodal zone is opaque and absorbs more
radiative flux than necessary to balance
the weight from higher layers. =>
Expansion
Upon expansion, nodal zone
becomes more transparent,
absorbs less radiative flux =>
weight from higher layers pushes
it back inward. => Contraction.
Upon compession, nodal zone becomes more
opaque again, absorbs more radiative flux than
needed for equilibrium => Expansion
For the valve mechanism to work:
k needs to increase with increasing r and T
log(aR [cm-1])
Kramer’s Opacity Law
Gas
gradually
becoming
ionized
aR ~ r T-7/2
Gas fully ionized;
opacity dominated
by free-free
absorption
104
105
106
107
Temperature [K]
→ Partial Ionization Zones!
Location of Partial Ionization Zones
LPVs:
Valve mechanism driven by
H partial ionization zones
~ 104 K
~ 4x104 K
Instability strip:
Walve mechanism driven by
He partial ionization zones
Non-Radial Modes of Variability:
g-modes:
fnet = (dF/dV)net =
g (rs – rb)
bubble (‘b’)
surrounding
medium (‘s’)