* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Up and Down the Scale
Tone cluster wikipedia , lookup
Traditional sub-Saharan African harmony wikipedia , lookup
Chichewa tones wikipedia , lookup
Tone (linguistics) wikipedia , lookup
Consonance and dissonance wikipedia , lookup
Luganda tones wikipedia , lookup
Circle of fifths wikipedia , lookup
Mode (music) wikipedia , lookup
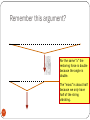
Microtonal music wikipedia , lookup
Equal temperament wikipedia , lookup
Set 7 What’s that scale?? 1 Note Grades should be available on some computer somewhere. The numbers are based on the total number of correct answers, so 100% = 30. When I review the numbers, this may change. We will get your individual results to you shortly .. Be forgiving, I don’t have the foggiest idea how to do this stuff yet. Now .. Back to music. 2 Remember Helmholtz’s Results Note from Middle C C D E Frequency 264 297 330 F G A B 352 396 440 496 3 Today Look at how this scale developed. It is mostly arithmetic. This material is in Measured Tones. Readings: Chapter 1 pages 1-11 o Read pages 12-16 for the “flavor” o Chapter 2 – All: 17-36 Don’t worry about the musical notation. Today is a religious holiday for many, so no clickers. 4 Last time we messed with this stuff. Tone Compare the results From these two sources. 5 Violin 6 The Violin L We will make some measurements based On these lengths. 7 Play an octave on one string • Volunteer to watch where the finger winds up on the finger board. • Measure the length of the string. • How close is it to ½ the length? 8 Let’s Listen to the Violin 1) Let’s listen to the instrument, this time a real one. 9 The parts One tone alone .. E on A string E on the E string Both together (the same?) A Fifth A+E open strings Consecutive pairs of fifths – open strings. A second? Third? Fourth? Seventh? The ratios of these lengths Should be ratios of integers If the two strings, when struck At the same time, should sound “good” together. 10 Remember this argument? For the same “x” the restoring force is double because the angle is double. The “mass” is about half because we only have half of the string vibrating. 11 Pythagoras Noticed that the sound of half of a string played against the sound of a second full string, both with the same original tone, sounded well together. This was called the octave (we discussed this last time). He then noticed that a very melodious tone also came when the string was divided into 1/3 – 2/3. When the larger portion of the string was played against the original length, it was called the fifth. In particular, the tone was “a fifth above the original tone”. 12 For the same “x” the restoring force is double because the angle is double. So… F kx 1 f 2 k m The “mass” is about half because we only have half of the string vibrating. k doubles m -> m/2 f doubles! 13 1 f 2 1 2 2f k 1 m 2 4k 1 m 2 2k m/2 k 4 m Octave 1 0.5 f 0.001 0.002 0.003 0.004 0.005 0.001 0.002 0.003 0.004 0.005 0.001 0.002 0.003 0.004 0.005 -0.5 -1 1 0.5 2f -0.5 -1 1.5 1 0.5 SUM -0.5 -1 -1.5 14 The sum has the same basic periodicity as The original tone. Sounds the “same” Time The keyboard – a reference The Octave Next Octave Sounds the “same” 15 Middle C The Octave 12 tones per octave. Why 12? … soon. Played sequentially, one hears the “chromatic” scale. Each tone is separated by a “semitione” Also “half tone” or “half step”. Whole Tone = 2 semitones 16 Properties of the octave Two tones, one octave apart, sound well when played together. In fact, they almost sound like the same note! A tone one octave higher than another tone, has double its frequency. Other combinations of tones that sound well have frequency ratios that are ratios of whole numbers (integers). It was believed olden times, that this last property makes music “perfect” and was therefore a gift from the gods, not to be screwed with. This allowed Pythagoras to create and understand the musical scale. 17 The Octave As we determine the appropriate notes in a scale, we will make use of the fact that two tones an octave apart are equivalent. We can therefore determine all of the equivalent tones by doubling or halving the frequency. This process is used to build up the scale. 18 f 200 Hz 1 T sec 200 f 300 Hz 1 T sec 300 19 Part II Scaling the Scale 20 Calendar The next examination will be on Friday, October 17th. This is a one session delay from what is announced in the syllabus. Today we continue building the scale. Then we return to the textbook to talk about energy, momentum and some properties of gas (our atmosphere) so we can deal with exactly what sound waves are. Let’s do a quick clicker review of the last class. 21 READING ASSIGNMENT Textbook pp 313-320 324-325 (beats) Measured Tones Chapter 4 – pp 86-97 22 Fifth C f G C 1.5f 2f A fifth is a span of 5 whole tones on the piano. It also spans 7 semitones. 23 Let’s look at the “fifth” Formed with 2/3 of the original length. Considered to be a “perfect” sound because of the small number ratio in lengths. We can form many of the notes of a scale using this ratio. The scale so formed sounds great but has problems. 2/3 L m=2/3 M (smaller) k=3/2 K 24 (larger) The Perfect Fifth … Sounds Good! f2/3 1 2 (3 / 2)k 1 (2 / 3)m 2 (3 3)k 3 f2/3 (2 2)m 2 f 2 / 3 1.5 f frequency f 25 1.5f fifth 2f Octave Other Fifths – also pretty good! Beethoven’s Fifth 26 C G C 5 1 2 3 The Intervals: 1 2 3 4 fifth f 4 fourth 1.5f 2f The fifth is 7 semitones above the fundamental tone, f. Since f and 2f are an octave apart, the interval from G to C should also be melodic. This interval consists of five (5) semitones. This “special interval” is referred to as a FOURTH. Let’s see how much of a scale we can create using these two musical intervals. 27 F kx 1/4 3/4 1 f 2 k m reference 1 f fourth 2 (4 / 3)k 1 (3 / 4)m 2 16k 4 f0 9m 3 This is a nice ratio of small integers that will also harmonize with the cosmos. 28 OK … Let’s build a scale! 29 Pythagorean Fifths Scaling the Scale C f G 1.5f We start with Middle C at frequency f (264 Hz ) We will actually add the numbers later. First tone is a fifth: 1.5f G Last tone is the octave: 2fC above Middle C. 30 C 2f P’s 5 Ratio 1/1 4/3 3/2 2/1 Decimal 1.000 1.3333 1.5000 2.000 Question: Are there any other intervals between 1f and 2f that correspond to singable intervals? Pythagoras Rule: Take an existing ratio. Multiply by 1.5 to get a fifth above the ratio. If the number is greater than 2, reduce it by an octave (divide by 2) If the number is less than 1, increase it by an octave by doubling the number. 31 Another tone: 3 3 9 2.25 2 2 4 Too Big! Divide by 2 9 1.125 8 32 More of the same … 3 3 3 27 2 2 2 8 Too Big 27 1 27 1.688 8 2 16 33 So Far 34 From C Ratio Frequency 264 1.000 264 1.125 297 1.333 353.3 1.500 396 1.688 445.6 2.000 528 C D E F G A B We could start with the A below middle C and get the 440 right. 264 297 330 352 396 440 496 Tones together We discussed that a scale should be made up of tones that sound well together. Even for a scale that is put together as we have just done, some tones will sound a bit bad together; but not terrible. Let’s see why some of the better combinations sound well. 35 The original sound A:440 Hz. 1 0.5 0.005 -0.5 -1 36 0.01 0.015 0.02 time The Octave: 440 + 880 1.5 1 0.5 0.005 0.01 0.015 0.02 -0.5 -1 -1.5 A PERIODIC sound and our brains accept this as a “nice” tone. 37 The fifth 1.5 1 0.5 0.005 -0.5 -1 -1.5 38 0.01 0.015 0.02 The Third 1.125 f0 2 1 0.005 -1 -2 39 0.01 0.015 0.02 Longer period of time 2 1 0.02 -1 -2 40 0.04 0.06 0.08 A New Phenomenon T~0.0195 seconds estimate 2 1 0.02 -1 -2 41 T 0.0195 sec 1 f 51 Hz T f 0 440 Hz f1 440 1.125 495 Hz f1 f 0 55 Hz 1 1 T 0.018 sec f 55 42 This phenomenon is called BEATS 2 1 0.02 0.04 0.06 -1 -2 43 The beat frequency between two similar frequencies is found to be the difference between the frequencies 0.08 Min 44 Max 45 Beats Low beat frequencies (1-20 Hz) can be heard and recognized. Faster beat frequencies can be annoying. Two frequencies an octave apart but off by a few Hz. will also display beats (difference between the frequencies as well) but they are harder to hear and somewhat unpleasant to the ear. 46 Problems The system of fifths to generate a scale works fairly well BUT if you start on a different note (F instead of C), the frequencies of the same notes will differ by a slight amount. this means that an instrument usually must be tuned for a particular starting mote (key). Modulation doesn’t work well. One interesting problem is the octave over a large range. 47 The Octave Problem Seven octaves represents a frequency range of 27=128 The same distance is covered by 12 fifths: (3/2)12=129.75 Some people can hear this difference … a problem, Many other tones wind up being slightly different. 48 Problems.. You can create scales using different sets of “primitive” combinations … thirds, sixths. Each yields a specific scale. They are not the same (read chapter 1 in MT). One can’t change “keys” easily using these schemes. Something had to be done. Solution: Equal Tempered Scales. The frequency difference between two consecutive semitones is set to be: 49 12 2 Keeps the octave exactly correct Screws up all of the other intervals ◦ But we can’t easily hear the difference One tuning will work for all keys 50 (fourths, fifths and sixths) Interval Ratio to Fundamental Just Scale Ratio to Fundamental Equal Temperament Unison 1.0000 1.0000 Minor Second 25/24 = 1.0417 1.05946 Major Second 9/8 = 1.1250 1.12246 Minor Third 6/5 = 1.2000 1.18921 Major Third 5/4 = 1.2500 1.25992 Fourth 4/3 = 1.3333 1.33483 Diminished Fifth 45/32 = 1.4063 1.41421 Fifth 3/2 = 1.5000 1.49831 Minor Sixth 8/5 = 1.6000 1.58740 Major Sixth 5/3 = 1.6667 1.68179 Minor Seventh 9/5 = 1.8000 1.78180 Major Seventh 15/8 = 1.8750 1.88775 Octave 2.0000 2.0000 51 Back for some physics 52