* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PowerPoint
Discrete mathematics wikipedia , lookup
Central limit theorem wikipedia , lookup
Foundations of statistics wikipedia , lookup
Infinite monkey theorem wikipedia , lookup
Inductive probability wikipedia , lookup
Birthday problem wikipedia , lookup
Risk aversion (psychology) wikipedia , lookup
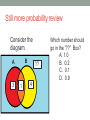
STATISTICS 200 Lecture #13 Tuesday, October 4, 2016 Textbook: Sections 7.3, 7.4, 8.1, 8.2, 8.3 Objectives: • Identify, and resist the temptation to fall for, the “gambler’s fallacy” • Define “random variable” and identify the difference between discrete and continuous. • Use and recognize probability distribution functions (for discrete) or density functions (for continuous) • Calculate and interpret the expected value of a discrete random variable. Confusion of the inverse Suppose that a particular disease affects 1% of those who get tested for it. Also suppose that the test is 98% accurate. What would you advise a patient who tests positive if the test result were the only piece of information? True probability of disease given this information : about 33% Confusion between P(disease present given positive test) and P(positive test given disease present) Cancer testing: confusion of the inverse Suppose we have a cancer test for a certain type of cancer. Sensitivity of the test: If you have cancer then the probability of a positive test is .98. Pr(+ given you have C) = .98 Specificity of the test: If you do not have cancer then the probability of a negative test is .98. Pr(– given you do not have C) = .98 Base rate: The percent of the population who has the cancer. This is the probability that someone has C. Suppose for our example it is 1%. Hence, Pr(C) = .01. Table of proportions (given): + – Base rate C .98 .02 .01 no C .02 .98 .99 Hypothetical table of counts: Pr(C given a positive test result) = 98/296 = 33.1% Gambler’s fallacy • Long-term probabilities should apply in the short term (false!) • Random events should be “selfcorrecting” (false!) Example: a gambler who loses 48 times at a slot machine thinks that he is about to win, since he knows the slot machine pays big 1 in every 50 times in the long run. Law of large numbers (this is true!) If an event is repeated many times independently with the same probability of success each time, the long-run success proportion will approach that probability. • With independent events, knowing what has happened tells you nothing about what will happen. Misunderstanding this leads to the gambler’s fallacy, also known as: The “law of small numbers” (not a real thing), which is that small samples will always be representative of the population from which they are drawn. More on Gambler’s Fallacy Suppose you flip four coins, keeping track of the results in order. • Which is more likely, HHHH or HTTH? • Which is more likely, four total heads or two total heads? Note: These questions are not the same! One of these questions is often mistakenly answered due to belief in the "Law of small numbers" (also known as the Gambler's Fallacy). More probability review Suppose that you roll a fair 6-sided die until the first occurrence of a 4. What is the probability that the first 4 occurs on the third roll? (A) (B) (C) (D) (E) 1/6 5/6 (5/6) × (5/6) × (1/6) (1/6) × (1/6) × (1/6) (1/6) + (1/6) + (1/6) Still more probability review Consider the diagram. B A .3 .1 ?? .4 Which number should go in the “??” Box? A. 1.0 B. 0.2 C. 0.1 D. 0.9 What is a random variable? A random variable is a rule for assigning a numerical value to each outcome of a probability experiment. Example: The number of heads that appear if I toss a nickel, a dime, and a quarter. Capital letters like X or Y denote random variables Let X = number of heads X=1 X=2 X=3 X=0 X=2 X=2 X=1 X=1 Later, we’ll assign a probability to each possible value of X. Examples: Discrete Random Variables Possible values of X Flip 3 coins X= # heads 0, 1, 2, 3 Roll 2 dice X= sum of dots 2, 3, …, 11, 12 Survive Monday X= # cups of coffee 0, 1, 2, …, 10, … Discrete Random Variables Discrete list of distinct values. Typically used when a variable is integer-valued without too many possible choices. choices pdf (Probability distribution function) For example: P(X = 2) = 0.278 If X is the sum of two fair dice when rolled. Examples: Continuous Random Variables Possible values of X Catch the R bus X= time waiting Between 0 and 20, ideally Weigh male firefighter X= his weight Between 150 and 250 Run obstacle course X= time to finish 0 to infinity? Continuous Random Variable Assumes a range of values covering an interval. _____________. May be limited by instrument’s accuracy / decimal points, but still continuous. is this area Find probabilities using a probability density function, which is a curve. Calculate probabilities by finding the area under the curve. • We can’t find probabilities for exact outcomes. • For example: P(X = 2) = 0. • Instead we can find probabilities for a range of values. Coin example: build pdf for X = # heads from 3 coin tosses k P(X=k) 0 1 /8 __ 1 __ / 8 2 __ / 8 3 __ / 8 Total 1 Coin example: build pdf for X = # heads from 3 coin tosses k P(X=k) 0 1 /8 __ 1 3 /8 __ 2 __ / 8 3 __ / 8 Total 1 Coin example: build pdf for X = # heads from 3 coin tosses k P(X=k) 0 1 /8 __ 1 3 /8 __ 2 3 /8 __ 3 __ / 8 Total 1 Coin example: build pdf for X = # heads from 3 coin tosses k P(X=k) 0 1 /8 __ 1 3 /8 __ 2 3 /8 __ 3 1 /8 __ Total 1 Example 2: An example of a probability distribution function (pdf) Let X = number of courses per semester taught by PSU faculty k 0 1 2 3 Total P(X = k) 0.1 0.3 0.4 0.2 1.0 Why is this table a pdf? X = number of courses/semester taught by PSU faculty What is the probability that X is: • exactly 2 classes? k P(X = k) 0 0.1 1 0.3 2 0.4 3 0.2 Total 1.0 • at most 2 classes? • at least 1 class? • more than 1 class? Note: need to be careful at the borders X = number of courses/semester taught by PSU faculty What is the probability that X is: • exactly 2 classes? k P(X = k) 0 0.1 1 0.3 2 0.4 3 0.2 Total 1.0 • at most 2 classes? • at least 1 class? • more than 1 class? Note: need to be careful at the borders X = number of courses/semester taught by PSU faculty What is the probability that X is: • exactly 2 classes? k P(X = k) 0 0.1 1 0.3 2 0.4 3 0.2 Total 1.0 • at most 2 classes? • at least 1 class? • more than 1 class? Note: need to be careful at the borders X = number of courses/semester taught by PSU faculty What is the probability that X is: • exactly 2 classes? k P(X = k) 0 0.1 1 0.3 2 0.4 3 0.2 Total 1.0 • at most 2 classes? • at least 1 class? • more than 1 class? Note: need to be careful at the borders 25 Section 8.3: Expected Value for Any Discrete Random Variable Expected Value of X notation µ:`mu’ Average value in the long run. In other words, mean from an imagined infinite number of observations. When calculated using a pdf: a weighted average 26 Expected Value = Sum of “value × probability” over all possible values Faculty Example: Calculate the Expected Value E(X) k P(X = k) 0 0.1 1 0.3 2 0.4 3 0.2 Total 1.0 X = # courses/semester taught by PSU faculty E(X) = µ = 0×(.1) + 1×(.3) + 2×(.4) + 3×(.2) = 1.7 Interpretation: • The average is 1.7 classes for this population 27 Expected Value Application • Probability that Mary Outcome Win wins a game is 0.01. • If she wins: Lose gets $100 Total • If she loses: pays $5. • X = the amount of E(X) = money Mary will gain Questions: X Value 100 -5 NA Probability 0.01 0.99 1.00 (100)×(.01) + (–5)×(.99 = 1 – 4.95 = –3.95 continuous • Variable X is: discrete • Set up pdf • What is the expected gain for Mary? If you understand today’s lecture… 8.1, 8.7, 8.9, 8.15ab, 8.17, 8.21, 8.25, 8.29, 8.33, 8.37 Objectives: • Identify, and resist the temptation to fall for, the “gambler’s fallacy” • Define “random variable” and identify the difference between discrete and continuous. • Use and recognize probability distribution functions (for discrete) or density functions (for continuous) • Calculate and interpret the expected value of a discrete random variable.