Download PreCalc Ch6.4 - LCMR School District

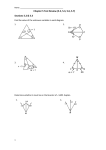
Pre-Calculus Section 6.4- The Law of Sines
Objective: SWBAT use the Law of Sines to solve triangles.
Homework: Page 506 (1-35) odd
Daily Warm Up
1. Simplify
1  hk 1
h 1  k 1
2. The measures of two angles in standard position are given. Determine whether
32 11
,
the angles are coterminal:
3
3
To solve a triangle, we need to know certain information about its sides and angles. In
general, a unique triangle is determined by three of its six parts as long as at least one of
these three parts is a side. The possibilities are as follows:
Case 1 One side and two angles (ASA or SAA)
Case 2 Two sides and the angle opposite one of those sides (SSA)
Case 3 Two sides and the included angle (SAS)
Case 4 Three sides (SSS)
Cases 1 and 2 are solved using the Law of Sines; Cases 3 and 4 require the Law of
Cosines.
The Law of Sines
The Law of Sines says that in any triangle the lengths of the sides are proportional to the
sines of the corresponding opposite angles.
The Law of Sines
In triangle ABC we have
sin A sin B sin C


a
b
c
Proof:
Example 1: Tracking a Satellite (ASA)
A satellite orbiting the earth passes directly overhead at observation stations in
Phoenix and Los Angeles, 340 mi apart. At an instant when the satellite is between these
two stations, its angle of elevation is simultaneously observed to be 60 o at Phoenix and
75o at Los Angeles. How far is the satellite from Los Angeles? In other words, find the
distance AC in the figure below.
C
a
b
75o
A
c  340 mi
Los Angeles
60 o
B
Phoenix
B
Example 2: Solving a Triangle (SAA)
Solve the triangle in the figure.
a
25o
c  80.4
20 o
A
b
C
The Ambiguous Case
In Examples 1 and 2 a unique triangle was determined by the information given.
This is always true of Case 1 (ASA or SAA). But in Case 2 (SSA) there may be two
triangles, one triangle, or no triangle with the given properties. For this reason, Case 2 is
sometimes called the ambiguous case. To see why this is so, we show in the figure the
possibilities when angle A and sides a and b are given. In part (a) no solution is possible,
since side a is too short to complete the triangle. In part (b) the solution is a right
triangle. In part (c) two solutions are possible, and in part (d) there is a unique triangle
with the given properties.
C
a
b
A
C
b
A
(a)
C
ba
a
B
(b)
AB
C
b
a
B
(c)
One-Solution Case (SSA)
Solve triangle ABC, where A  45o , a  7 2 , and b = 7.
a
A
B
(d)
Two-Solution Case (SSA)
Solve triangle ABC if A  43.1o , a  186.2, b  248.6 .
No Solution Case (SSA)
Solve triangle ABC, where A  42o , a  70, b  122 .